算法设计与分析——回溯法——批处理作业调度

我就是我 2023-01-20 11:49 28阅读 0赞

问题描述：给定n个作业的集合\{J1,J2,…,Jn\}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

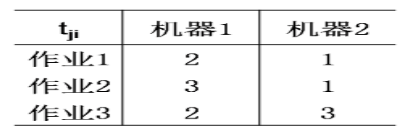
![在这里插入图片描述][2021051222380421.png]

这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

以1,2,3为例:  
作业1在机器1上完成的时间为2,在机器2上完成的时间为3  
作业2在机器1上完成的时间为5,在机器2上完成的时间为6  
作业3在机器1上完成的时间为7,在机器2上完成的时间为10  
3+6+10=19，所以时间和为19。

以1,3,2为例:  
作业1在机器1上完成的时间为2,在机器2上完成的时间为3  
作业3在机器1上完成的时间为4,在机器2上完成的时间为7  
作业2在机器1上完成的时间为7,在机器2上完成的时间为8  
3+7+8=18，所以时间和为18。

批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度，所以如图，批处理作业调度问题的解空间是一颗排列树。按照回溯法搜索排列树的算法框架，设开始时x=\[1,2,……n\]是所给的n个作业，则相应的排列树由x\[1:n\]的所有排列构成。

算法分析：  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70]

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70 1]

#include<iostream>
    
    #include<stdlib.h>
    using namespace std;
    class Flowshop
    {
        
    	public:
    		int **M;//各作业需要的处理时间 
    		int *x;//当前作业调度 
    		int *bestx;//当前最优作业调度 
    		int *f2;//机器2完成处理时间 
    		int f1;//机器1完成处理时间 
    		int f;//完成时间和 
    		int bestf;//当前最优值 
    		int n;//作业数量 
    	void Backtrack(int i);//回溯算法 
    	
    };
    
    
    
    void Flowshop::Backtrack(int i)
    {
        
    	if(i>n)
    	{
        
    		for(int i=1;i<=n;i++)//记录路径 
    		{
        
    			bestx[i]=x[i];
    		}
    		bestf = f;//因为到了叶子结点了，不需要判断了 
    	}
    	else
    	{
        
    		for(int j=i;j<=n;j++)//分枝数 
    		{
        
    		//设置作业在机器1完成的时间
    			f1 +=M[x[j]][1];//回溯算法的关键 
    			f2[i]=((f2[i-1]>f1)? f2[i-1]:f1) +M[x[j]][2];
    			
    			f+=f2[i];//回溯算法的关键 
    			if(f<bestf)
    			{
        
    				swap(x[i],x[j]);
    				Backtrack(i+1);
    				swap(x[i],x[j]);
    			}
    			f1 -=M[x[j]][1];//回溯算法的关键 
    			f -=f2[i];//回溯算法的关键 
    			 
    			
    		 } 
    	} 
     } 
    
    int Flow(int **M,int n,int bestx[])//初始化 
    {
        
    	int ub = INT_MAX;
    	Flowshop X;
    	X.x = new int [n+1];
    	X.f2 = new int [n+1];
    	X.M=M;
    	X.n=n;
    	X.bestx=bestx;
    	X.bestf = ub;
    	X.f1 = 0;
    	X.f = 0;
    	for(int i=0;i<=n;i++)
    	{
        
    		X.f2[i]=0,X.x[i]=i;
    		
    	}
    	X.Backtrack(1);
    	delete[] X.x;
    	delete[] X.f2;
    	return X.bestf;
    }
    int main()
    {
        
    	int n;
    
    	cout<<"请输入要处理作业的数量：";
    	cin>>n;
    	int bestx[n+1];
        int **M =new int *[n+1];
        for(int i=0;i<n+1;i++)
        {
        
        	M[i]= new int [3];
    	}
    	cout<<"请输入每个作业在两个机器上工作的处理时间序列:(如1 2)："<<endl; 
    	for(int i=1;i<=n;i++)
    	{
        
    		cin>>M[i][1]>>M[i][2];
    	}
    	cout<<"所有作业在机器2上的完成时间和(该作业调度的完成时间)为："<<Flow(M,n,bestx);
    }

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70 2]  
算法的时间复杂度为O(n!)

[2021051222380421.png]: /images/20221021/7b7596d2dc304079a413e0a9ae26056c.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70]: /images/20221021/451a93f841274912aa2a5e8bccedaa63.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70 1]: /images/20221021/55093a72f28d4e4db82d67d4e08a5402.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzUwNjc1ODEz_size_16_color_FFFFFF_t_70 2]: /images/20221021/1af837a6464a46d7b19a80bc5e561a42.png