计算机组成原理——浮点数加减运算&强制类型转换

亦凉 2023-01-21 02:11 152阅读 0赞

文章目录

  • 浮点数的加减运算
    • 十进制浮点数加减运算步骤：
    • 二进制浮点数的加减运算
        1. 对阶
        1. 尾数加减
        1. 规格化
        1. 舍入
        1. 判溢出
    • 浮点数的加减运算——舍入规则
      • “0”舍“1”入法：
      • 恒置“1”法：
  • 强制类型转换
      • 转化的可操作性

浮点数的加减运算

我们可以先通过十进制的浮点数加减运算步骤来类推二进制的

十进制浮点数加减运算步骤：

浮点数加减运算包括五个步骤：① 对阶② 尾数加减③ 规格化④ 舍入⑤ 判溢出

例如：计算9.85211 × 1012 + 9.96007 × 1010

解：在这里插入图片描述

二进制浮点数的加减运算

上面我们进行了十进制的浮点数的加减运算，下面我们可以以此类推，也按照上面五个步骤来做

直接看一个例题：已知十进制数X=−5/256、Y=+59/1024，按机器补码浮点运算规则计算X−Y，结果用二进制表示，浮点数格式如下：阶符取2位，阶码取3位，数符取2位，尾数取9位

解：

首先我们先用补码表示阶码和尾数，

5D = 101B，1/256 = 2-8 → X = - 101 × 2-8 = - 0.101 × 2-5 = - 0.101 × 2-101
59D = 111011B，1/1024 = 2-10 → Y = + 111011 × 2-10 = + 0.111011 × 2-4 = + 0.111011 × 2-100

再转化成补码形式
X：11011,11.011000000
（X是负数 转化成补码取反+1 阶码 尾数都一样操作）
Y：11100,00.111011000

1. 对阶

使两个数的阶码相等，小阶向大阶看齐，尾数毎右移一位，阶码加1

① 求阶差：[ΔE]补=11011+00100=11111，知ΔE=−1
② 对阶：
X：11011,11.011000000 → 11100,11. 101100000
X = - 0.0101 × 2-100

2. 尾数加减

-Y：11100,11.000101000
（求码的负数的方法：连符号位一块取反+1）

然后让X加上-Y

  1. 11.101100000
  2. +     11.000101000
  3.     10.110001000

所以X-Y：11100, 10.110001000

3. 规格化

X-Y：11100, 10.110001000 à 11101,11.011000100

4. 舍入

无舍入

5. 判溢出

常阶码，无溢出，结果真值为2−3×(−0.1001111)2

浮点数的加减运算——舍入规则

“0”舍“1”入法：

类似于十进制数运算中的“四舍五入”法，即在尾数右移时，被移去的最高数值位为0，则舍去；被移去的最高数值位为1，则在尾数的末位加1。这样做可能会使尾数又溢出，此时需再做一次右规。

恒置“1”法：

尾数右移时，不论丢掉的最高数值位是“1”还是“0”，都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能。

例如
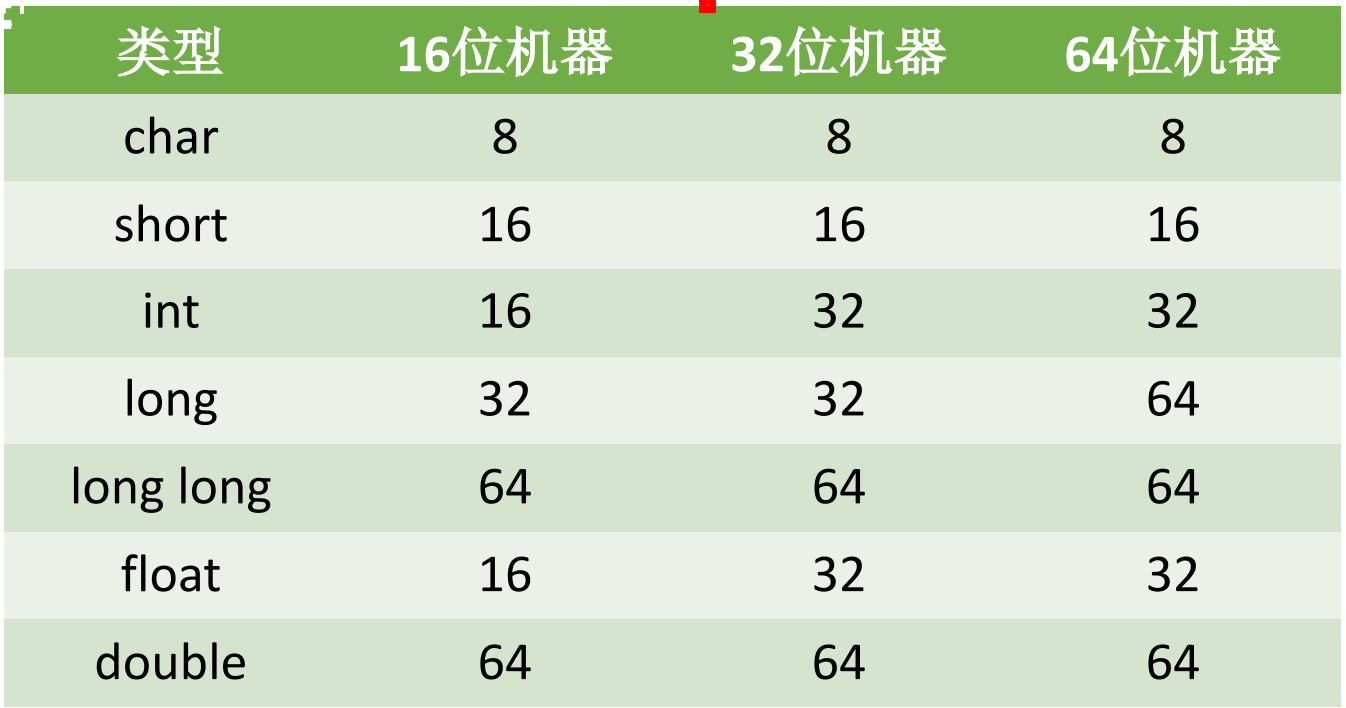
在这里插入图片描述

强制类型转换

在这里插入图片描述

转化的可操作性

char → int → long → double
float → double
int → float：可能损失精度
float → int：可能溢出及损失精度

结论：范围、精度从小到大，转换过程没有损失

原因：拿32位来说：
int：表示整数，范围 -231 ～ 231-1 ，有效数字32位
float：表示整数及小数，范围 ±[2-126 ～ 2127×(2−2−23)]，有效数字23+1=24位

发表评论

表情：
评论列表 （有 0 条评论，152人围观）

还没有评论，来说两句吧...

相关阅读

    相关 浮点数运算

    今天学习了浮点数运算（加减乘除）。浮点数运算主要包括两部分：指数运算和尾数运算。在IEEE754标准下，指数运算就是阶码的运算，类似于无符号数运算。尾数运算是原码运算。之前一直

    短命女短命女/ 0 赞/ 215 阅读