ResNet:Deep Residual Learning for Image Recognition
ResNet:Deep Residual Learning for Image Recognition
文章目录
- ResNet:Deep Residual Learning for Image Recognition
- 参考
- 网络退化问题
- 残差结构
- ResNet理论
- 网络结构
- 训练设置
- 其他ResNet结构
- ResNet的效果
- ResNet的极限深度
参考
- 1、你必须要知道CNN模型：ResNet
- 2、ResNet论文详解
- 3、Caffe Scale层解析
- 4、深度学习网络结构中超参数momentum了解
网络退化问题
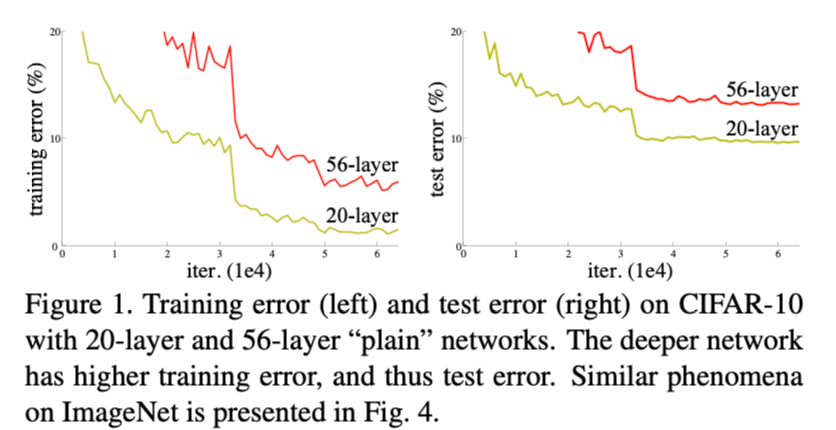
- 卷积网络在深度堆叠（一定的深度后）的同时，其精度并没有随之上升。如上图所示，56-layer的网络的error比20-layer的高，training和testing都是如此，说明这个不是由过拟合导致的，而是网络的退化，并且在适当的深度模型上添加更多的层会导致更高的训练误差。
网络层数堆叠的缺点：
- 1.网络难以收敛，梯度消失/爆炸在一开始就阻碍网络的收敛。
- 2.当更深的网络能够开始收敛时，暴露了一个退化问题：随着网络深度的增加，准确率达到饱和然后迅速下降。
残差结构
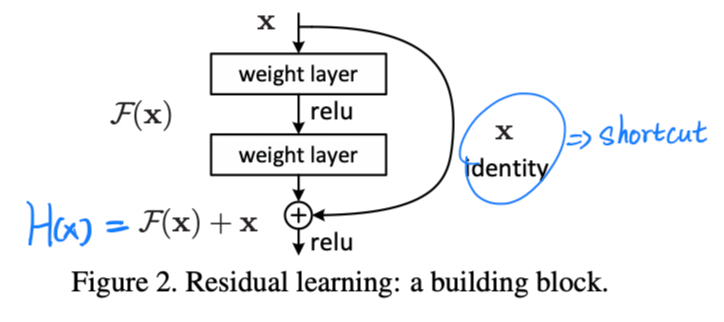
这是论文中的残差结构，其中H(x)为观察值，F(x)就是残差输出，F(x)=H(x)-x
由于我这两天搞了个ResNet50版的R2CNN的模型，就以此为例
- 用的卷积块一般由以下几部分组成：conv层、BN层、Scale层（参考链接3，在pytorch中属于BN的一部分，主要用于权重缩放和偏移）、ReLU
- 其中卷积块的kernel size一般为131的组合，当kernel size=3的时候，pad=1，如此保持特征图前两维大小不变
- 左路的卷积块为1x1卷积，在改变输出channel时候用于input的channel转换（如果channel数和输出一致，则不用这个，这个也就是残差的两种计算方式）
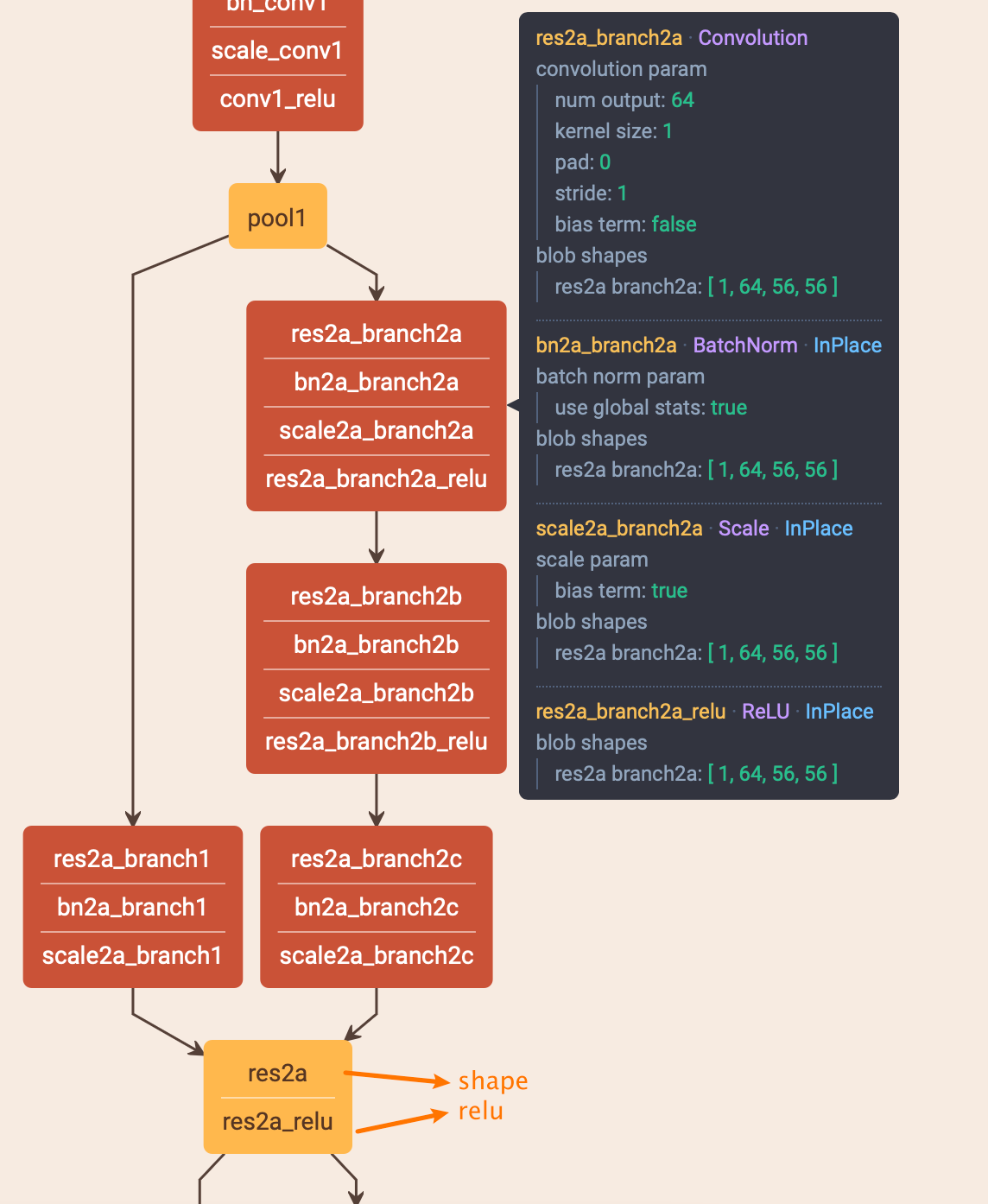
ResNet理论
残差结构确实比其他结构更易学习
- 如果添加的层可以被构建为恒等映射，更深模型的训练误差应该不大于它对应的更浅版本。退化问题表明求解器通过多个非线性层来近似恒等映射可能有困难。通过残差学习的重构，如果恒等映射是最优的，求解器可能简单地将多个非线性连接的权重推向零来接近恒等映射。
- 在实际情况下，恒等映射不太可能是最优的，但是残差可能有助于对问题进行预处理。如果最优函数比零映射更接近于恒等映射，则求解器应该更容易找到关于恒等映射的抖动，而不是将该函数作为新函数来学习。
- 对于不用channel变换的残差块，公式采用：
y = F ( x , { W i } ) + x y = F(x,\{W_i\})+x y=F(x,{ Wi})+x
- 这里的y就是上面的H(x)，F就是残差,σ是ReLU函数，实际上也就是两个卷积层的运算，对于它为什么叫做残差运算，我个人目前的理解是：先残差结构整块看成黑盒，然后输出理论上就是几个卷积的正常输出，只不过占比不同了，由于还要加上input，F的占比从100%下降为50%，因此相对于整体输出（即H(x)）是残差的
F = W 2 σ ( W 1 x ) F = W_2σ(W_1x) F=W2σ(W1x)
- 对于需要channel变换残差块，公式采用：
y = F ( x , { W i } ) + W s x y = F(x,\{W_i\})+W_sx y=F(x,{ Wi})+Wsx
- 基本上就是把原来的x用1x1卷积变换下channel数，然后和残差输出相加
网络结构
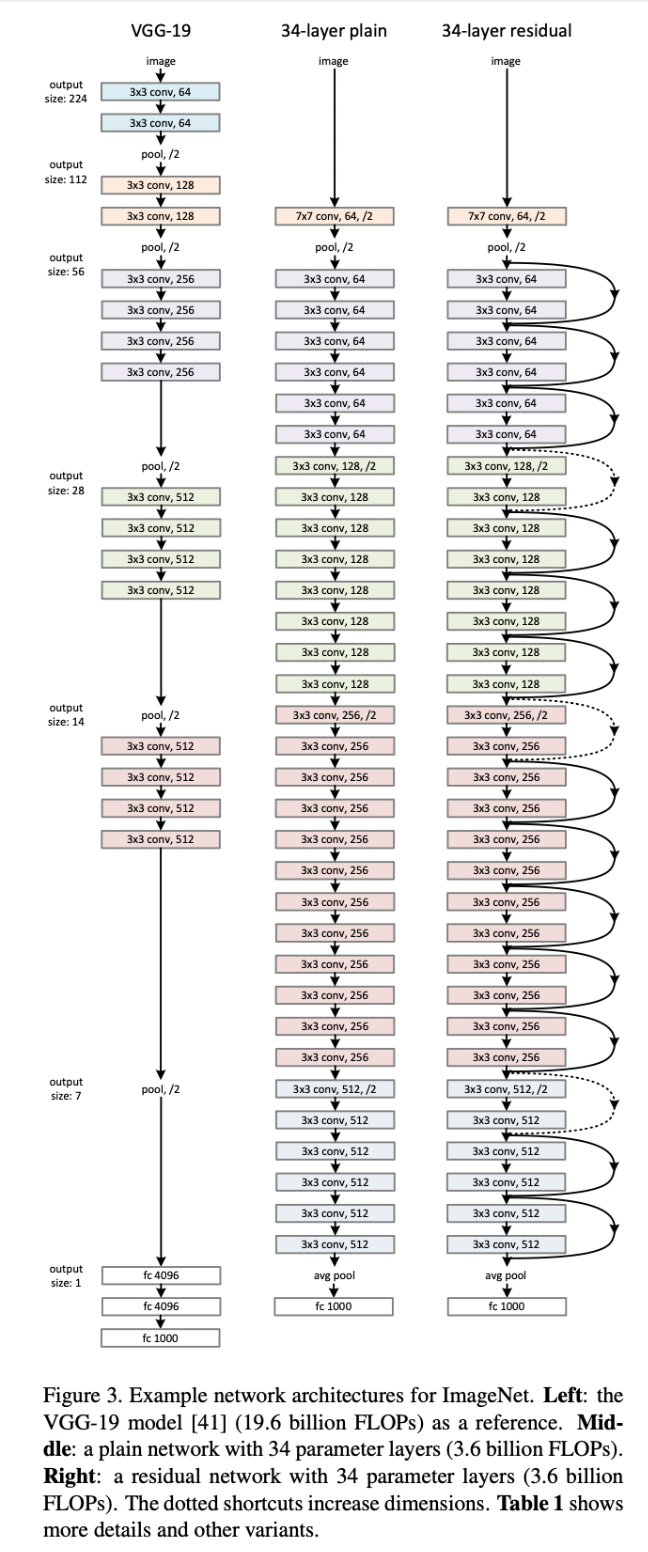
ResNet整体参考了VGGnet（我觉得指的是参考了卷积层kernel为3这个设定），下图左侧是VGG19，右侧是resnet-34，中间是34层不带残差的网络
训练设置
- 输入：224x224
- 标准色彩增强
- BN层
- 优化器：SGD
- 学习率从0.1开始，当误差稳定时除以10
- 训练600000个iter
- 权重衰减为0.0001，动量（momentum，见参考链接4）为0.9
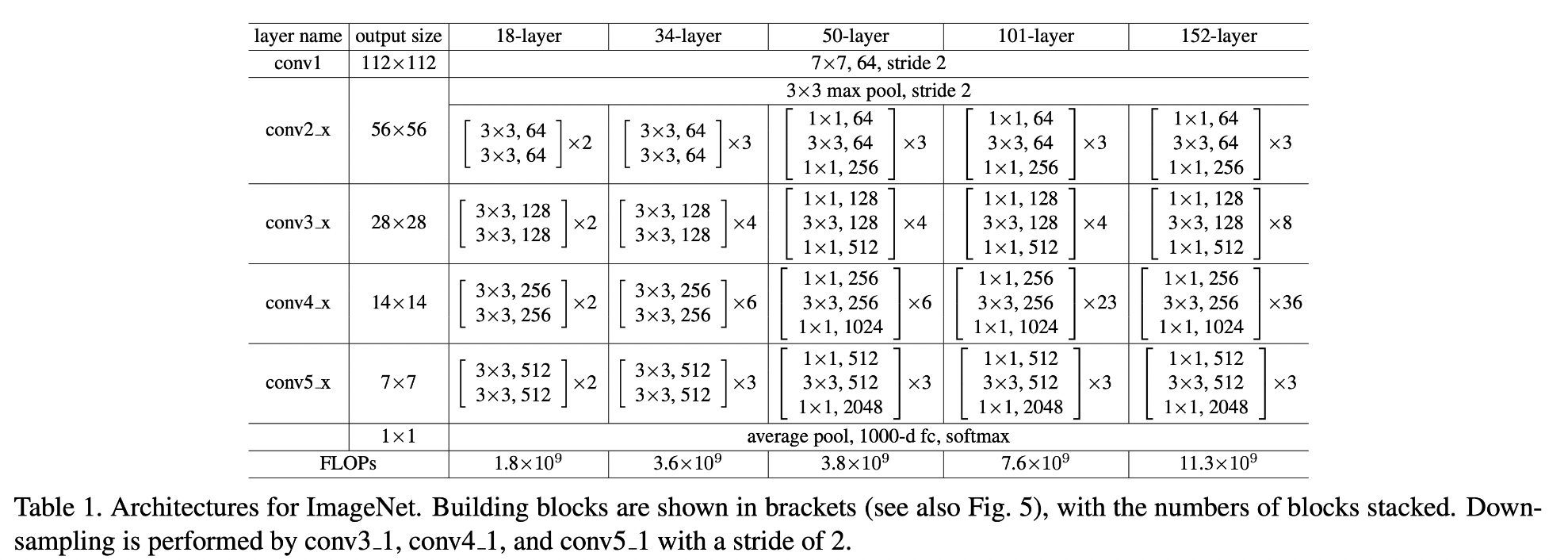
其他ResNet结构
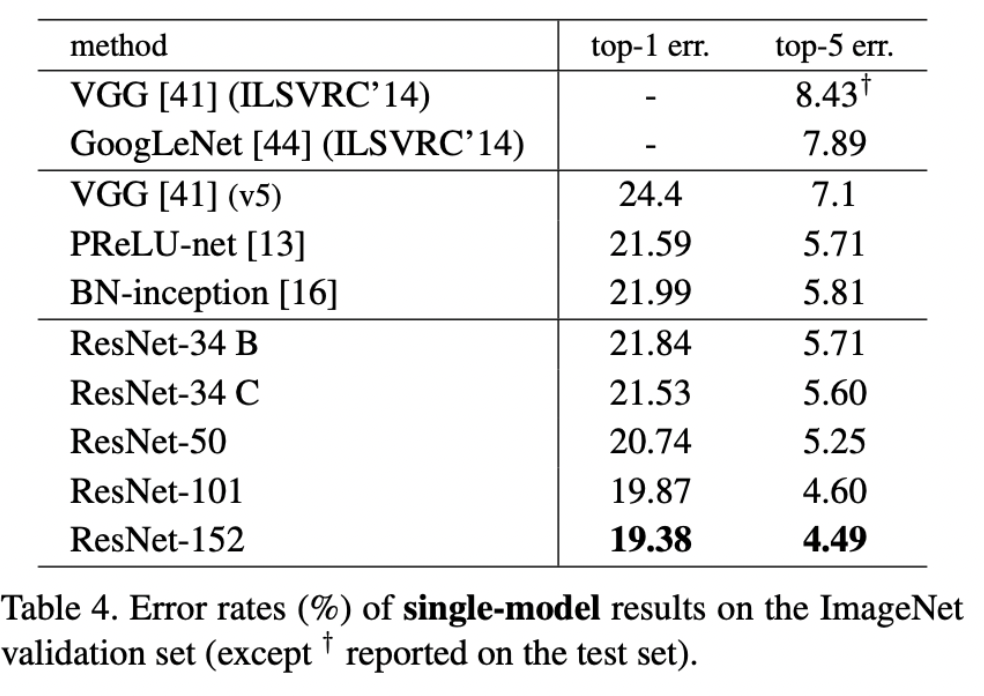
ResNet的效果
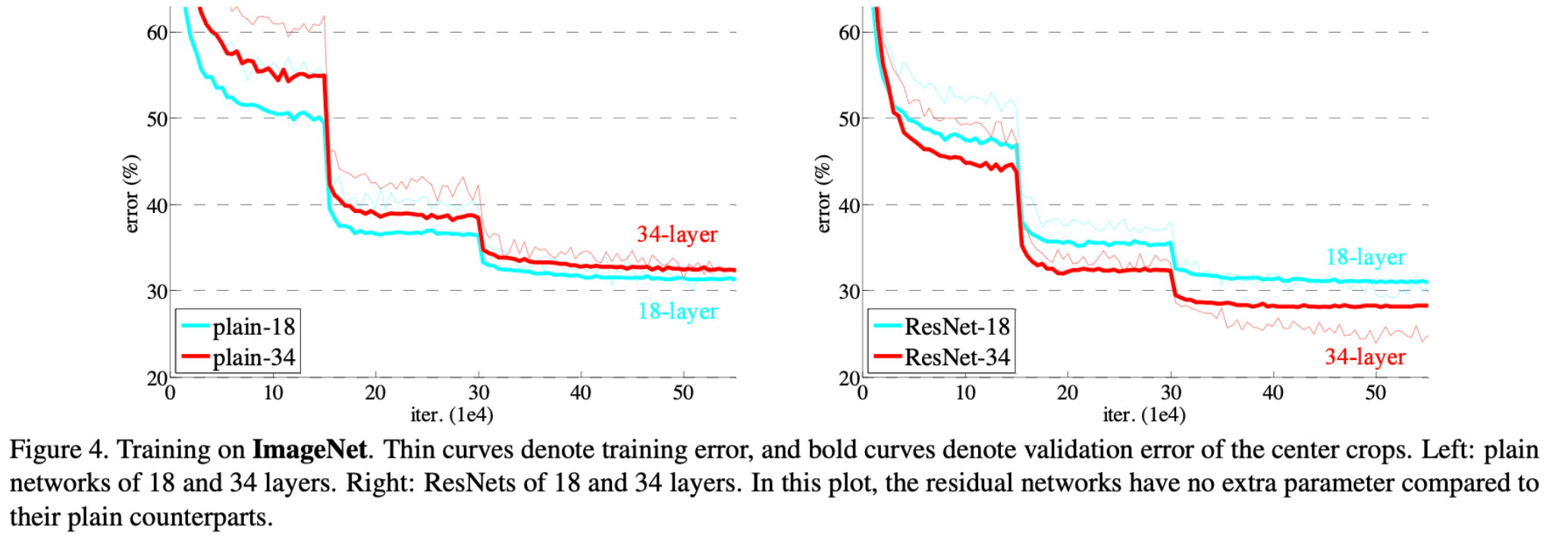
- 从这张图中的对比可以知道，残差结构可以有效缓解网络退化的问题，是的更深的网络（34-layer）的错误率更低
ResNet的极限深度
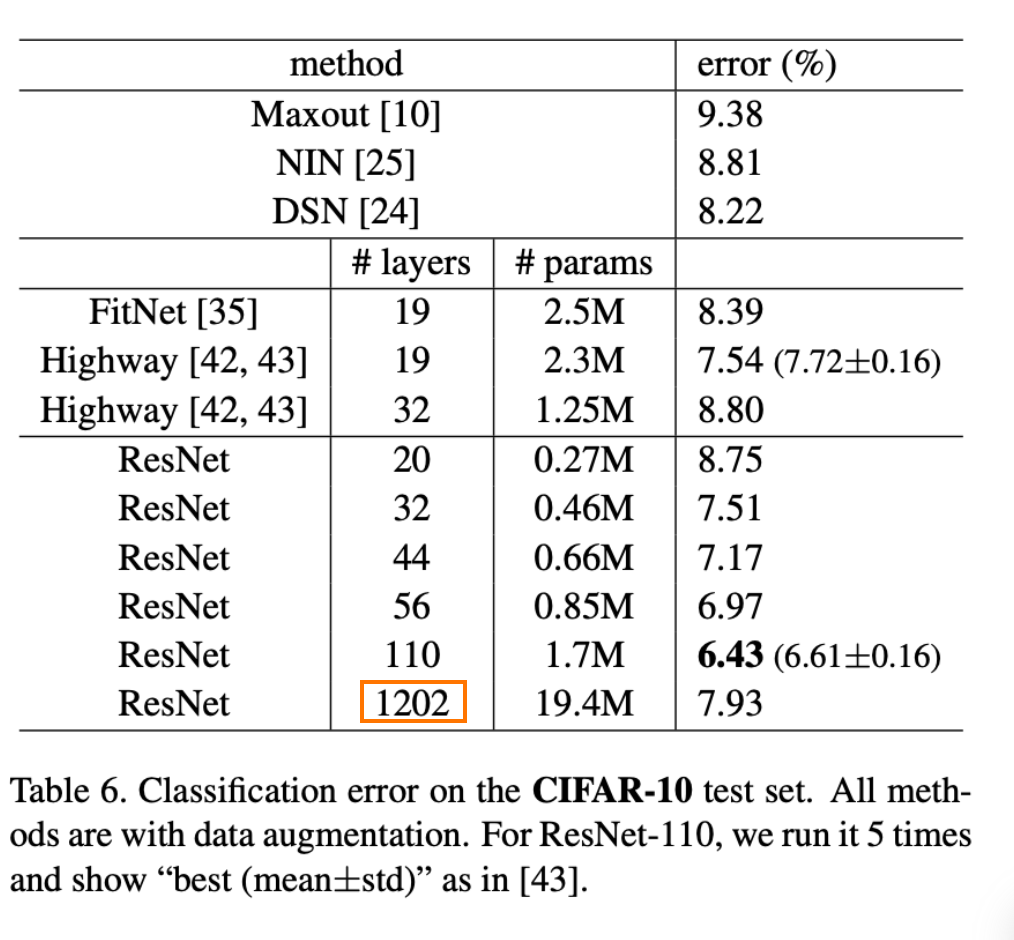
- 下图中的ResNet在层数达到1000层的时候还是出现了退化现象，根据作者的实验，152层已经接近该版本ResNet的极限层数了
刺骨的言语ヽ痛彻心扉
朱雀
太过爱你忘了你带给我的痛
Bertha 。
秒速五厘米
我就是我
还没有评论，来说两句吧...