数据结构笔记——由遍历序列构造二叉树

た 入场券 2023-02-13 08:05 97阅读 0赞

目录

一、不同二叉树的中序遍历序列

二、前序+中序遍历序列

三、后序+中序遍历序列

四、层序+中序遍历序列

五、若前序、后序、层序序列两两组合？

六、总结

一、不同二叉树的中序遍历序列

中序遍历：中序遍历左子树、根结点、中序遍历右子树

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70

前序遍历：根结点、前序遍历左子树、前序遍历右子树

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 1

后序遍历：前序遍历左子树、前序遍历右子树、根结点

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 2

结论：若只给出一棵二叉树的前、中、后、层序遍历序列中的一种，不能唯一确定一棵二叉树

20200527215552929.png

二、前序+中序遍历序列

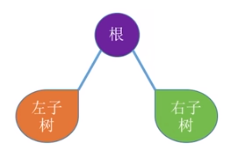
20200527215840965.png

前序遍历序列：根结点 左子树的前序遍历序列 右子树的前序遍历序列

中序遍历序列：左子树的中序遍历序列 根结点 右子树的中序遍历序列

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 3

例1：

20200527220032422.png

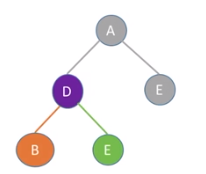
20200527220055298.png

例2：

20200527220308142.png

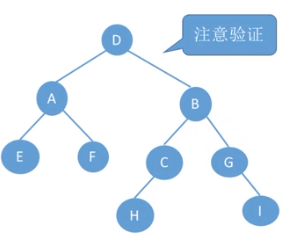
20200527220324436.png

三、后序+中序遍历序列

后序遍历序列：左子树的中序遍历序列 右子树的中序遍历序列 根结点

中序遍历序列：左子树的中序遍历序列 根结点 右子树的中序遍历序列

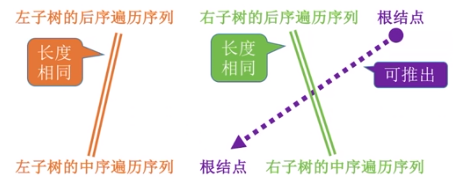
20200527220445868.png

例：

20200527220458525.png

20200527220324436.png

四、层序+中序遍历序列

层序遍历序列：根结点 左子树的根右子树的根

中序遍历序列：左子树的中序遍历序列 根结点 右子树的中序遍历序列

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 4

例1：

20200527220742792.png

20200527220324436.png

例2：

20200527220928530.png

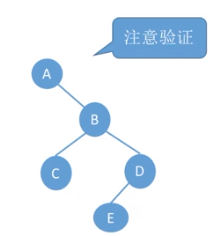
20200527220946384.png

五、若前序、后序、层序序列两两组合？

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 5

六、总结

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwMzEwMTQ4_size_16_color_FFFFFF_t_70 6

发表评论

表情：
评论列表 （有 0 条评论，97人围观）

还没有评论，来说两句吧...

相关阅读

    相关 数据结构——树——二叉树遍历

    遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质

    r囧r小猫r囧r小猫/ 0 赞/ 413 阅读