算法-除自身以外数组的乘积
算法-除自身以外数组的乘积
1 题目概述
1.1 题目出处
https://leetcode-cn.com/problems/product-of-array-except-self/
1.2 题目描述
给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
提示:题目数据保证数组之中任意元素的全部前缀元素和后缀(甚至是整个数组)的乘积都在 32 位整数范围内。
说明: 请不要使用除法,且在 O(n) 时间复杂度内完成此题。
进阶:
你可以在常数空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组不被视为额外空间。)
2 循环+记忆缓存
2.1 思路
直接循环遍历,出去当前遍历数,将其他数相乘得到结果,且放入该数字对应的Map-Entry中缓存。下次遇到同样数字时可直接取出得到结果,不再重复计算。
2.2 代码
class Solution {public int[] productExceptSelf(int[] nums) {int[] output = new int[nums.length];Map<Integer, Integer> cache = new HashMap<>();for(int i = 0; i < nums.length; i++){Integer result = cache.get(nums[i]);if(null != result){output[i] = result;continue;}output[i] = 1;for(int j = 0; j < nums.length; j++){if(j == i){continue;}output[i] *= nums[j];}cache.put(nums[i], output[i]);}return output;}}
2.3 时间复杂度

最坏情况数字都不相同,无法使用缓存,此时为O(N^2)。
不符合O(N)
2.4 空间复杂度
O(N)
3 两趟遍历记录当前数之前的数和之和的数乘积
3.1 思路
题目要求在O(N)时间内完成,且额外空间复杂度为1。那么就想到将所有数字相乘,遍历每个数字时除以该数字即可。但又要求不能做除法?那咋搞?
首先想到位运算,但因不适合除了2的倍数以外的计算,作罢。
还有什么小学时学的除法公式,也不能在O(1)时间复杂度计算出来,排除掉。
难道就就没有办法了吗?
再想想题目,是求所有数的乘积,除去当前遍历位置的,也就是说只要我记录下这个数之前和之后的数的乘积不就行了吗?
到这里你肯定要说,我都没算后面的我咋知道当前遍历数字后面数的乘积呢?那我们就两趟遍历呗,正着一趟、反着一趟不就行了吗?
3.2 代码
可修改原数组nums的代码:
class Solution {
public int[] productExceptSelf(int[] nums) {int[] output = new int[nums.length];output[0] = 1;for(int i = 1; i < nums.length; i++){// 首趟遍历,存下之前的数的乘积,即不选当前i的乘积// 注意,这里output[i - 1]表示不选i-1的数的乘积// 所以还需要乘i-1output[i] = output[i - 1] * nums[i - 1];}// 第二趟遍历,将每个nums[i]用来保存包括当前数字及后续所有数字的乘积for(int i = nums.length - 2; i >= 0; i--){// i前面的数以及不包括当前数i的乘积 * i后面所有数的乘积output[i] *= nums[i + 1];// nums[i]用来保存包括当前数字及后续所有数字的乘积nums[i] *= nums[i + 1];}return output;}
}
不修改原数组nums代码:
class Solution {
public int[] productExceptSelf(int[] nums) {int[] output = new int[nums.length];output[0] = 1;for(int i = 1; i < nums.length; i++){// 首趟遍历,存下之前的数的乘积,即不选当前i的乘积// 注意,这里output[i - 1]表示不选i-1的数的乘积// 所以还需要乘i-1output[i] = output[i - 1] * nums[i - 1];}int total = 1;// 第二趟遍历,设一个变量保存包括当前数字及后续所有数字的乘积for(int i = nums.length - 1; i >= 0; i--){// i前面的数以及不包括当前数i的乘积 * i后面所有数的乘积output[i] *= total;// 更新当前数字及后续所有数字的乘积total *= nums[i];}return output;}
}
3.3 时间复杂度
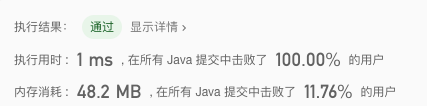
3.4 空间复杂度
O(1)

































还没有评论,来说两句吧...