图：深度优先遍历&广度优先遍历

左手的ㄟ右手 2023-02-28 01:26 143阅读 0赞

1，图的基本概念

1.1，图的基本介绍

  • 线性表局限于一个直接前驱和一个直接后继的关系
  • 树也只能有一个直接前驱也就是父节点
  • 当需要多对多的关系的时候，就应该用到图

1.2，图的常用概念

  • 顶点（Vertex）
  • 边（Edge）
  • 路径
  • 无向图
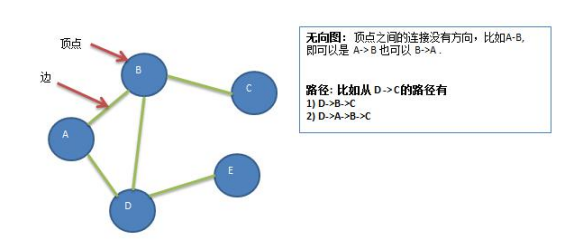
    在这里插入图片描述
  • 有向图
  • 带权图
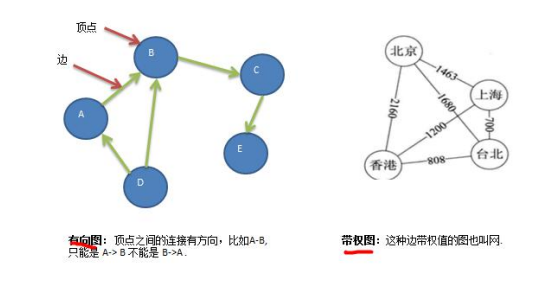
    在这里插入图片描述

1.3，图的表达方式

  • 图的表示方式有两张：二维数组表示（邻接矩阵），链表表示（邻接表）
  • 邻接矩阵：是表示图形中顶点之间相邻关系的矩阵，对于N个顶点的图而言，矩阵的row和column分别表示n个点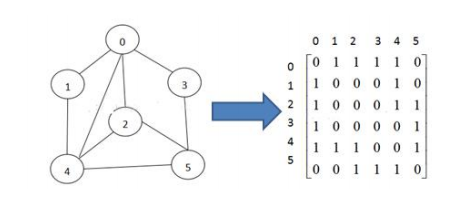
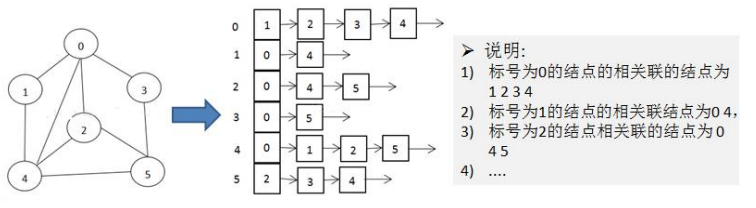
    在这里插入图片描述

  • 邻接表

    • 邻接矩阵需要为每个顶点分配n个边的空间，但是其实很多边在图中不存在，会造成额外的空间浪费
    • 邻接表的实现只关心存在的边，不关心不存在的边，不存在空间浪费，邻接表由数组和链表组成
      在这里插入图片描述

2，图的深度优先遍历

2.1，基本思想

  • 深度优先遍历，从初始访问节点出发，首先访问它的第一个邻接节点；然后以该邻接节点作为初始节点，继续访问它的第一个邻接节点；以此类推
  • 如果第一个邻接节点不存在或者已经递归遍历完成，则获取第二个邻接节点作为初始节点
  • 由此可以看到，深度优先遍历是先向纵深挖掘遍历，纵深遍历完成后，再进行横向遍历
  • 显示，深度优先遍历时一个递归的过程

2.2，算法步骤

  1. 访问初始节点index，并将该节点标记为已访问
  2. 查找初始节点index的第一个邻接节点nextIndex
  3. 若nextIndex存在，则继续执行第四步；若nextIndex不存在，则退回第二步，继续查找index的下一个邻接节点，继续进行第三步判断
  4. 若nextIndex未被访问，则对nextIndex进行深度优先遍历，即从第一步递归
  5. 若nextIndex已经被访问，则回到第二步，继续查找index的下一个临界点，继续判断

2.3，代码实现

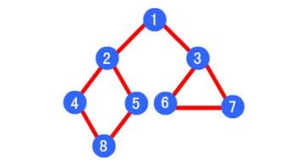
在这里插入图片描述

  • 深度优先遍历结果为：1 -> 2 -> 4 -> 8 -> 5 -> 3 -> 6 -> 7

    package com.self.datastructure.chart;

    import org.apache.commons.collections.CollectionUtils;

    import java.util.ArrayList;
    import java.util.Arrays;
    import java.util.LinkedList;
    import java.util.List;

    / 图基本入门 @author PJ_ZHANG @create 2020-04-20 16:16 /
    public class QuickStartChart { 

    1. public static void main(String[] args) { 
    2.     MyChart myChart = createChart(8);
    3.     System.out.println("深度优先遍历: ");
    4.     myChart.dfs();
    5. }
    7. /** * 创建图 * @param vertexNum 顶点数量 * @return */
    8. private static MyChart createChart(int vertexNum) { 
    9.     MyChart myChart = new MyChart(vertexNum);
    10.     for (int i = 1; i <= vertexNum; i++) { 
    11.         myChart.addVertex(String.valueOf(i));
    12.     }
    13.     myChart.addEdge(myChart.indexOf("1"), myChart.indexOf("2"), 1);
    14.     myChart.addEdge(myChart.indexOf("1"), myChart.indexOf("3"), 1);
    15.     myChart.addEdge(myChart.indexOf("2"), myChart.indexOf("4"), 1);
    16.     myChart.addEdge(myChart.indexOf("2"), myChart.indexOf("5"), 1);
    17.     myChart.addEdge(myChart.indexOf("3"), myChart.indexOf("6"), 1);
    18.     myChart.addEdge(myChart.indexOf("3"), myChart.indexOf("7"), 1);
    19.     myChart.addEdge(myChart.indexOf("4"), myChart.indexOf("8"), 1);
    20.     myChart.addEdge(myChart.indexOf("5"), myChart.indexOf("8"), 1);
    21.     return myChart;
    22. }
    24. /** * 自定义图类进行处理 */
    25. static class MyChart { 
    27.     /** * 顶点数量 */
    28.     private int vertexNum;
    30.     /** * 顶点列表 */
    31.     private List<String> lstVertex;
    33.     /** * 顶点路径 */
    34.     private int[][] vertexPathArray;
    36.     /** * 边数量 */
    37.     private int edgeNum;
    39.     /** * 是否已经被访问 */
    40.     private boolean[] isVisited;
    42.     MyChart(int vertexNum) { 
    43.         this.vertexNum = vertexNum;
    44.         lstVertex = new ArrayList<>(vertexNum);
    45.         vertexPathArray = new int[vertexNum][vertexNum];
    46.         isVisited = new boolean[vertexNum];
    47.     }
    49.     /** * 添加顶点, 此处不涉及扩容 * * @param vertex 添加的顶点 */
    50.     void addVertex(String vertex) { 
    51.         if (vertexNum == lstVertex.size()) { 
    52.             throw new ArrayIndexOutOfBoundsException("数组已满");
    53.         }
    54.         lstVertex.add(vertex);
    55.     }
    57.     /** * 添加多个顶点 * * @param vertexArr 顶点数组, 可变参数 */
    58.     void addAllVertex(String ... vertexArr) { 
    59.         if (vertexNum < lstVertex.size() + vertexArr.length) { 
    60.             throw new ArrayIndexOutOfBoundsException("数组已满");
    61.         }
    62.         lstVertex.addAll(Arrays.asList(vertexArr));
    63.     }
    65.     /** * 返回顶点所在的下标 * * @param vertex 目标顶点 * @return 返回下标 */
    66.     int indexOf(String vertex) { 
    67.         return lstVertex.indexOf(vertex);
    68.     }
    70.     /** * 添加边 * * @param xIndex 横坐标 * @param yIndex 纵坐标 * @param weight 边的权重 */
    71.     void addEdge(int xIndex, int yIndex, int weight) { 
    72.         if (xIndex >= vertexNum || yIndex >= vertexNum) { 
    73.             throw new IndexOutOfBoundsException("索引越界");
    74.         }
    75.         vertexPathArray[xIndex][yIndex] = weight;
    76.         vertexPathArray[yIndex][xIndex] = weight;
    77.         edgeNum++;
    78.     }
    80.     /** * 获取边数量 * * @return 返回边数量 */
    81.     int getEdgeNum() { 
    82.         return edgeNum;
    83.     }
    85.     /** * 展示图 */
    86.     void showChart() { 
    87.         for (int[] array : vertexPathArray) { 
    88.             System.out.println(Arrays.toString(array));
    89.         }
    90.     }
    92.     /** * 深度优先遍历 * 从第一个顶点开始进行遍历, 遍历过的顶点标记为已经遍历 * 先获取遍历该顶点的下一个邻接顶点 * 如果不存在, 则继续第二个未遍历顶点开始 * 如果存在, 判断该邻接顶点是否已经遍历过 * 如果没有遍历过, 则继续深度遍历该顶点(递归) * 如果已经遍历过, 则继续寻找下一个邻接顶点 */
    93.     void dfs() { 
    94.         for (int i = 0; i < lstVertex.size(); i++) { 
    95.             // 从第一个节点开始进行遍历
    96.             // 先访问初始节点
    97.             if (!isVisited[i]) { 
    98.                 dfs(i);
    99.             }
    100.         }
    101.     }
    103.     private void dfs(int index) { 
    104.         // 输出当前遍历的节点, 并标记为已访问
    105.         System.out.print(lstVertex.get(index) + " -> ");
    106.         isVisited[index] = true;
    107.         // 获取它的第一个邻接节点进行访问
    108.         int nextIndex = getFirstNeighbor(index);
    109.         // 不等于-1说明存在下一个节点, 继续进行处理
    110.         // 如果等于-1, 说明此次遍历结束, 交由主函数进行下一个节点遍历
    111.         while (nextIndex != -1) { 
    112.             if (!isVisited[nextIndex]) { 
    113.                 // 如果没有被访问, 则继续深度循环遍历进行处理
    114.                 dfs(nextIndex);
    115.             }
    116.             // 如果已经被访问了, 则查找nextIndex的下一个临界节点
    117.             nextIndex = getNextNeighbor(index, nextIndex);
    118.         }
    119.     }
    121.     /** * 获取下一个邻接节点 * X, Y轴已知, 查找Y轴后面第一个存在权值的节点 * @param index * @param nextIndex * @return */
    122.     private int getNextNeighbor(int index, int nextIndex) { 
    123.         for (int i = nextIndex + 1; i < lstVertex.size(); i++) { 
    124.             if (vertexPathArray[index][i] > 0) { 
    125.                 return i;
    126.             }
    127.         }
    128.         return -1;
    129.     }
    131.     /** * 获取第一个邻接节点 * X轴已知, 获取Y轴上第一个存在权值的节点 * @param index * @return */
    132.     private int getFirstNeighbor(int index) { 
    133.         // 在该行坐标轴上进行遍历查找
    134.         // 如果对应坐标的权值大于0, 说明这两个点是有关联关系的
    135.         // 直接返回该点对应的下标索引
    136.         for (int i = 0; i < lstVertex.size(); i++) { 
    137.             if (vertexPathArray[index][i] > 0) { 
    138.                 return i;
    139.             }
    140.         }
    141.         // 如果没有找到, 直接返回-1
    142.         return -1;
    143.     }
    145. }

    }

3，图的广度优先遍历

3.1，基本思想

  • 广度优先遍历，类似于分层搜索的过程；广度优先遍历需要使用一个队列来保持访问过的节点的顺序，以便按照这个顺序来访问这些节点的邻接节点

3.2，算法步骤

  1. 访问初始节点index并标记为已访问
  2. 节点index入队列，相对于深度遍历，广度遍历需要维护一个局部队列

  3. 当队列不为空时，继续遍历执行，否则算法结束

    • 对于刚开始遍历，起步会入index到队列，所以对于第一次必为真
    • 后续操作中，每遍历到一个未访问的节点，都会将该节点入队列，在每一次队列遍历时，移除第一个节点进行广度遍历，等队列最终为空，说明以该节点为初始节点的遍历完成
  4. 移除队列的第一个元素，作为初始节点，进行遍历，第一次默认取出index节点
  5. 横向查找节点index的第一个邻接节点nextIndex
  6. 若节点index的邻接节点nextIndex不存在，则转到步骤三

  7. 如果节点存在，则需要进行下面判断

    • 若节点nextIndex没有被访问，则访问节点并标记为已访问
    • 将节点nextIndex入队列；
    • 将nextIndex标记添加队列完成后，将nextIndex节点作为index节点，转到步骤五，继续处理
    • 一次遍历中，会持续往队列中添加元素，这也是第三步队列判空的意义；如果初始节点index存在三个横向的邻接节点，则第一次队列遍历完成后，队列中会移除index节点，并添加三个邻接节点，等第二次遍历时，队列中会有三个节点，并继续对这三个节点进行遍历
    • 尽量写明白点，看代码吧，目测看不懂…

3.3，代码实现

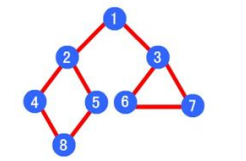
在这里插入图片描述

  • 广度优先运行结果：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8

    package com.self.datastructure.chart;

    import org.apache.commons.collections.CollectionUtils;

    import java.util.ArrayList;
    import java.util.Arrays;
    import java.util.LinkedList;
    import java.util.List;

    / 图基本入门 @author PJ_ZHANG @create 2020-04-20 16:16 /
    public class QuickStartChart { 

    1. public static void main(String[] args) { 
    2.     MyChart myChart = createChart(8);
    3.     System.out.println("深度优先遍历: ");
    4.     myChart.dfs();
    5. }
    7. /** * 创建图 * @param vertexNum 顶点数量 * @return */
    8. private static MyChart createChart(int vertexNum) { 
    9.     MyChart myChart = new MyChart(vertexNum);
    10.     for (int i = 1; i <= vertexNum; i++) { 
    11.         myChart.addVertex(String.valueOf(i));
    12.     }
    13.     myChart.addEdge(myChart.indexOf("1"), myChart.indexOf("2"), 1);
    14.     myChart.addEdge(myChart.indexOf("1"), myChart.indexOf("3"), 1);
    15.     myChart.addEdge(myChart.indexOf("2"), myChart.indexOf("4"), 1);
    16.     myChart.addEdge(myChart.indexOf("2"), myChart.indexOf("5"), 1);
    17.     myChart.addEdge(myChart.indexOf("3"), myChart.indexOf("6"), 1);
    18.     myChart.addEdge(myChart.indexOf("3"), myChart.indexOf("7"), 1);
    19.     myChart.addEdge(myChart.indexOf("4"), myChart.indexOf("8"), 1);
    20.     myChart.addEdge(myChart.indexOf("5"), myChart.indexOf("8"), 1);
    21.     return myChart;
    22. }
    24. /** * 自定义图类进行处理 */
    25. static class MyChart { 
    27.     /** * 顶点数量 */
    28.     private int vertexNum;
    30.     /** * 顶点列表 */
    31.     private List<String> lstVertex;
    33.     /** * 顶点路径 */
    34.     private int[][] vertexPathArray;
    36.     /** * 边数量 */
    37.     private int edgeNum;
    39.     /** * 是否已经被访问 */
    40.     private boolean[] isVisited;
    42.     MyChart(int vertexNum) { 
    43.         this.vertexNum = vertexNum;
    44.         lstVertex = new ArrayList<>(vertexNum);
    45.         vertexPathArray = new int[vertexNum][vertexNum];
    46.         isVisited = new boolean[vertexNum];
    47.     }
    49.     /** * 添加顶点, 此处不涉及扩容 * * @param vertex 添加的顶点 */
    50.     void addVertex(String vertex) { 
    51.         if (vertexNum == lstVertex.size()) { 
    52.             throw new ArrayIndexOutOfBoundsException("数组已满");
    53.         }
    54.         lstVertex.add(vertex);
    55.     }
    57.     /** * 添加多个顶点 * * @param vertexArr 顶点数组, 可变参数 */
    58.     void addAllVertex(String ... vertexArr) { 
    59.         if (vertexNum < lstVertex.size() + vertexArr.length) { 
    60.             throw new ArrayIndexOutOfBoundsException("数组已满");
    61.         }
    62.         lstVertex.addAll(Arrays.asList(vertexArr));
    63.     }
    65.     /** * 返回顶点所在的下标 * * @param vertex 目标顶点 * @return 返回下标 */
    66.     int indexOf(String vertex) { 
    67.         return lstVertex.indexOf(vertex);
    68.     }
    70.     /** * 添加边 * * @param xIndex 横坐标 * @param yIndex 纵坐标 * @param weight 边的权重 */
    71.     void addEdge(int xIndex, int yIndex, int weight) { 
    72.         if (xIndex >= vertexNum || yIndex >= vertexNum) { 
    73.             throw new IndexOutOfBoundsException("索引越界");
    74.         }
    75.         vertexPathArray[xIndex][yIndex] = weight;
    76.         vertexPathArray[yIndex][xIndex] = weight;
    77.         edgeNum++;
    78.     }
    80.     /** * 获取边数量 * * @return 返回边数量 */
    81.     int getEdgeNum() { 
    82.         return edgeNum;
    83.     }
    85.     /** * 展示图 */
    86.     void showChart() { 
    87.         for (int[] array : vertexPathArray) { 
    88.             System.out.println(Arrays.toString(array));
    89.         }
    90.     }
    92.     /** * 获取下一个邻接节点 * X, Y轴已知, 查找Y轴后面第一个存在权值的节点 * @param index * @param nextIndex * @return */
    93.     private int getNextNeighbor(int index, int nextIndex) { 
    94.         for (int i = nextIndex + 1; i < lstVertex.size(); i++) { 
    95.             if (vertexPathArray[index][i] > 0) { 
    96.                 return i;
    97.             }
    98.         }
    99.         return -1;
    100.     }
    102.     /** * 获取第一个邻接节点 * X轴已知, 获取Y轴上第一个存在权值的节点 * @param index * @return */
    103.     private int getFirstNeighbor(int index) { 
    104.         // 在该行坐标轴上进行遍历查找
    105.         // 如果对应坐标的权值大于0, 说明这两个点是有关联关系的
    106.         // 直接返回该点对应的下标索引
    107.         for (int i = 0; i < lstVertex.size(); i++) { 
    108.             if (vertexPathArray[index][i] > 0) { 
    109.                 return i;
    110.             }
    111.         }
    112.         // 如果没有找到, 直接返回-1
    113.         return -1;
    114.     }
    116.     /** * 广度优先遍历 */
    117.     public void bfs() { 
    118.         for (int i = 0; i < lstVertex.size(); i++) { 
    119.             if (!isVisited[i]) { 
    120.                 bfs(i);
    121.             }
    122.         }
    123.     }
    125.     private void bfs(int index) { 
    126.         LinkedList<Integer> lstSearch = new LinkedList<>();
    127.         // 添加节点到集合
    128.         lstSearch.add(index);
    129.         System.out.print(lstVertex.get(index) + " -> ");
    130.         // 标识节点为已经遍历
    131.         isVisited[index] = true;
    132.         // 队列不为空, 进行顺序处理
    133.         for (;CollectionUtils.isNotEmpty(lstSearch);) { 
    134.             // 获取队列第一个顶点
    135.             Integer currIndex = lstSearch.removeFirst();
    136.             // 获取顶点的邻接节点
    137.             int nextIndex = getFirstNeighbor(currIndex);
    138.             // 邻接节点存在
    139.             for (;-1 != nextIndex;) { 
    140.                 // 如果邻接节点没有被访问过
    141.                 if (!isVisited[nextIndex]) { 
    142.                     lstSearch.add(nextIndex);
    143.                     isVisited[nextIndex] = true;
    144.                     System.out.print(lstVertex.get(nextIndex) + " -> ");
    145.                 }
    146.                 // 获取下一个节点进行处理
    147.                 nextIndex = getNextNeighbor(currIndex, nextIndex);
    148.             }
    149.             // 当前顶点处理完成后, 注意循环开始数据已经被移除
    150.             // 如果集合不为空, 第二次开始时会继续移除下一个顶点, 并对该顶点进行处理
    151.         }
    152.     }
    154. }

    }

发表评论

表情：
评论列表 （有 0 条评论，143人围观）

还没有评论，来说两句吧...

相关阅读