题目描述

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

思路整理自windliang的题解——

思路1：暴力求解

遍历每个点，求以这个点为矩阵右下角的所有矩阵面积。如下图的两个例子，橙色是当前遍历到的点，虚线框圈出的矩阵是其中一个矩阵。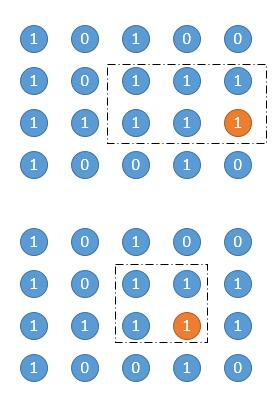
在这里插入图片描述
怎么找出这样的矩阵呢？如下图，如果我们知道了以这个点结尾的连续 1 的个数的话，问题就变得简单了。因此，我们遍历到一个点时，先求它的矩形“宽度”——以这个点结尾的连续 1 的个数，结果将保存在一个“宽度”矩阵中（下图右侧）：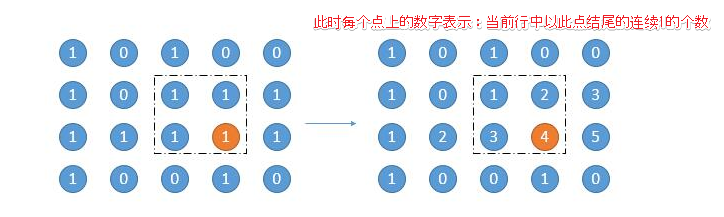
在这里插入图片描述
由此，在“宽度”矩阵上求该点的最大矩形面积的方法如下：

首先求出高度是 1 的矩形面积，也就是它自身的数，如图中橙色的 4，面积就是 4（宽度为4，高度为1）。
然后向上扩展一行，高度增加一，选出当前列最小的数字，作为矩阵的宽，求出面积，对应上图的矩形框（宽度为2，高度为2）。
然后继续向上扩展，重复步骤 2。

按照上边的方法，遍历所有的点，求出所有的矩阵就可以了。

时间复杂度：O（m²n）：遍历整个矩阵花费m*n，嵌套往上扩展花费m。
空间复杂度：O（mn）：额外的矩阵内存消耗。

代码

// 解法1
class Solution { 
    public int maximalRectangle(char[][] matrix) { 
        if (matrix.length == 0) { 
            return 0;
        }
        // width矩阵用于保存以当前数字结尾的连续 1 的个数
        int[][] width = new int[matrix.length][matrix[0].length];
        int maxArea = 0;
        // 遍历原阵的每一行
        for (int row = 0; row < matrix.length; row++) { 
            // 遍历每一列
            for (int col = 0; col < matrix[0].length; col++) { 
                // 更新width矩阵
                // 若当前位置为1
                if (matrix[row][col] == '1') { 
                    // 若为第1列，则width的此位置为1
                    // 否则在左边位置的基础上+1
                    // 直到出现0
                    if (col == 0) { 
                        width[row][col] = 1;
                    } else { 
                        width[row][col] = width[row][col - 1] + 1;
                    }
                } else { 
                    width[row][col] = 0;
                }
                // 记录当前列中最小的数
                int minWidth = width[row][col];
                // 向上扩展行
                for (int up_row = row; up_row >= 0; up_row--) { 
                    // 高度为矩形的长
                    int height = row - up_row + 1;
                    // 更新当前列最小的数，并用最小的数作为矩形的宽
                    minWidth = Math.min(minWidth, width[up_row][col]);
                    // 更新面积
                    maxArea = Math.max(maxArea, height * minWidth);
                }
            }
        }
        return maxArea;
    }
}

执行用时：28 ms, 在所有 Java 提交中击败了6.22%的用户
内存消耗：43.2 MB, 在所有 Java 提交中击败了32.81%的用户

思路2：拆分出子问题（单调栈）

优化思路中，首先要对leetcode-84 柱状图中最大的矩形这道题做一个回顾。
我们把矩阵中的1都视为柱状图，从上往下连续的1将组成一个柱。
从上往下遍历每一行，那么每一行都将出现不同的柱状图，用一个数组heights[] 来存当前层的柱体高度，如下图，橙色部分表示当前层的柱体，并且对应当前的heights[]。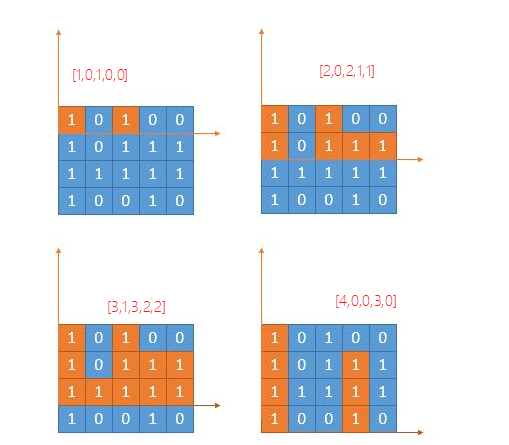
在这里插入图片描述
如此一来，求每一行对应的最大矩形面积，就相当于求当前层柱状图的最大矩形面积，这与leetcode-84 柱状图中最大的矩形其实就是同一个问题，我们可以直接使用该题的单调栈解法：

因此，解决本题的思路就是求出每一行对应的heights[] ，并调用84题的方法求heights[]对应的最大矩形，在整个过程中更新最大矩形面积即可。

时间复杂度：O（mn）：每一行单调栈解法花费O(n)，有m行。
空间复杂度：O（n）：有n列，数组空间开销。

代码

// 解法2
class Solution { 
    public int maximalRectangle(char[][] matrix) { 
        if (matrix.length == 0) { 
            return 0;
        }
        // 一维数组heights保存当前行的“柱高度”
        int[] heights = new int[matrix[0].length];
        int maxArea = 0;
        // 遍历每一行
        for (int row = 0; row < matrix.length; row++) { 
            // 遍历每一列，更新高度
            for (int col = 0; col < matrix[0].length; col++) { 
                if (matrix[row][col] == '1') { 
                    heights[col] += 1;
                } else { 
                    heights[col] = 0;
                }
            }
            // 调用上一题的解法，更新最大面积
            maxArea = Math.max(maxArea, largestRectangleArea(heights));
        }
        return maxArea;
    }
    // leetcode-84 柱状图中最大的矩形
    public int largestRectangleArea(int[] heights) { 
        // 这里为了代码简便，在柱体数组的头和尾加了两个高度为 0 的柱体。
        int[] tmp = new int[heights.length + 2];
        System.arraycopy(heights, 0, tmp, 1, heights.length); 
        // 栈中存的是坐标
        Stack<Integer> stack = new Stack<>();
        int area = 0;
        for (int i = 0; i < tmp.length; i++) { 
            // 对栈中柱体来说，栈中的下一个柱体就是其「左边第一个小于自身的柱体」；
            // 若当前柱体 i 的高度【小于】栈顶柱体的高度，说明 i 是栈顶柱体的「右边第一个小于栈顶柱体的柱体」。
            // 因此以【栈顶】柱体为高的矩形的左右宽度边界就确定了，可以计算面积
            while (!stack.isEmpty() && tmp[i] < tmp[stack.peek()]) { 
                // 计算栈顶柱的面积
                int curHeight = tmp[stack.pop()];
                area = Math.max(area, (i - stack.peek() - 1) * curHeight);   
            }
            stack.push(i);
        }
        return area;
    }
}