深度解析卷积神经网络中的卷积操作

亦凉 2023-03-04 03:29 115阅读 0赞

学习过信号处理的人知道，信号上的卷积操作是通过一个信号旋转后再在信号上进行移动逐渐得到重叠后的新信号。与图像上的卷积操作不同，图像上的卷积操作实际上是图像的感受野与卷积核进行加权和，终其原因是因为，数学上的卷积操作与图像上的卷积操作不同。

一、数学中的卷积

数学中的卷积操作分为两种，一种是连续函数进行卷积操作。另外一种是离散卷积操作。图像中由于是离散的点，以下将着重介绍离散卷积操作的详细步骤。

1、准备工作
矩阵的卷积准备一共是分为两个，一个是待处理矩阵X；一个是3x3的卷积核。

卷积核的矩阵如下；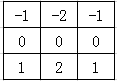
在这里插入图片描述
待处理矩阵X；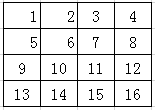
在这里插入图片描述
2、执行

第一步，将卷积核翻转180°，也就是成为了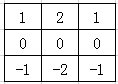
在这里插入图片描述
第二步，将卷积核h的中心对准x的第一个元素，然后对应元素相乘后相加，没有元素的地方补0。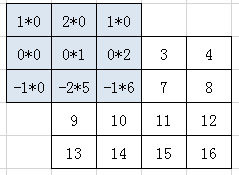
在这里插入图片描述
第三步，每个元素都像这样计算出来就可以得到一个输出矩阵，就是卷积结果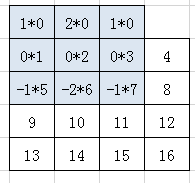
在这里插入图片描述
最后结果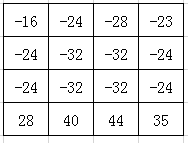
在这里插入图片描述

二、卷积神经网络中的卷积

其本质上是一种互相关函数计算或者说图像处理中的spatial filter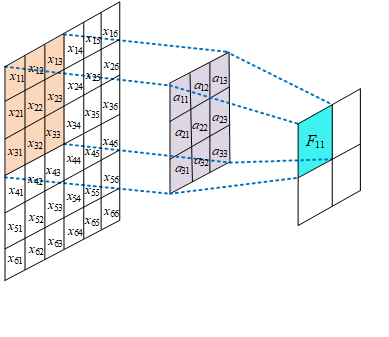
在这里插入图片描述
图像的卷积中是没有对卷积核进行反转的，而是直接通过图像对感受野上的值进行加权和，本质上图像处理是对图像上的特征进行特征提取，其反转的意义不大。

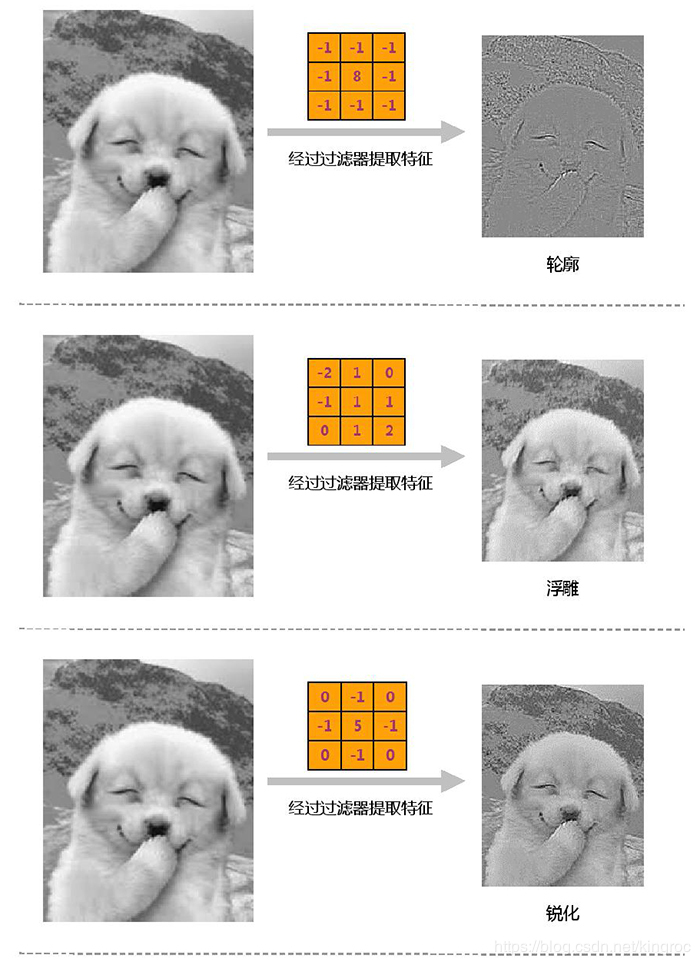
在这里插入图片描述

三、数学卷积和图像卷积的区别

最直观的就是：是否进行翻转，然后再进行对应元素的加权求和
其实本质上来说是两者的用途不同

  • 数学中的卷积，主要是为了诸如信号处理，求两个随机变量和的分部等而定义的运算，所以需要“翻转”是根据问题的需要而确定的。
  • 卷积神经网络中的“卷积”是为了提取图像的特征，其实只是为了借鉴”加权求和“的特点
  • 最后一点是，
    数学中的”卷积核“都是已知或者给定的，i卷积神经网络中的”卷积核“本身就是为了训练学习的参数，不是给定的，根据训练学习的，那么不反转和反转这项工作本身不存在什么本质的意义，因为无论是否进行反转，其对应的卷积核的参数都是未知数。

发表评论

表情：
评论列表 （有 0 条评论，115人围观）

还没有评论，来说两句吧...

相关阅读

    相关 卷积神经网络

    在介绍卷积神经网络之前我们先了解一下为什么不使用我们上一节介绍的神经网络（全连接层结构）来处理图像。使用全连接层结构处理图像时会出现以下问题： 输入图像需要将图像通过

    曾经终败给现在曾经终败给现在/ 0 赞/ 233 阅读

    相关 深度解析卷积神经网络中的卷积操作

    学习过信号处理的人知道，信号上的卷积操作是通过一个信号旋转后再在信号上进行移动逐渐得到重叠后的新信号。与图像上的卷积操作不同，图像上的卷积操作实际上是图像的感受野与卷积核进行加

    亦凉亦凉/ 0 赞/ 116 阅读

    相关 卷积神经网络

    概述 简单描述 首先介绍神经网络的参数。这些参数是由一些可学习的滤波器集合构成的，每个滤波器在空间上（宽度和高度）都比较小`个人觉得这个滤波器就是卷积核`，但是深度和

    浅浅的花香味﹌浅浅的花香味﹌/ 0 赞/ 553 阅读

    相关 卷积神经网络

    [卷积神经网络][Link 1]     在上篇中介绍的输入层与隐含层的连接称为全连接，如果输入数据是小块图像，比如8×8，那这种方法是可行的，但是如果输入图像是96×96，

    曾经终败给现在曾经终败给现在/ 0 赞/ 713 阅读