两棵树的最大公共子树_两棵镜树

两棵树的最大公共子树

Problem statement: Given a Two Binary Trees, write a function that returns true if one is mirror of other, else returns false.

问题陈述：给定两个二叉树，编写一个函数，如果一个是另一个的镜像，则返回true，否则返回false。

Solution

解

Check the below examples:

检查以下示例：

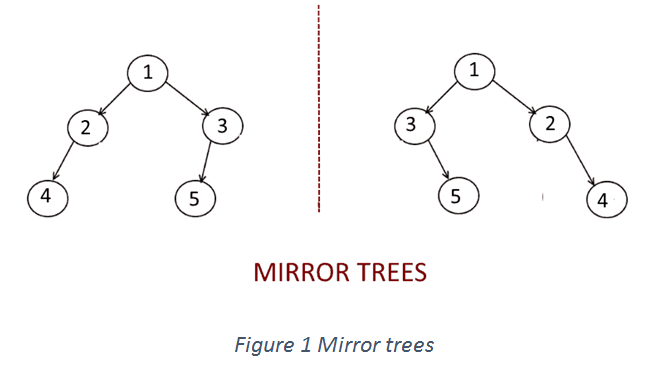
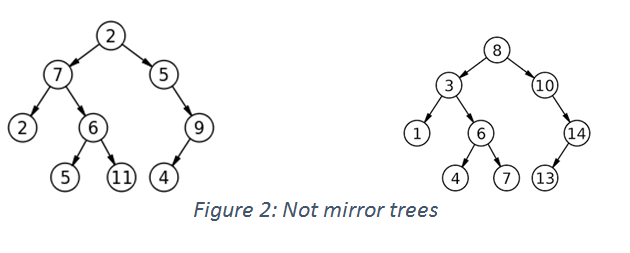
In figure 1, both the trees have the same root and one tree is mirror of other. Where as in In Figure 2, both trees are identical in shape and thus are not mirror trees at all and have different node values too.

在图1中，两棵树具有相同的根，一棵树是另一棵的镜像。 如图2所示，两棵树的形状相同，因此根本不是镜像树，并且节点值也不同。

So in general, two trees are said to be mirror trees of each other if they have the same root , left subtree (from root) of first tree is mirror of right subtree of second tree & right subtree of the first tree is mirror of left subtree of second tree.

因此，通常，如果两棵树具有相同的根，则称它们为彼此的镜像树，第一棵树的左子树(从根开始)是第二棵树的右子树的镜像，而第一棵树的右子树是左树的镜像第二棵树的子树 。

These are the three necessary & sufficient conditions to be checked for finding mirror trees.

这是查找镜像树需要检查的三个必要条件。

Algorithm:

算法：

1.  Define tree structure like:
    class tree{    // tree node is defined
        public:
        int data;
        tree *left;
        tree *right;
    };
    Or you can use struct instead of class
2.  Build both of the input tree.
3.  Recursive function AreMirror to check whether 
    both trees are mirror tree or not.
FUNCTION AreMirror (root of first tree, root of second tree)
    Root of first tree, root1
    Root of second tree root2
    FUNCTION AreMirror (root1, root2) 
        a.  Check base cases
            If root1==NULL&&root2==NULL
            Then it’s mirror tree, return true;
            If root1==NULL || root2==NULL
            Then it’s not a mirror tree, return false
            Because one root is NULL whether another is not. 
            (Both can’t be NULL here, since already checked before) 
            If root1->data != root2->data
            Then it’s not a mirror tree, return false.
            Because roots are different & thus can’t be mirror image of other
        b.  Recursively check for sub-trees
            return(AreMirror(root1->left, root2->right) 
            &&AreMirror(root1->right,root2->left));
END FUNCTION

Example & Explanation:

示例与说明：

Let’s check how the program works for the first example…

让我们检查第一个示例的程序工作方式…

N.B: Nodes are represented by their respective values.

注意：节点由它们各自的值表示。

Root1=1 and Root2=1
In the main it calls AreMirror (1, 1)
--------------------------------------------------
AreMirror (1, 1):
1->left =2 and 1->right=3 in case of tree1
1->left =3 and 1->right=2 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror ( 2, 2) && AreMirror ( 3, 3))
Call to AreMirror ( 2, 2) and AreMirror ( 3, 3)
--------------------------------------------------
AreMirror (2, 2):(call at AreMirror (1, 1))
2->left =4 and 2->right=NULL in case of tree1
2->left =NULL and 2->right=4 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (4, 4) && AreMirror (NULL, NULL))
Call to AreMirror (4, 4) and AreMirror (NULL, NULL))
--------------------------------------------------
AreMirror (3, 3): (call at AreMirror (1, 1))
3->left =5 and 3->right=NULL in case of tree1
3->left =NULL and 3->right=5 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (5, 5) && AreMirror (NULL, NULL))
Call to AreMirror (5, 5) && AreMirror (NULL, NULL)
--------------------------------------------------
AreMirror (4, 4): (call at AreMirror (2, 2))
4->left =NULL and 4->right=NULL in case of tree1
4->left =NULL and 4->right=NULL in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (NULL, NULL) && AreMirror (NULL, NULL))
Call to AreMirror (NULL, NULL) && AreMirror (NULL, NULL)
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (2, 2))
Base case matches and returns 1. 
--------------------------------------------------
AreMirror (5, 5): (call at AreMirror (3, 3))
5->left =NULL and 5->right=NULL in case of tree1
5->left =NULL and 5->right=NULL in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (NULL, NULL) && AreMirror (NULL, NULL))
Call to AreMirror (NULL, NULL) && AreMirror (NULL, NULL)
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (3, 3))
Base case matches and returns 1. 
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (4, 4))
Base case matches and returns 1. 
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (4, 4))
Base case matches and returns 1. 
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (5, 5))
Base case matches and returns 1. 
--------------------------------------------------
AreMirror (NULL, NULL): (call at AreMirror (5, 5))
Base case matches and returns 1. 
--------------------------------------------------
Thus at main,
AreMirror (1, 1) returns:
=   AreMirror ( 2, 2) && AreMirror ( 3, 3)
=   (AreMirror (4, 4) && AreMirror (NULL, NULL)) && 
    (AreMirror (5, 5) && AreMirror (NULL, NULL))
=   ((AreMirror (NULL, NULL) && AreMirror (NULL, NULL)) && 1) 
    &&((AreMirror (NULL, NULL) && AreMirror (NULL, NULL)) && 1)
=   ((1 && 1) &&1) && (1 && 1) &&1)
=   1
Thus they are mirror trees

用C ++实现检查两棵树是否是镜像？ (C++ implementation to check whether two trees are mirros?)

#include<bits/stdc++.h>
using namespace std;
class tree{
        // tree node is defined
    public:
    int data;
    tree *left;
    tree *right;
};
tree* newnode(int data)  // creating new node
{
    tree* node = (tree*)malloc(sizeof(tree)); 
    node->data = data; 
    node->left = NULL; 
    node->right = NULL; 
    return(node); 
} 
//function to check mirror tree
int areMirror(tree* a, tree* b)
{
   // base cases
   //if both root is NULL, then it's mirror tree
   if(a==NULL && b==NULL)
   return 1;
   //if one is NULL & other is not
   //then it's not mirror tree
   if(a==NULL || b==NULL)
   return 0;
   //if root data are different
   //not mirror tree
   if(a->data!=b->data)
   return 0;
   //check for subtrees recursively 
   return(areMirror(a->left,b->right) && areMirror(a->right,b->left));
}
int main(){
    //**same tree is builted as shown in example 1**
    cout<<"**same trees are built as shown in example 1**\n";
    tree *root1=newnode(1); 
    root1->left= newnode(2); 
    root1->right= newnode(3); 
    root1->left->left=newnode(4);
    root1->right->left=newnode(5);
    tree *root2=newnode(1); 
    root2->left= newnode(3); 
    root2->right= newnode(2); 
    root2->right->right=newnode(4);
    root2->left->right=newnode(5); 
    cout<<"printing whether mirror trees...\n"; 
    if(areMirror(root1,root2))//if returns 1
    cout<<"Both are mirror of each other\n";
    else
    cout<<"not mirror of each other\n";
    //**same tree is builted as shown in example 2**
    cout<<"**same trees are built as shown in example 2**\n";
    root1=newnode(2); 
    root1->left= newnode(7); 
    root1->right= newnode(5); 
    root1->right->right=newnode(9);
    root1->right->right->left=newnode(4);
    root1->left->left=newnode(2); 
    root1->left->right=newnode(6);
    root1->left->right->left=newnode(5);
    root1->left->right->right=newnode(11);
    root2=newnode(8); 
    root2->left= newnode(3); 
    root2->right= newnode(10); 
    root2->right->right=newnode(14);
    root2->right->right->left=newnode(13);
    root2->left->left=newnode(1); 
    root2->left->right=newnode(6);
    root2->left->right->left=newnode(4);
    root2->left->right->right=newnode(7);
    cout<<"printing whether mirror trees...\n"; 
    if(areMirror(root1,root2))//if returns 1
    cout<<"Both are mirror of each other\n";
    else
    cout<<"not mirror of each other\n";
    return 0;
 }

Output

输出量

**same trees are built as shown in example 1**
printing whether mirror trees...
Both are mirror of each other
**same trees are built as shown in example 2**
printing whether mirror trees...
not mirror of each other

翻译自: https://www.includehelp.com/icp/two-mirror-trees.aspx

两棵树的最大公共子树