695. Max Area of Island (Medium)——岛屿的最大面积

前言：

本题目为深度优先遍历（DFS）算法的一道典型例题。

题目：

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个岛屿是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

解题算法：

DFS:

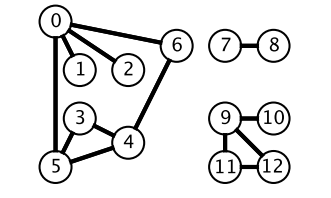
format_png

广度优先搜索一层一层遍历，每一层得到的所有新节点，要用队列存储起来以备下一层遍历的时候再遍历。

而深度优先搜索在得到一个新节点时立即对新节点进行遍历：从节点 0 出发开始遍历，得到到新节点 6 时，立马对新节点 6 进行遍历，得到新节点 4；如此反复以这种方式遍历新节点，直到没有新节点了，此时返回。返回到根节点 0 的情况是，继续对根节点 0 进行遍历，得到新节点 2，然后继续以上步骤。

从一个节点出发，使用 DFS 对一个图进行遍历时，能够遍历到的节点都是从初始节点可达的，DFS 常用来求解这种 可达性问题。

在程序实现 DFS 时需要考虑以下问题：

栈：用栈来保存当前节点信息，当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
标记：和 BFS 一样同样需要对已经遍历过的节点进行标记。

思路：

最外层用两个for循环对grid[][]数组的每个元素进行遍历，如果元素值为0，则continue跳过。如果值为1则说明可达，就对其进行深度优先遍历，找到以该元素为起点的岛屿的最大面积，并与之前的maxArea作比较，取最大值。当所有元素都遍历完之后，也就得到了最终的最大值。

对方法findMax的描述是：该方法接收一个坐标position，既然这个坐标传了过来，说明这个点是符合要求的，先令maxArea=1。然后对这个点进行四个方向的移动，得到移动后不符合要求的点就continue跳过，如果符合要求就对改点再进行深度优先遍历，并让maxArea加上改点进行深度优先遍历的到的最大面积。

这里虽然用的是递归，没有用到上文所说的“栈”，但二者起的作用却是一样的，递归的调用与“栈”的思想极为相似，感兴趣的童鞋也可以试试用Stack结合循环来解题~

代码：

public class MaxAreaOfIsland {
    private int m, n;
    int[][] directions = {
   {1, 0},{-1, 0},{0, 1},{0, -1}};
    public int maxAreaOfIsland(int[][] grid) {
        if (grid == null || grid.length==0) return 0;
        int maxArea = 0;
        m = grid.length;
        n = grid[0].length;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 0) continue;
                maxArea = Math.max(maxArea, findMax(grid, new Pair(i,j)));
            }
        }
        return maxArea;
    }
    public int findMax(int[][] grid, Pair<Integer, Integer> position) {
        int maxArea = 1;
        int r = position.getKey(), c = position.getValue();
        grid[r][c] = 0;
        for (int[] direction : directions) {
            int cr = r + direction[0];
            int cc = c + direction[1];
            if (cr < 0 || cr >= m || cc < 0 || cc >= n || grid[cr][cc]==0) continue;
            maxArea += findMax(grid, new Pair(cr, cc));
        }
        return maxArea;
    }
}