分段线性插值 PWL-蒲公英云

分段线性插值 PWL

亦凉 2023-06-04 08:56 79阅读 0赞

分段线性插值故名思议就是说把给定样本点的区间分成多个不同区间，记为[xi,xi+1]，在每个区间上的一次线性方程为：

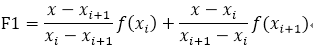
Center

关于其证明：

Center 1

分段线性插值在速度和误差取得了很好的平衡，插值函数具有连续性，但是由于在已知点的斜率是不变的，所以插值结果不光滑。

第一次用matlab写代码，有点手生。

liner.m文件：

function yy = liner(x,y,xx)
%x是已知数据点的x值
%y是已知数据点的y值
%是待插入点的横坐标值
%假设输入的样本点的x值是依次增大的
syms t;
if(length(x)==length(y))
n=length(x);
else
disp(‘x和y维数不相等！’);
return;
end

for i=1:n-1
% disp([‘区间为’,num2str(x(i)),’-‘,num2str(x(i+1))]);
yy(i)=((t-x(i+1))/(x(i)-x(i+1)))*y(i)+((t-x(i))/(x(i+1)-x(i)))*y(i+1);
end

if(nargin==3)
nn=length(xx);
for i=1:nn
for j=1:n-1
if(xx(i)>x(j)&xx(i)<=x(j+1))
yynum(i)=subs(yy(j),’t’,xx(i)); %计算插值点的函数值.subs是替换函数，把x0用t替换
end
end
end
yy=yynum;
else
yy=collect(yy); %将插值多项式展开
yy=vpa(yy,6); %将插值多项式的系数化成6位精度的小数
end
end

linerInsert.m文件：

x=0:2*pi;
y=sin(x);
xx=0:0.2:6;
yy=liner(x,y,xx);
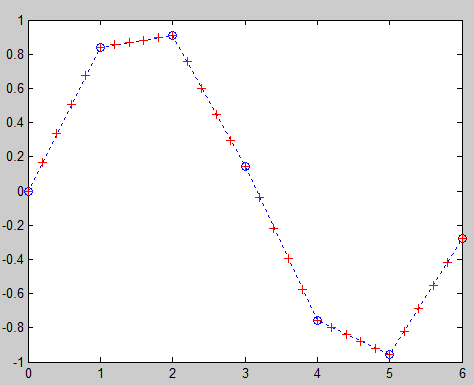
plot(x,y,’o:’,xx,yy,’+r’)

可以看到插值结果：

Center 2