机器学习算法之KMeans聚类

以你之姓@ 2023-06-06 10:52 2阅读 0赞

# 算法原理 #

聚类指的是把集合，分组成多个类，每个类中的对象都是彼此相似的。K-means是聚类中最常用的方法之一，它是基于点与点距离的相似度来计算最佳类别归属。

在使用该方法前，要注意（1）对数据异常值的处理；（2）对数据标准化处理（x-min(x))/(max(x)-min(x)）；（3）每一个类别的数量要大体均等；（4）不同类别间的特质值应该差异较大。

# 算法流程 #

（1）选择k个初始聚类中心

（2）计算每个对象与这k个中心各自的距离，按照最小距离原则分配到最邻近聚类

（3）使用每个聚类中的样本均值作为新的聚类中心

（4）重复步骤（2）和（3）直到聚类中心不再变化

（5）结束，得到k个聚类

# 代码实现 #

#coding=utf-8
    from collections import Counter
    from copy import deepcopy
    from time import time
    from random import randint, seed, random
    
    # 统计程序运行时间函数
    # fn代表运行的函数
    def run_time(fn):
        def fun():
            start = time()
            fn()
            ret = time() - start
            if ret < 1e-6:
                unit = "ns"
                ret *= 1e9
            elif ret < 1e-3:
                unit = "us"
                ret *= 1e6
            elif ret < 1:
                unit = "ms"
                ret *= 1e3
            else:
                unit = "s"
            print("Total run time is %.1f %s\n" % (ret, unit))
        return fun()
    
    def load_data():
        f = open("boston/breast_cancer.csv")
        X = []
        y = []
        for line in f:
            line = line[:-1].split(',')
            xi = [float(s) for s in line[:-1]]
            yi = line[-1]
            if '.' in yi:
                yi = float(yi)
            else:
                yi = int(yi)
            X.append(xi)
            y.append(yi)
        f.close()
        return X, y
    
    # 将数据归一化到[0, 1]范围
    def min_max_scale(X):
        m = len(X[0])
        x_max = [-float('inf') for _ in range(m)]
        x_min = [float('inf') for _ in range(m)]
        for row in X:
            x_max = [max(a, b) for a, b in zip(x_max, row)]
            x_min = [min(a, b) for a, b in zip(x_min, row)]
    
        ret = []
        for row in X:
            tmp = [(x - b) / (a - b) for a, b, x in zip(x_max, x_min, row)]
            ret.append(tmp)
        return ret
    
    def get_euclidean_distance(arr1, arr2):
        return sum((x1 - x2) ** 2 for x1, x2 in zip(arr1, arr2)) ** 0.5
    
    def get_cosine_distance(arr1, arr2):
        numerator = sum(x1 * x2 for x1, x2 in zip(arr1, arr2))
        denominator = (sum(x1 ** 2 for x1 in arr1) *
                       sum(x2 ** 2 for x2 in arr2)) ** 0.5
        return numerator / denominator
    
    
    class KMeans(object):
        # k 簇的个数
        # n_features 特征的个数
        # clister_centers 聚类中心
        # distance_fn 距离计算函数
        # cluster_samples_cnt 每个簇里面的样本数
        def __init__(self):
            self.k = None
            self.n_features = None
            self.cluster_centers = None
            self.distance_fn = None
            self.cluster_samples_cnt = None
    
        # 二分，查找有序列表里面大于目标值的第一个值
        def bin_search(self, target, nums):
            low = 0
            high = len(nums) - 1
            assert nums[low] <= target < nums[high], "Cannot find target!"
            while 1:
                mid = (low + high) // 2
                if mid == 0 or target >= nums[mid]:
                    low = mid + 1
                elif target < nums[mid - 1]:
                    high = mid - 1
                else:
                    break
            return mid
    
        # 比较两个向量是否为同一向量
        def cmp_arr(self, arr1, arr2, eps=1e-8):
            return len(arr1) == len(arr2) and \
                   all(abs(a- b) < eps for a, b in zip(arr1, arr2))
    
        # 初始化聚类中心
        def init_cluster_centers(self, X, k, n_features, distance_fn):
            n = len(X)
            centers = [X[randint(0, n-1)]]
            for _ in range(k-1):
                center_pre = centers[-1]
                idxs_dists = ([i, distance_fn(Xi, center_pre)] for i, Xi in enumerate(X))
                # 对距离进行排序
                idxs_dists = sorted(idxs_dists, key=lambda x: x[1])
                dists = [x[1] for x in idxs_dists]
                tot = sum(dists)
                for i in range(1, n):
                    dists[i] /= tot
                for i in range(1, n):
                    dists[i] += dists[i-1]
                # 随机选择一个聚类中心
                while 1:
                    num = random()
                    # 查找>=num的距离
                    dist_idx = self.bin_search(num, dists)
                    row_idx = idxs_dists[dist_idx][0]
                    center_cur = X[row_idx]
                    if not any(self.cmp_arr(center_cur, center) for center in centers):
                        break
                centers.append(center_cur)
            return centers
    
    
        # 寻找距离Xi最近的聚类中心
        def get_nearest_center(self, Xi, centers, distance_fn):
            return min(((i, distance_fn(Xi, center)) for
                        i, center in enumerate(centers)), key=lambda x: x[1])[0]
    
        # 寻找X最近的聚类中心
        def get_nearest_centers(self, X, distance_fn, centers):
            return [self.get_nearest_center(Xi, centers, distance_fn) for Xi in X]
    
        # 获取空的簇
        def get_empty_cluster_idxs(self, cluster_samples_cnt, k):
            clusters = ((i, cluster_samples_cnt[i]) for i in range(k))
            empty_clusters = filter(lambda x: x[1] == 0, clusters)
            return [empty_clusters[0] for empty_cluster in empty_clusters]
        # 在X中找到到所有非空簇中心的最远样本
        def get_furthest_row(self, X, distance_fn, centers, empty_cluster_idxs):
            def f(Xi, centers):
                return sum(distance_fn(Xi, centers) for center in centers)
    
            non_empty_centers = map(lambda x: x[1], filter(
                lambda x: x[0] not in empty_cluster_idxs, enumerate(centers)))
            return max(map(lambda x: [x, f(x, non_empty_centers)], X), key=lambda x: x[1])[0]
    
        # 处理空的簇
        def process_empty_clusters(self, X, distance_fn, n_features, centers, empty_cluster_idxs):
            for i in empty_cluster_idxs:
                center_cur = self.get_furthest_row(X, distance_fn, centers, empty_cluster_idxs)
                while any(self._cmp_arr(center_cur, center) for center in centers):
                    center_cur = self.get_furthest_row(X, distance_fn, centers,
                                                        empty_cluster_idxs)
                centers[i] = center_cur
            return centers
    
        # 重新获取聚类中心
        def get_cluster_centers(self, X, k, n_features, y, cluster_samples_cnt):
            ret = [[0 for _ in range(n_features)] for _ in range(k)]
            for Xi, cetner_num in zip(X, y):
                for j in range(n_features):
                    ret[cetner_num][j] += Xi[j] / cluster_samples_cnt[cetner_num]
            return ret
    
        # 训练
        def fit(self, X, k, fn=None, n_iter=100):
            n_features = len(X[0])
            if fn is None:
                distance_fn = get_euclidean_distance
            else:
                error_msg = "Parameter distance_fn must be eu or cos!"
                assert fn in ("eu", "cos"), error_msg
                if fn == "eu":
                    distance_fn = get_euclidean_distance
                if fn == "cos":
                    distance_fn = get_cosine_distance
    
            centers = self.init_cluster_centers(X, k, n_features, distance_fn)
            for i in range(n_iter):
                while 1:
                    # 寻找X的最近聚类中心
                    y = self.get_nearest_centers(X, distance_fn, centers)
                    # 统计每个簇的样本个数
                    cluster_samples_cnt = Counter(y)
                    # 获取空的簇
                    empty_cluster_idxs = self.get_empty_cluster_idxs(cluster_samples_cnt, k)
                    # 如果有空的簇
                    if empty_cluster_idxs:
                        centers = self.process_empty_clusters(centers, empty_cluster_idxs, n_features)
                    else:
                        break
                centers_new = self.get_cluster_centers(X, k, n_features, y, cluster_samples_cnt)
                centers = deepcopy(centers_new)
                print("Iteration: %d" % i)
            self.k = k
            self.n_features = n_features
            self.distance_fn = distance_fn
            self.cluster_centers = centers
            self.cluster_samples_cnt = cluster_samples_cnt
    
        def _predict(self, Xi):
            return self.get_nearest_center(Xi, self.cluster_centers, self.distance_fn)
    
        def predict(self, X):
            return [self._predict(Xi) for Xi in X]
    
    
    @run_time
    def main():
        print("Tesing the performance of Kmeans...")
        # Load data
        X, y = load_data()
        X = min_max_scale(X)
        # Train model
        est = KMeans()
        k = 2
        est.fit(X, k)
        print()
        # Model performance
        prob_pos = sum(y) / len(y)
        print("Positive probability of X is:%.1f%%.\n" % (prob_pos * 100))
        y_hat = est.predict(X)
        cluster_pos_tot_cnt = {i: [0, 0] for i in range(k)}
        for yi_hat, yi in zip(y_hat, y):
            cluster_pos_tot_cnt[yi_hat][0] += yi
            cluster_pos_tot_cnt[yi_hat][1] += 1
        cluster_prob_pos = {k: v[0] / v[1] for k, v in cluster_pos_tot_cnt.items()}
        for i in range(k):
            tot_cnt = cluster_pos_tot_cnt[i][1]
            prob_pos = cluster_prob_pos[i]
            print("Count of elements in cluster %d is:%d." %
                  (i, tot_cnt))
            print("Positive probability of cluster %d is:%.1f%%.\n" % (i, prob_pos * 100))

# 对肺癌数据集聚类100轮结果展示 #

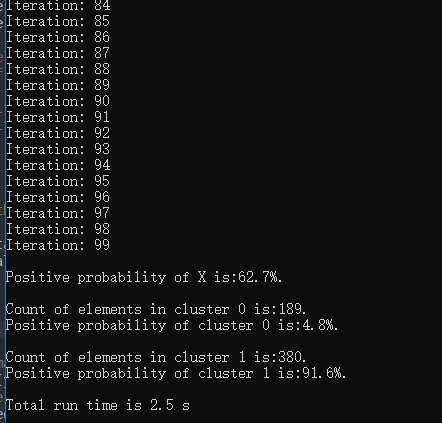
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2p1c3Rfc29ydA_size_16_color_FFFFFF_t_70]  
可以看到经过100次聚类后，正负样本被大量聚集在了一起，证明了聚类算法的有效性。

# github源码 #

https://github.com/BBuf/machine-learning

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2p1c3Rfc29ydA_size_16_color_FFFFFF_t_70]: /images/20230601/df5c2449148545389d875565724f987d.png