LeetCode题解——分治算法-蒲公英云

LeetCode题解——分治算法

文章目录

- 1. 为运算表达式设计优先级
- - 分治算法
- 1. 不同的二叉搜索树 II

241. 为运算表达式设计优先级

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。

示例 1:
输入: "2-1-1"
输出: [0, 2]
解释: 
((2-1)-1) = 0 
(2-(1-1)) = 2
示例 2:
输入: "2*3-4*5"
输出: [-34, -14, -10, -10, 10]
解释: 
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

分治算法

按运算符分成左右两部分，分别计算后，利用分隔符，合并。
举个例子：23-45
第一次按分割，左边2，右边3-45
左边没有运算符，则直接等于2;右边继续分割，左边3，右边45，再继续分割右边，运算45=20,将3-20=-17返回，再计算2*(-17)=34压入vector;
接下来从-号开始分割，依次下去，就求出所有可能。

vector<int> partition(string input)
{
    vector<int> ans;
    if(input.find('+')==string::npos && input.find('-')==string::npos && input.find('*')==string::npos) //input 不包含+ - *
    {
        ans.push_back(stoi(input));
        return ans;
    }
    for(int i = 0; i < input.length(); ++i)
        if(input[i] == '+' || input[i] == '-' || input[i] == '*')
            for(auto left : partition(input.substr(0, i)))
                for(auto right : partition(input.substr(i+1)))
                {
                    if(input.at(i) == '+')
                        ans.push_back(left + right);
                    else if(input.at(i) == '-')
                        ans.push_back(left - right);
                    else if(input.at(i) == '*')
                        ans.push_back(left * right);
                }
    return ans;
}
class Solution {
public:
    vector<int> diffWaysToCompute(string input) {
        vector<int> v2 = partition(input);
        sort(v2.begin(), v2.end());
        return v2;
    }
};

95. 不同的二叉搜索树 II

给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树。

示例:

输入: 3
输出:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：
   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

首先来计数需要构建的二叉树数量。可能的二叉搜素数数量是一个卡特兰数。
n个节点可以组成f(n)个二叉搜索树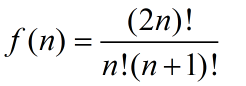
format_png
我们从序列 1 …n 中取出数字 i，作为当前树的树根。于是，剩余 i - 1 个元素可用于左子树，n - i 个元素用于右子树。
如前文所述，这样会产生 G(i - 1) 种左子树和 G(n - i) 种右子树，其中 G 是卡特兰数。

现在，我们对序列 1 … i - 1 重复上述过程，以构建所有的左子树；然后对 i + 1 … n 重复，以构建所有的右子树。

这样，我们就有了树根 i 和可能的左子树、右子树的列表。

最后一步，对两个列表循环，将左子树和右子树连接在根上。

class Solution {
public:
    vector<TreeNode*> all_trees(int start, int end)
    {
        vector<TreeNode*> ans;
        if(start > end)
        {
            ans.push_back(nullptr);
            return ans;
        }
        for(int i = start; i <= end; ++i)
        {
            vector<TreeNode*> left = all_trees(start, i-1);
            vector<TreeNode*> right = all_trees(i+1, end);
            for(auto l : left)
                for(auto r : right)
                {
                    TreeNode* root = new TreeNode(i);
                    root->left = l;
                    root->right = r;
                    ans.push_back(root);
                }
        }
        return ans;
    }
    vector<TreeNode*> generateTrees(int n) {
        vector<TreeNode*> ans;
        if(n == 0)
            return ans;
        else
            ans = all_trees(1, n);
        return ans;
    }
};