矩阵连乘
给定n个矩阵:A1,A2,…,An,其中Ai与Ai+1是可乘的,i=1,2…,n-1。确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模,输出结果为计算矩阵连乘积的计算次序和最少数乘次数。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用 2 个矩阵相乘的标准算法计算出矩阵连乘积。完全加括号的矩阵连乘积可递归地定义为:
( 1 )单个矩阵是完全加括号的;
( 2 )矩阵连乘积 A 是完全加括号的,则 A 可表示为 2 个完全加括号的矩阵连乘积 B 和 C 的乘积并加括号,即 A= ( BC )。
分析:
矩阵连乘的条件:第一个矩阵的列等于第二个矩阵的行,此时两个矩阵是可乘的;
多个矩阵连乘的结果矩阵,其行等于第一个矩阵的行和其列等于最后一个矩阵的列。
3.两个矩阵相乘的计算量:
例如:A(4*2),B(2*5) 可知总执行次数为:4×2×5=40
所以矩阵A m*n和B n*k的乘法运算次数为:m*n*k;
- 子问题的拆分,在(AiAi+1……Aj)中,先选择一个矩阵Ak,这样的话就将一个大矩阵拆分为两个小矩阵;假设在第k位置上找到最优解,则问题变成了两个子问题:(AiAi+1……Ak),(Ak+1……Aj);用m[i][j]表示矩阵连乘的最优值,那么两个子问题对应的最优值变成m[i][k],m[k+1][j];
矩阵连乘最优值递归式:
include
define N 100// 定义最大连乘的矩阵个数为 100 个
void matrixChain (int p[],int m[N+1][N+1],int s[N+1][N+1])
/ 用 m[i][j] 二维数组来存储 Ai……Aj 的最小数乘次数,用 s[i][j] 来存储使 Ai……Aj 获得最小数乘次数对应的断开位置 k ,需要注意的是此处的 N+1 非常关键,虽然只用到的行列下标只从 1 到 N 但是下标 0 对应的元素默认也属于该数组,所以数组的长度就应该为 N+1/
{
int n=N;// 定义 m,s 数组的都是 nn 的,不用行列下标为 0 的元素,但包括在该数组中
for (int i=1;i<=n;i++)
m[i][i]=0; / 将矩阵 m 的对角线位置上元素全部置 0 ,此时应是 r=1 的情况,表示先计算第一层对角线上个元素的值 /
for (int r=2;r<=n;r++)//r 表示斜对角线的层数,从 2 取到 n
{
for (int i=1;i<=n-r+1;i++)//i 表示计算第 r 层斜对角线上第 i 行元素的值
{int j=i+r-1;//j 表示当斜对角线层数为 r ,行下标为 i 时的列下标m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];// 计算当断开位置为 i 时对应的数乘次数s[i][j]=i;// 断开位置为 ifor (int k=i+1;k<j;k++){int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];/* 计算当断开位置 k 为从 i 到 j (不包括 i 和 j )的所有取值对应的 (Ai*......*Ak)*(Ak+1*.......Aj) 的数乘次数 */if (t<m[i][j]){m[i][j]=t;// 将 Ai*......Aj 的最小数乘次数存入 m[i][j]s[i][j]=k;// 将对应的断开位置 k 存入 s[i][j]}}
}
}
}
void traceback (int i,int j,int s[][N+1])// 用递归来实现输出得到最小数乘次数的表达式
{
if (i==j)
{
printf (“A%d”,i);
}
else
{
printf (“(“);
traceback (i,s[i][j],s);
traceback(s[i][j]+1,j,s);
printf (“)”);
}
}
int main ()
{
int n;// 用来存储矩阵的个数
int Q[2N];/ 用 Q 数组来存储最原始的输入(各矩阵的行和列),主要目的是为了检验这 N 个矩阵是否满足连乘的条件 /
int p[N+1],flag=1;/ 用 p[i-1],p[i] 数组来存储 A 的阶数, flag 用来判断这 N 个矩阵是否满足连乘 /
int m[N+1][N+1];// 用 m[i][j] 二维数组来存储 Ai……Aj 的最小数乘次数
int s[N+1][N+1];// 用 s[i][j] 来存储使 Ai……Aj 获得最小数乘次数对应的断开位置 k
printf (“ 请输入矩阵的个数(小于 100 ) :”);
scanf (“%d”,&n);
for (int i=0;i<=2*n-1;i++)// 各矩阵的阶数的输入先存入数组 Q 中接受检验
{
if (i%2==0)
{printf ("\n");printf (" 请输入A%d的 行 :",(i/2)+1);
}
else
{printf (" 列:");
}
scanf (“%d”,&Q[i]);
}
for (int i=1;i<=2*n-2;i++)// 矩阵连乘条件的检验
{
if (i%2!=0&&Q[i]!=Q[i+1])
{flag=0;break;
}
}
for (int j=1;j<=n-1;j++)
{p[j]=Q[2*j];
}
if (flag!=0)
{
p[0]=Q[0];
p[n]=Q[2*n-1];
matrixChain (p,m,s);
printf (“ 式子如下 :\n”);
traceback(1,n,s);
printf (“\n”);
printf (“ 最小数乘次数为 %d\n”,m[1][n]);
}
else
{
printf (“ 这 %d 个矩阵不能连乘 !\n”,n);
}
}
- 实验结果与分析
(1)实验结果
1.输入正确结果的情况
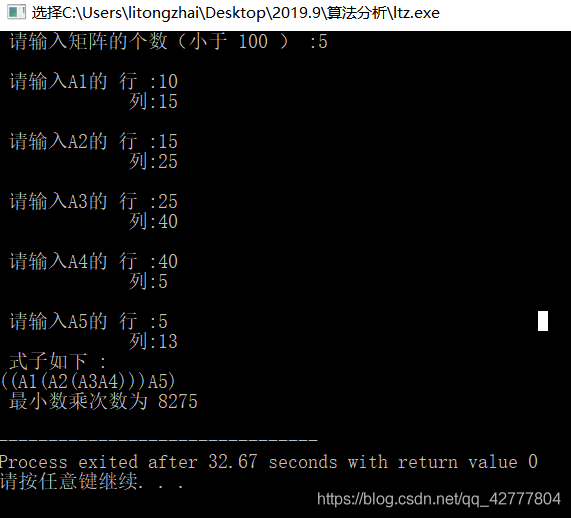
- 输入有误的情况:
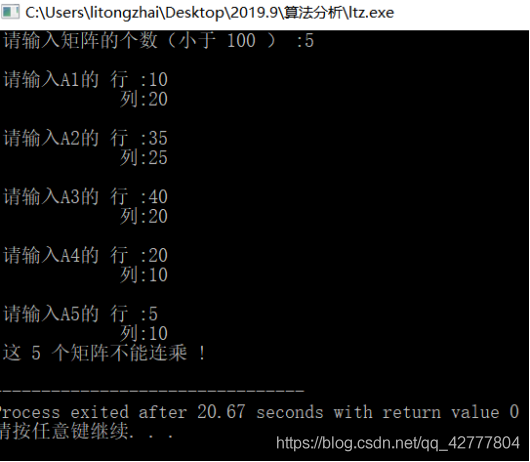
(2)分析与收获
经过这个对这个程序的了解和深入研究,渐渐理解了动态规划的基本思想。































还没有评论,来说两句吧...