使用余弦相似度计算文本相似度
1. 使用simhash计算文本相似度
2. 使用余弦相似度计算文本相似度
3. 使用编辑距离计算文本相似度
4. jaccard系数计算文本相似度
2.向量余弦计算文本相似度
2.1 原理
余弦相似性:两个向量的夹角越接近于0,其余弦值越接近于1,表面两个向量越相似。
向量夹角余弦计算:
c o s α = x 1 ⋅ x 2 + y 1 ⋅ y 2 x 1 2 + y 1 2 × x 2 2 + y 2 2 cos α = \frac{x_1·x_2 + y_1·y_2}{\sqrt{x_1^2+y_1^2}×\sqrt{x_2^2+y_2^2}} cosα=x12+y12×x22+y22x1⋅x2+y1⋅y2
文本相似度计算大致流程:
- 分词
- 合并
- 计算特征值
- 向量化
- 计算向量夹角余弦值
对于两段文本A和B,对其进行分词,得到两个词列表:
A = [ t 1 , t 2 , ⋯ , t i ] A=[t_1, t_2, \cdots, t_i] A=[t1,t2,⋯,ti]
B = [ t 1 , t 2 , ⋯ , t j ] B=[t_1, t_2, \cdots, t_j] B=[t1,t2,⋯,tj]
对两个词列表进行合并去重,得到输入样本中的所有词:
T ( A , B ) = T ( A ) + T ( B ) = [ t 1 , t 2 , ⋯ , t k ] T(A,B)=T(A)+T(B)=[t_1,t_2, \cdots , t_k] T(A,B)=T(A)+T(B)=[t1,t2,⋯,tk]
计算特征值:
选取词频作为特征值。
F ( A ) = [ f A 1 , f A 2 , ⋯ , f A k ] F(A)=[f_{A_1},f_{A_2},\cdots,f_{A_k}] F(A)=[fA1,fA2,⋯,fAk]
F ( B ) = [ f B 1 , f B 1 , ⋯ , f B k ] F(B)=[f_{B_1},f_{B_1},\cdots,f_{B_k}] F(B)=[fB1,fB1,⋯,fBk]
向量化
A ⃗ = ( f A 1 , f A 2 , ⋯ , f A k ) \vec{A}=(f_{A_1},f_{A_2},\cdots,f_{A_k}) A=(fA1,fA2,⋯,fAk)
B ⃗ = ( f B 1 , f B 2 , ⋯ , f B k ) \vec{B}=(f_{B_1},f_{B_2},\cdots,f_{B_k}) B=(fB1,fB2,⋯,fBk)
计算余弦值:
c o s α = ∑ i = 1 k f A i ⋅ f B i ∑ i = 1 k ( f A i ) 2 ⋅ ∑ i = 1 k ( f B i ) 2 cos α = \frac{\sum_{i=1}^{k}f_{A_i}·f_{B_i}}{\sqrt{\sum_{i=1}^{k}(f_{A_i})^2}·\sqrt{\sum_{i=1}^{k}(f_{B_i})^2}} cosα=∑i=1k(fAi)2⋅∑i=1k(fBi)2∑i=1kfAi⋅fBi
2.2举例
样本1( A ):今天天气真好,适合去逛街,也适合晒太阳。
样本2( B ):今天天气不错,适合去玩,也适合去晒太阳。
样本3( C ):小明不喜欢和小红玩,因为小明不喜欢太阳。
分词:
A=[今天, 天气, 真好, 适合, 去, 逛街, 也, 适合, 晒太阳]B=[今天, 天气, 不错, 适合, 去, 玩, 也, 适合, 去, 晒太阳]C=[小明, 不, 喜欢, 和, 小, 红, 玩, 因为, 小明, 不, 喜欢, 太阳]
合并并去重:
[今天, 天气, 真好, 适合, 去, 逛街, 也, 晒太阳, 小明, 不, 喜欢, 和, 小, 红, 玩, 因为, 太阳, 不错]
特征值(词频)计算:
F(A) = [今天:1, 天气:1, 真好:1, 适合:2, 去:1, 逛街:1, 也:1, 晒太阳:1, 小明:0, 不:0, 喜欢:0, 和:0, 小:0, 红:0, 玩:0, 因为:0, 太阳:0, 不错:0]F(B) = [今天:1, 天气:1, 真好:0, 适合:2, 去:2, 逛街:0, 也:1, 晒太阳:1, 小明:0, 不:0, 喜欢:0, 和:0, 小:0, 红:0, 玩:1, 因为:0, 太阳:0, 不错:1]F(C) = [今天:1, 天气:1, 真好:0, 适合:2, 去:2, 逛街:0, 也:1, 晒太阳:1, 小明:2, 不:2, 喜欢:2, 和:1, 小:1, 红:1, 玩:2, 因为:1, 太阳:1, 不错:1]
向量化:
A ⃗ = ( 1 , 1 , 1 , 2 , 1 , 1 , 1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ) \vec{A}=(1, 1, 1, 2, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) A=(1,1,1,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0)
B ⃗ = ( 1 , 1 , 0 , 2 , 2 , 0 , 1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 0 , 1 ) \vec{B}=(1, 1, 0, 2, 2, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1) B=(1,1,0,2,2,0,1,1,0,0,0,0,0,0,1,0,0,1)
C ⃗ = ( 1 , 1 , 0 , 2 , 2 , 0 , 1 , 1 , 2 , 2 , 2 , 1 , 1 , 1 , 2 , 1 , 1 , 1 ) \vec{C}=(1, 1, 0, 2, 2, 0, 1, 1, 2, 2, 2, 1, 1, 1, 2, 1, 1, 1) C=(1,1,0,2,2,0,1,1,2,2,2,1,1,1,2,1,1,1)
计算余弦:
c o s A ⃗ B ⃗ = 0.8058229640253802 cos \vec{A}\vec{B}=0.8058229640253802 cosAB=0.8058229640253802
c o s A ⃗ C ⃗ = 0.0 cos \vec{A}\vec{C}=0.0 cosAC=0.0
c o s B ⃗ C ⃗ = 0.06299407883487121 cos \vec{B}\vec{C}=0.06299407883487121 cosBC=0.06299407883487121
A ⃗ B ⃗ \vec{A}\vec{B} AB的夹角的余弦更趋近于1,所以相似度更高。
2.3 总结
余弦相似度对于短文本的相似度计算还是比较准确的,但是对于大文本计算时,速度不如simhash快。
以下测试分别通过simhash和余弦相似度计算相似度的时间:
| 字符数 | simhash耗时/ms | 余弦相似度耗时/ms |
|---|---|---|
| 20 | 1.7 | 0.4 |
| 200 | 4.2 | 1.8 |
| 2000 | 20.0 | 10.7 |
| 20000 | 24.1 | 34.0 |
| 200000 | 176.7 | 668.5 |
另外测试了10000个字符,步长100的线性数据,绘制结果如下: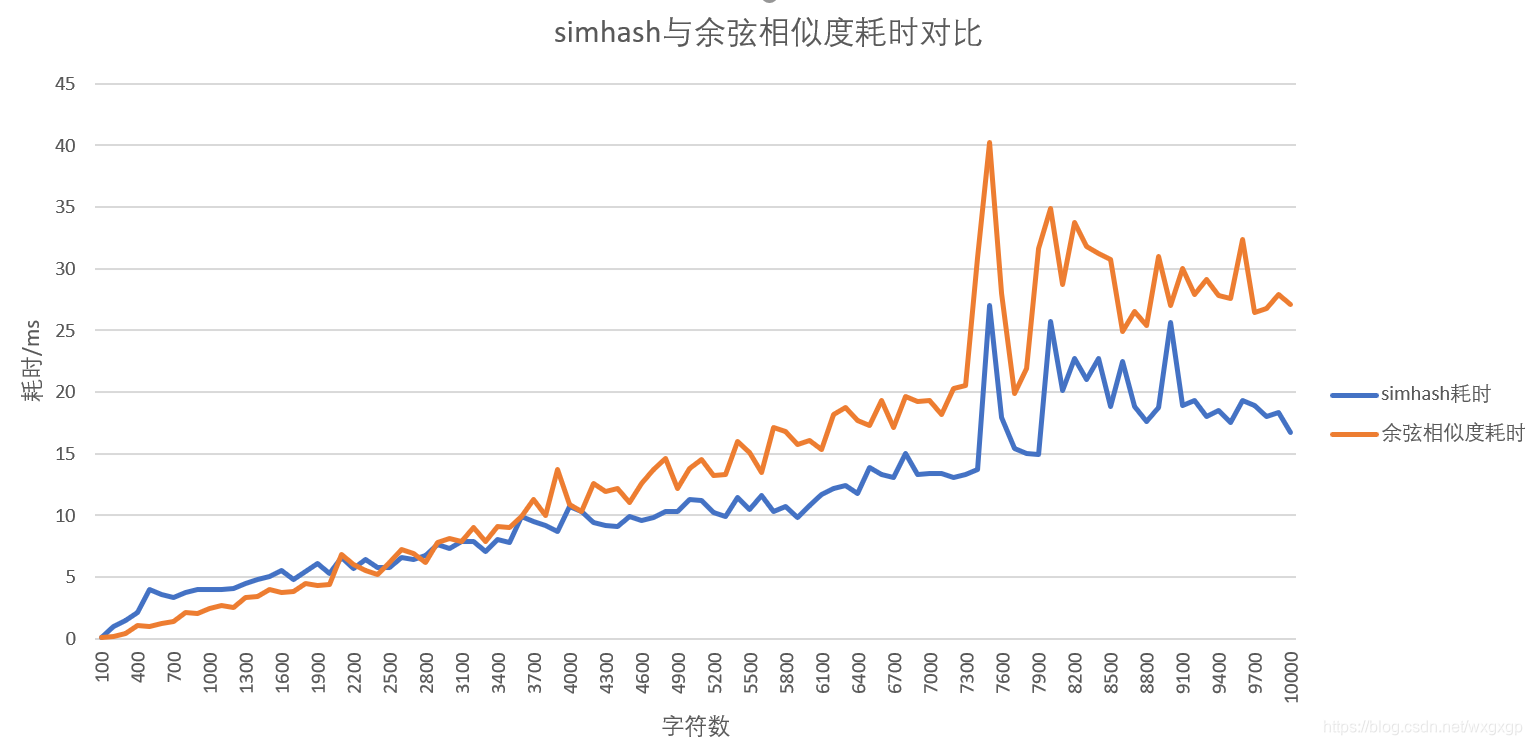
当字符数量大约大于3000时,simhash的效率高于余弦相似度的相率。(中间有段时间突增是因为启动了其他程序,占用了CPU导致的)
所以短文本使用余弦相似度来计算文本相似度还是比较适合的。而对于准确度来说,这两种方法的准确度差不多,最主要的还是取决于特征值或者的计算方式。通过简单的词频计算作为特征值,虽然简单,但是仅仅只能通过词语本身来衡量其特性,而没有语境(即上下文)来更准确的确定一个词的特征。因此也演变出了一些新的优化方法或者模型,例如TD-IDF等等,后面再陆续总结下。
All efforts, only for myself, no longer for others





























还没有评论,来说两句吧...