动态规划算法的套路，动态规划入门
前言：”与其每天担心未来，不如努力现在。别对自己丧失信心，成长的路上，只有奋斗才能给你最大的安全感“
你好，我是梦阳辰，让我们一起加油，一起努力吧！
文章目录
- 动态规划解决的问题
- 2.动态规划的算法思想
- 3.动态规划的基本步骤
- 4.经典例题讲解
1. 动态规划解决的问题
- 动态规划解决递归算法大量的冗余计算，递归算法时自顶向下思想，中间有太多重复计算，而动态规划自底向上递推求解，用表（通常为数组）记录子问题的解，以便保存和以后的检索，从最简单的问题的解填起，以自底向上的方式填表，这就保证了当我们求解一个子问题的时候，所有的与子问题相关子子问题，都可以从表中直接取用，不必重复计算。即用空间换取时间。但是，对于计算问题的解，还需利用递归公式。
- 动态规划的由来：
由于20世纪40年代末期，还没有出现计算机，这个动态填表的方法称为动态规划。
2.动态规划的算法思想
- 动态规划的思想的历史由来：
- 动态规划的总体思想：
动态规划算法与分治算法类似，其基本思想也是将待求解的问题分解成若干子问题，先求解子问题，再从子问题的解得到原问题的解。在用分治法求解时，有些子问题被重复计算了许多次。而动态规划保存已解决的子问题的答案，而在需要时再找出以求得的答案，就可以避免大量的重复计算，从而得到多项式时间算法。 - 动态规划用一个表来记录所有已解决的子问题的答案，具体的动态规划算法是多种多样的，但它们具有相同的填表方式。
- 分治算法的特征
- 如果不具备第三条特征，则可以考虑贪心算法或动态规划。
3.动态规划的基本步骤
- 1.找出最优解的性质并刻划其结构特征
- 2.递归的定义最优值
- 3.以自底向上的方式计算出最优值
- 4.根据计算最优值得到的信息构造最优解（有时可以省略）
动态规划特点：
4.经典例题讲解
题目一：机器人一次可以走1m，2m或3m。编写一个动态规划算法求机器人走n米有多少种走法。
递归求解：include
define N 4
int robotSteps(int n){
if(n==1||n==0)return 1;else if(n==2)return 2;else return robotSteps(n-1)+robotSteps(n-2)+robotSteps(n-3);
}
int main(){int n;printf("一共有%d种走法！\n",robotSteps(N));return 0;
}
动态规划求解：
#include<stdio.h>#define N 4int robotSteps(int n){int i,arr[N+1];arr[1]=1;arr[2]=2;arr[3]=4;for(i=4;i<n+1;i++){arr[i]=arr[i-1]+arr[i-2]+arr[i-3];}return arr[n];}int main(){int n;printf("一共有%d种走法！\n",robotSteps(N));return 0;}
- 题目二：
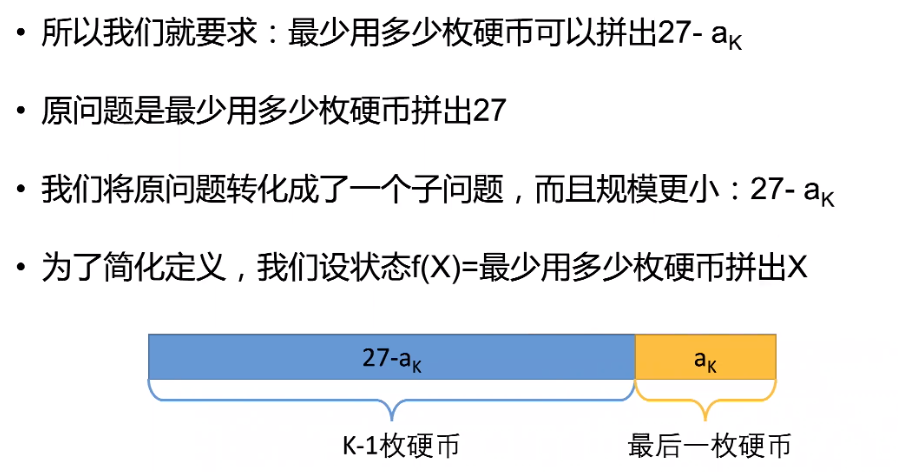
子问题：列出所有情况可能出现的最优子结构，在将这些情况找出最优子结构。
递归解法：
递归求解重复计算太多。 动态规划解决这个问题。
1.转移方程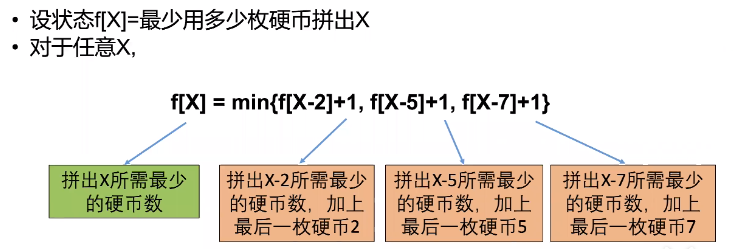
加一表示要一个硬币。
2.初始条件和边界情况
初始条件：就是用转移方程算不出来的，需要手工定义。
3.计算顺序
自顶向上，要让要求得问题，其子问题都被求过。
public static int coinChange(int []A,int M) {
int [] f =new int[M+1];int n = A.length;f[0]= 0;int i,j;for(i=1;i<=M;++i) {f[i]=Integer.MAX_VALUE;for(j=0;j<n;++j) {if(i>=A[j]&&f[i-A[j]]!=Integer.MAX_VALUE) {f[i]=Math.min(f[i]-A[j]+1,f[i]);}}
}if(f[M]==Integer.MAX_VALUE) {f[M]=-1;}return f[M];
- 题目三（计数问题）
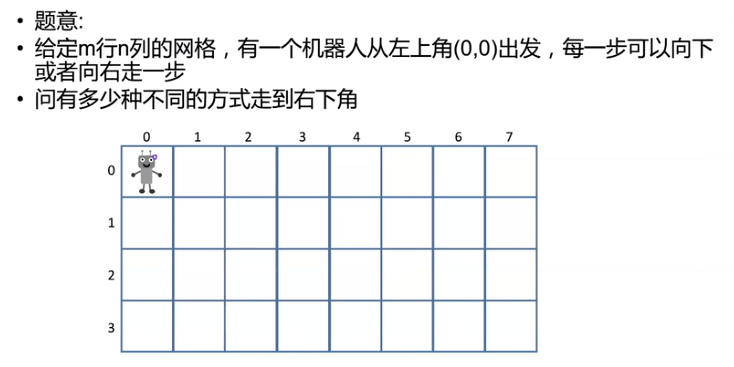
计算顺序：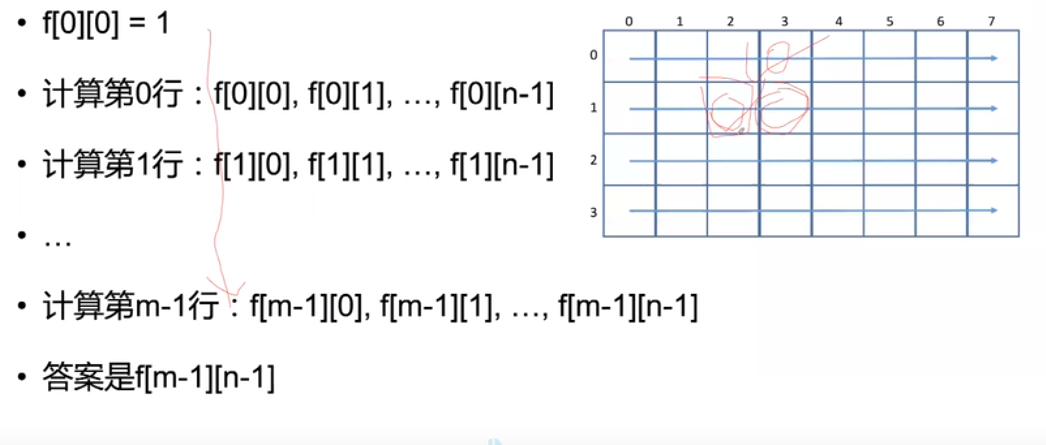
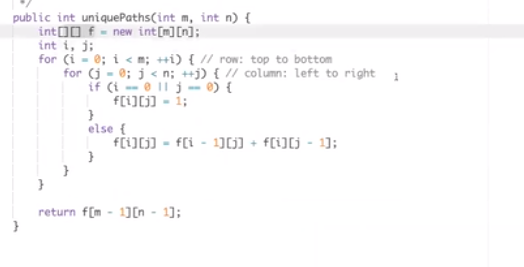
- 题目四（存在型）
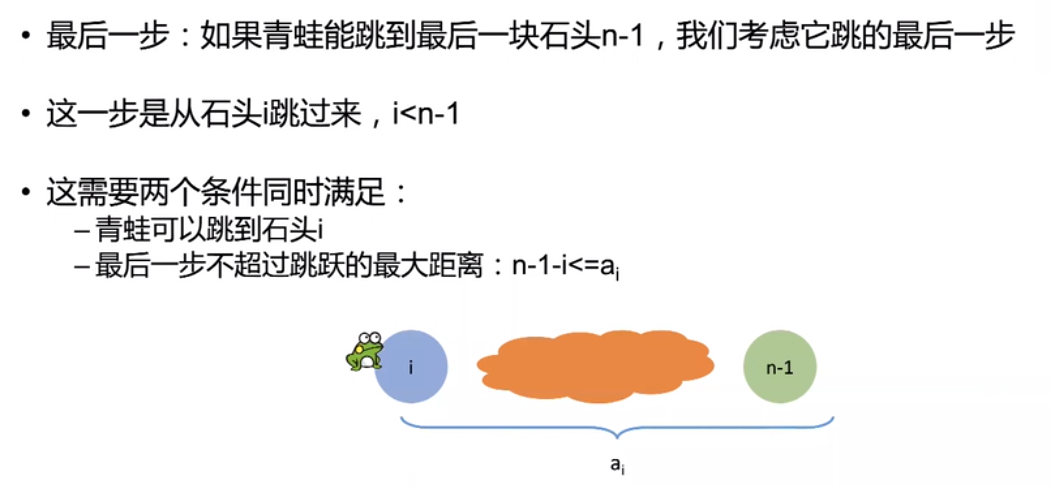
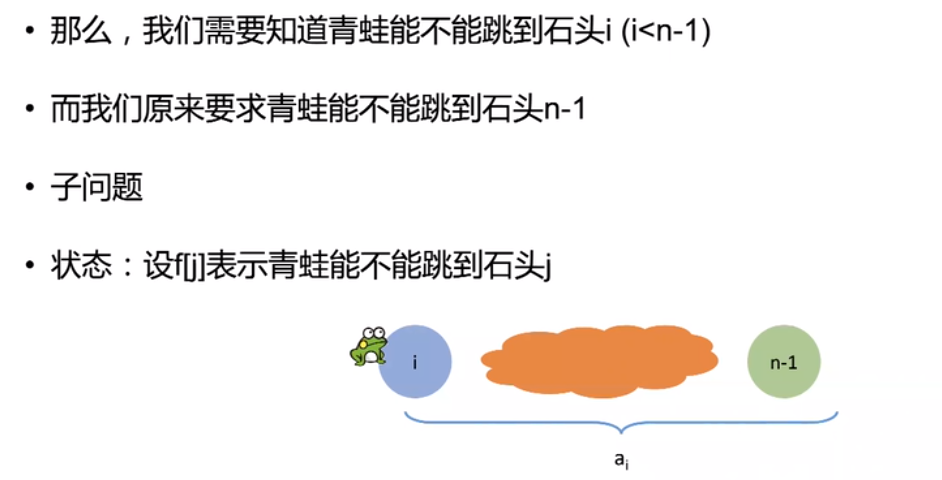
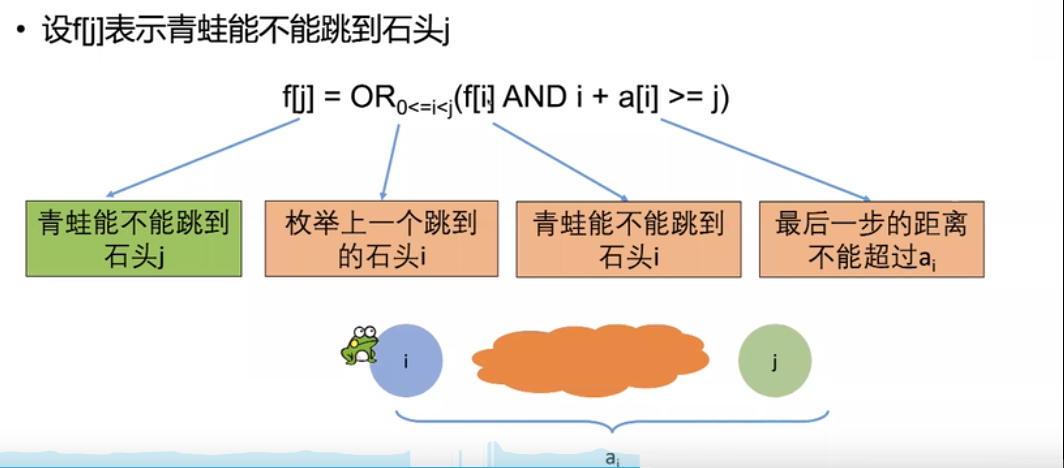
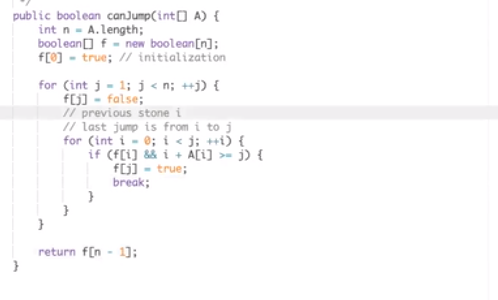
轻松搞定动态规划解决矩阵连乘问题
关注公众号【轻松玩编程】，回复“计算机资源”，“Java从入门到进阶”，获取更多学习资源！
深藏阁楼爱情的钟
短命女
爱被打了一巴掌
怼烎@
╰+哭是因爲堅強的太久メ
还没有评论，来说两句吧...