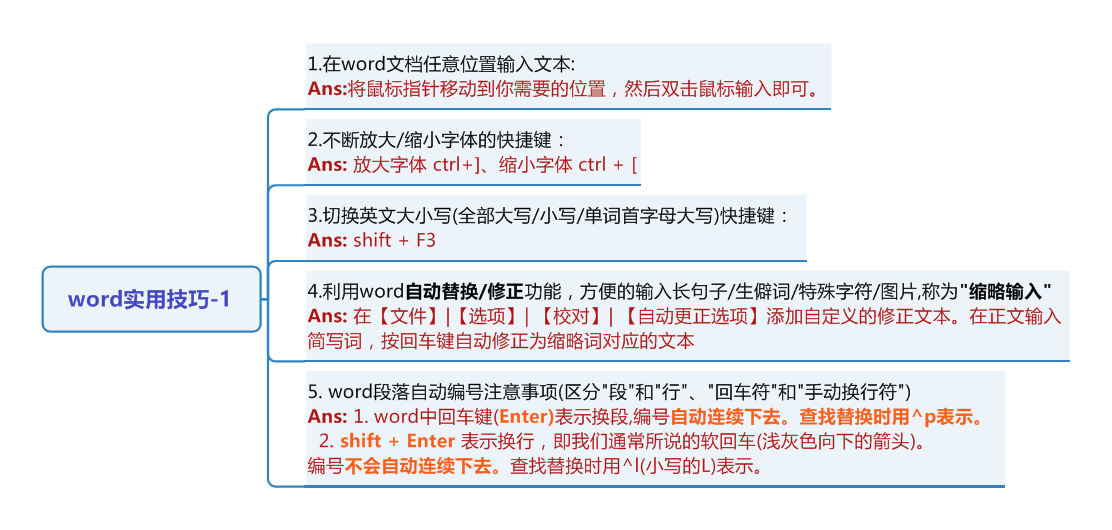
leetcode解题思路分析(二十)134 - 140题
- 加油站
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
如果题目有解,该答案即为唯一答案。
输入数组均为非空数组,且长度相同。
输入数组中的元素均为非负数。
算法
- 初始化 total_tank 和 curr_tank 为 0 ,并且选择 0 号加油站为起点。
- 遍历所有的加油站:
a. 每一步中,都通过加上 gas[i] 和减去 cost[i] 来更新 total_tank 和 curr_tank 。
b. 如果在 i + 1 号加油站, curr_tank < 0 ,将 i + 1 号加油站作为新的起点,同时重置 curr_tank = 0 ,让油箱也清空。 - 如果 total_tank < 0 ,返回 -1 ,否则返回 starting station。
想象 total_tank >= 0 的情况,同时上述算法返回 Ns作为出发加油站。算法直接保证了从 Ns 可以到达 0 ,但是剩余的路程,即从 0 到站 Ns是否有足够的油呢?如何确保从 Ns 出发可以环行一圈?我们使用 反证法可解。
class Solution {public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost){int n = gas.size();int total_tank = 0;int curr_tank = 0;int starting_station = 0;for (int i = 0; i < n; ++i){total_tank += gas[i] - cost[i];curr_tank += gas[i] - cost[i];// If one couldn't get here,if (curr_tank < 0){// Pick up the next station as the starting one.starting_station = i + 1;// Start with an empty tank.curr_tank = 0;}}return total_tank >= 0 ? starting_station : -1;}};
- 分发糖果
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
本题类似于接雨水:需要保证左右两边均满足条件,因此需要从左往右和从右往左各遍历一遍
class Solution {public:int candy(vector<int>& ratings){const int N = ratings.size();if(N == 0) return 0;if(N == 1) return 1;vector<int> left(N, 0);left[0] = 1;for(int i = 1; i < N; i++){if(ratings[i] > ratings[i - 1]){left[i] = left[i - 1] + 1;}else if(ratings[i] <= ratings[i - 1]){left[i] = 1;}}int right = 1;int s = 0;s += max(left[N - 1],right);for(int i = N - 2; i >= 0; i--){if(ratings[i] > ratings[i + 1]){right = right + 1;}else if(ratings[i] <= ratings[i + 1]){right = 1;}s += max(left[i], right);}return s;}};
- 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
线性时间复杂度 + 不能使用额外空间,所以不能用哈希表辅助解决,这里比较适合的解法是用异或做位运算。异或的特性在于同一个元素两次异或为0,0异或其他为该元素本身,因此遍历异或一遍即可
class Solution {public:int singleNumber(vector<int>& nums) {int v=0;for(int i=0; i<nums.size(); i++){v ^= nums[i];}return v;}};
- 只出现一次的数字2
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
如果其他数都出现了 kk 次,一个数出现了一次。那么如果 kk 是偶数,还是把所有的数异或起来就行了。如果 kk 是奇数,那么统计每一位是 1 的个数,然后模 kk 取余数就能得到那个单独的数了。
class Solution {public:int singleNumber(vector<int>& nums) {int once = 0, twice = 0;for (auto x : nums) {once = (once^x)&(~twice);twice = (twice^x)&(~once);}return once;}};
- 复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
解题思路:1.采取哈希表;2. 原地克隆再分离:复制节点,同时将复制节点链接到原节点后面,如A->B->C 变为 A->A’->B->B’->C->C’。设置节点random值。将复制链表从原链表分离
/* // Definition for a Node. class Node { public: int val; Node* next; Node* random; Node(int _val) { val = _val; next = NULL; random = NULL; } }; */class Solution {public:Node* copyRandomList(Node* head) {if (head == nullptr) {return head;}Node *node = head;//1. 将复制节点添加到原节点后面while (node != nullptr) {Node *copy = new Node(node->val, nullptr, nullptr);copy->next = node->next;node->next = copy;node = copy->next;}//2. 复制random节点node = head;while (node != nullptr) {if (node->random != nullptr) {node->next->random = node->random->next;}node = node->next->next;}//3. 分离链表node = head;Node *newHead = head->next;Node *newNode = newHead;while (node != nullptr) {node->next = node->next->next;if (newNode->next != nullptr) {newNode->next = newNode->next->next;}node = node->next;newNode = newNode->next;}return newHead;}};
- 单词拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
如果字符串很大,字典很大,采用Trie树或者AC自动机才是最优解,但是这里最好的选择是采用动态规划
class Solution{public:bool wordBreak(string s, vector<string>& wordDict){set<string> words;for(int i = 0; i < wordDict.size(); i++){words.insert(wordDict[i]);}vector<bool> dp(s.length() + 1);dp[0] = true;for (int i = 1; i <= s.length(); i++){for (int j = 0; j < i; j++) {if (dp[j] && words.find(s.substr(j, i - j)) != words.end() ){dp[i] = true;break;}}}return dp[s.length()];}};
- 单词拆分2
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
本题和上题基本类似,但是需要注意先检测是否存在可能性,然后再挨个存储,不然会时空超限制
class Solution {public:vector<string> wordBreak(string s, vector<string>& wordDict){if (!wordBreak_139(s, wordDict)) return { };size_t validEnd = 0;vector<vector<string>> dp(s.size() + 1, vector<string>());for (size_t i = 0; i < s.size(); i++){if (i == validEnd + 1) return { };if (i != 0 && dp[i].empty()) continue;for (auto& word : wordDict){size_t newEnd = i + word.size();if (newEnd > s.size()) continue;if (memcmp(&s[i], &word[0], word.size()) != 0) continue;validEnd = max(validEnd, newEnd);if (i == 0){dp[newEnd].push_back(word);continue;}for (auto& d : dp[i]){dp[newEnd].push_back(d + " " + word);}}}return dp.back();}bool wordBreak_139(string& s, vector<string>& wordDict){size_t validEnd = 0;vector<bool> dp(s.size() + 1, false);dp[0] = true;for (size_t i = 0; i < s.size(); i++){if (i == validEnd + 1) return false;if (!dp[i]) continue;for (auto& word : wordDict){size_t newEnd = i + word.size();if (newEnd > s.size()) continue;if (memcmp(&s[i], &word[0], word.size()) == 0){dp[newEnd] = true;validEnd = max(validEnd, newEnd);}}}return dp.back();}};
































还没有评论,来说两句吧...