图的单源最短路径(Dijkstra算法)
单源最短路径问题
如果从图中某一顶点(源点)到达另一顶点(终点)的路径可能不止一条,如何找到一条路径使得沿此路径各边上的权值总和达到最小。
Dijkstra算法由来
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
算法的具体思想
辅助数组
①采用一个path[]数组来存储路径:path[a] = b 表示最短路径中顶点a的上一顶点为b;
②采用一个info[]数组来存储各个顶点到源点的最短距离,同时此数组也有着标记的作用,即info[x]=0时,表示x顶点已经在路径中。
具体流程
①初始化辅助数组,确定源点(orign)
②使用图中的结构来对辅助数组中的最短距离进行更新:
Ⅰ、对于能到达的点:info[x] = map[orign][x];并且将这些点的前置点设为源点:path[x]=orign
Ⅱ、对于不能到达的点:info[x] = ∞
③定位info数组中权值最小(除0,0表示已加入)的点(min),取出最小权值minInfo,将该点加入路径,设置info[min]=0,并根据min顶点,对辅助数组中未加入的顶点进行更新:
若minInfo+map[min][x] < info[x],则使得info[x] = minInfo+map[min][x],并将路径中x顶点的前置顶点设置为min顶点
Ps:此步可将minInfo对应的权值大小进行存储,即源点到该点的最短路径长度。
④重复操作步骤③,直至所有顶点最短路径都得出,即数组info[]所有值都为零
输出路径
在path[]数组中存储着路径的具体信息:最短路径中当前顶点的前置路径
可使用栈的特性将其中数据取出来:
path[] = dijkstra(sMap, 1);int end = 5;//借助栈的特性int stack[] = new int[sMap.num];int top = 0;end--; //从零开始while(end != -1) {stack[top++] = end;end = path[end];}System.out.print(stack[--top]+1);while(top > 0) {//位置比索引大一System.out.print("---->"+(stack[--top]+1));}
代码实现
/*** 得出最小路径表* @param map 用二维数组存储的图结构* @return 路径数组*/public static int[] dijkstra(SimpleMap sMap,int first) {//路径数组int[] path = new int[sMap.num];//标记与权值数组(权值为0,表示已加入路径)int[] markAndInfo = new int[sMap.num];//辅助数组初始化for(int i=0; i<sMap.num; i++) {path[i] = -1;markAndInfo[i]= CreateAMap.MAX;}//定位初始位置(从零开始)first = first-1;for(int j=0; j<sMap.num; j++) {if(j != first) {path[j] = first;}markAndInfo[j]= sMap.map[first][j];}//已经加入到路径的顶点int judge = 1;while(judge < sMap.num) {//从权值数组中找出最小的的值int index = 0;int min = CreateAMap.MAX;for(int i=0; i<sMap.num; i++) {//需判断当前点是否已经在路径中if(markAndInfo[i] != 0 && markAndInfo[i] < min) {index = i;min = markAndInfo[i];}}//更新权值数组以及路径数组markAndInfo[index] = 0;for (int i = 0; i < sMap.num; i++) {if(markAndInfo[i] !=0 && min+sMap.map[index][i] < markAndInfo[i]) {markAndInfo[i] = min+sMap.map[index][i];path[i] = index;}}judge++;}return path;}
测试图及其结果: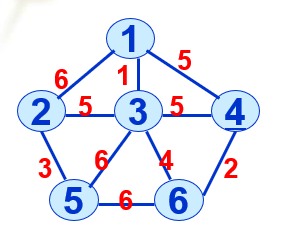
源点为1,终点为5: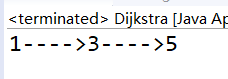































还没有评论,来说两句吧...