PTA 树的同构 (25分)-蒲公英云

PTA 树的同构 (25分)

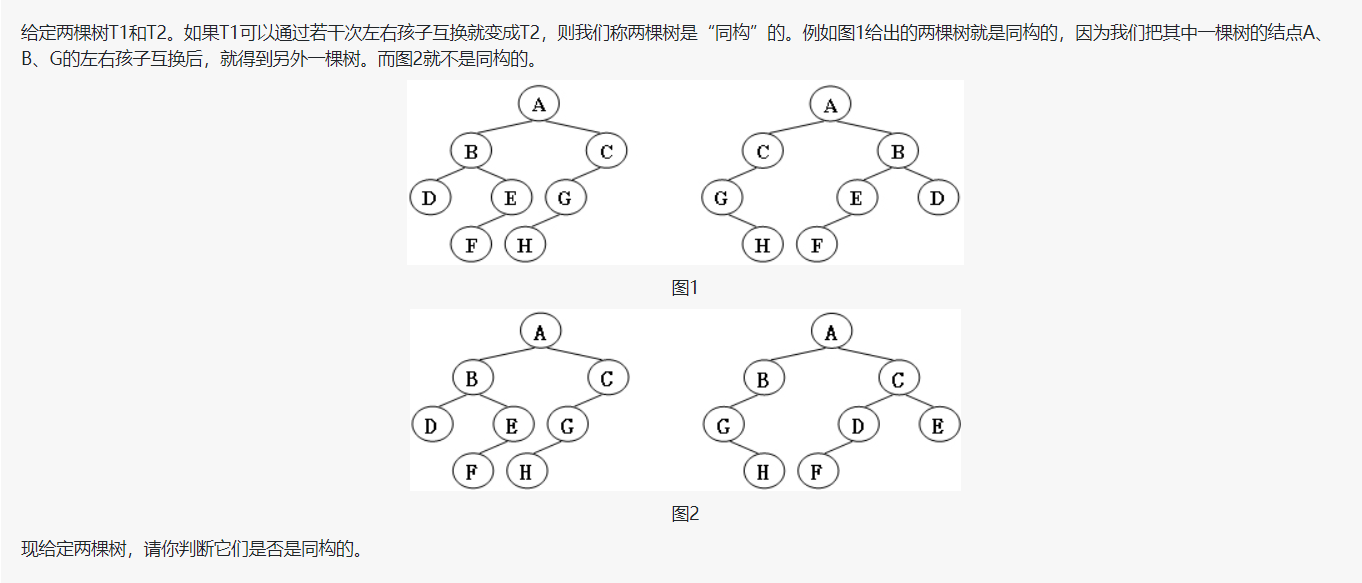
输入格式:
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。
输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

【程序思路】
首先需要根据输入找出根节点，将输入利用静态链表的方式保存，没有被指向的编号就是根节点。再调用函数递归判断树是否同构。
【程序实现】

#include<bits/stdc++.h>
using namespace std;
struct tree{
    int left,right;
    char data;
}a[15],b[15];
int getHhead(struct tree a[]) {
    int n, head = 12, check[15] = {
    0};
    cin>>n;
    getchar();
    for (int i = 0; i < n; i++) {
        string s;
        getline(cin,s);
        a[i].data = s[0];
        a[i].left = s[2] != '-' ? s[2]-'0' : 12;
        a[i].right = s[4] != '-' ? s[4]-'0' : 12;
        check[a[i].left] = 1;
        check[a[i].right] = 1;
    }
    if(n)
        for (head = 0; head < n;head++)
            if (!check[head]) break;
    return head;
}
bool jdg(int head1, int head2) {
    if(head1 == 12 && head2 == 12) 
        return true;
    else if((head1 == 12 && head2 != 12) || (head1 != 12 && head2 == 12))
        return false;
    else if(a[head1].data != b[head2].data)
        return false;
    else if(a[head1].left == 12 && b[head2].left == 12)
        return jdg(a[head1].right, b[head2].right);
    else if(a[head1].left != 12 && b[head2].left !=12 && a[a[head1].left].data == b[b[head2].left].data)
        return (jdg(a[head1].left , b[head2].left) && jdg(a[head1].right , b[head2].right));
    else
        return  jdg(a[head1].left , b[head2].right) && jdg(a[head1].right , b[head2].left);
}
int main(){
    int head1, head2;
    head1 = getHhead(a);
    head2 = getHhead(b);
    if (jdg(head1 , head2))
        cout<<"Yes\n";
    else
        cout<<"No\n";
    return 0;
}