LeetCode 100-蒲公英云

1：盛最多水的容器。

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

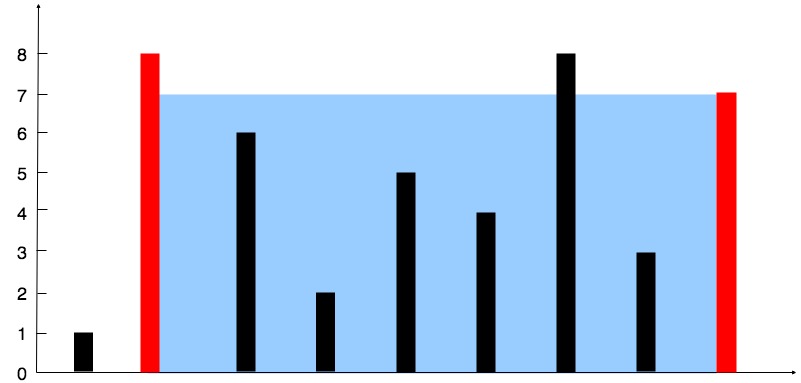
方案1：直接暴力破解，O(n*n)，但是最后会有时间限制。

方案2：双指针法，首尾指针，左指针小于右指针的值，左指针向右移动，否则右指针向左移动。终止条件是left < right。

2：三数之和。

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。注意：答案中不可以包含重复的三元组。

先排序数组，然后再利用双指针法（num[i] + num[L] + num[R]，L初始化为i+1，R初始化为n-1）。对于已经排序完了数字，那么在固定了最小数字之后，只需要管最小数字之后的两个数是否能符合条件即可。

关键点在于不能重复，1：遇到重复数字，直接跳过，当前数字等于上一个数字时。

2：不满足匹配，则相应的向前向后移动。

3：遇到满足的匹配之后，还需要继续移动L和R，L和R在往前和往后的移动过程中如果遇到相同数字，那么也需要跳过。

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        sort_array = sorted(nums)
        res = []
        for i in range(len(sort_array)-2):
            if i>0 and sort_array[i] == sort_array[i-1]:
                continue
            if sort_array[i] > 0:
                break
            left = i + 1
            right = len(sort_array) - 1
            while(left < right):
                if  sort_array[i] + sort_array[left] + sort_array[right] == 0:
                    res.append([sort_array[i], sort_array[left], sort_array[right]])
                    while(left < right and sort_array[left] == sort_array[left+1]):
                        left += 1
                    while(left < right and sort_array[right] == sort_array[right-1]):
                        right -= 1
                    left += 1
                    right -= 1
                elif sort_array[i] + sort_array[left] + sort_array[right] < 0:
                    left += 1
                else:
                    right -= 1   
        return res

3：删除链表的倒数第K个节点

类似于找到倒数第K个节点，要注意在先走K步的过程中是否为空。找到之后，要先置一个pre节点为None，在循环中用以保存第k个节点的上一个节点。

最后一个特殊情况就是，如果要删除的是第一个节点，那么这个pre节点为None，直接返回head.next即可。否则需要置pre.next = cur.next，之后再返回head。

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def removeNthFromEnd(self, head, n):
        """
        :type head: ListNode
        :type n: int
        :rtype: ListNode
        """
        if head is None:
            return head
        node = head
        for i in range(n):
            if node is None:
                return None
            else:
                node = node.next
        node_k = head
        node_k_pre = None
        while(node is not None):
            node = node.next
            node_k_pre = node_k
            node_k = node_k.next
        if node_k_pre is None:
            return head.next
        else:
            node_k_pre.next = node_k.next
        return head

4：合并两个有序链表：同剑指OFFER

5：电话号码全排列：

回溯算法：

满足回溯？从一组中选定一个数字后，再从另一组中选数字，满足递归条件

终止条件？选择的次数等于输入字符串的长度

中间状态？每一轮选择的数字的列表。直接传入 path 也可。

class Solution(object):
    def __init__(self):
        self.digit_info = {"2":['a','b','c'],
                            "3":['d','e','f'],
                            "4":['g','h','i'],
                            "5":['j','k','l'],
                            "6":['m','n','o'],
                            "7":['p','q','r','s'],
                            "8":['t','u','v'],
                            "9":['w','x','y','z']}
        self.res_array = []
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
        if digits == '':
            return []
        #额外数组用来保存当前的排列
        char_array = []
        self.perm(char_array, digits)
        return self.res_array
    def perm(self, char_array, digits):
        if len(digits) == 0:
            self.res_array.append(''.join(char_array))
            return 
        #不用考虑那么多，每次处理第一个字符就行了
        for x in self.digit_info[digits[0]]:
            char_array.append(x)
            self.perm(char_array, digits[1:])
            char_array.pop()

6：最长不重复子串

理解最关键，在做剑指offer的时候就想到了hash + 动态规划的方法，结果给记错了，还是要好好分析。

字符上一个出现位置记为-1，如果出现在hash中则记为hash中出现的最新位置，两个位置相减，如果大于上一个字符的最长不重复长度，那么只能为dp[i-1]+1, 否则取 i- j，这并不是可以简单的用min函数表达的，而是需要仔细分析，dvdf/abba。

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        if len(s) == 0:
            return 0
        char_info = {}
        res = 0
        temp = 0
        for i in range(len(s)):
            j = -1
            if s[i] in char_info:
                j = char_info[s[i]]
            if i - j > temp:
                temp = temp + 1
            else:
                temp = i - j
            char_info[s[i]] = i
            res = max(res, temp)
        return res

滑动窗口方法：初始化一个滑动窗口，遍历数组，如果新元素在滑动窗口中有值，那么滑动窗口的左边界一直往前移动，直到新元素在滑动窗口中是新的值，再将新元素放入滑动窗口。此时这个窗口就代表以当前字符结尾的最长不重复子串长度。

3. 无重复字符的最长子串

30. 串联所有单词的子串

76. 最小覆盖子串

159. 至多包含两个不同字符的最长子串

209. 长度最小的子数组

239. 滑动窗口最大值

567. 字符串的排列

632. 最小区间

727. 最小窗口子序列

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        if len(s) == 0:
            return 0
        window = []
        left = 0
        res = 0
        for right in range(len(s)):
            while(s[right] in window):
                window.remove(s[left])
                left += 1
            window.append(s[right])
            res = max(res, len(window))
        return res

7：括号匹配

使用栈来模拟括号的匹配，只入栈括号左半边，遇到括号右半边，弹出尾部元素，看是否匹配。

易错点：最后要判断栈长度，且遇到括号右半边的时候栈长度如果等于0，那么都是错误的匹配项。

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = []
        pair_info = {")":"(", "}":"{", "]":"["}
        for i in range(len(s)):
            if s[i] in ["(","[","{"]:
                stack.append(s[i])
            elif s[i] in ["}",")","]"]:
                if len(stack) == 0:
                    return False
                if pair_info[s[i]] != stack.pop():
                    return False
        if len(stack) != 0:
            return False
        return True

8：合并K个链表

方案1：额外数组+自定义排序方法

方案2：分支归并排序，再合并

方案3：python 自带最小堆 headq

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def mergeKLists(self, lists):
        """
        :type lists: List[ListNode]
        :rtype: ListNode
        """
        nodes = []
        for head in lists:
            while(head is not None):
                nodes.append(head)
                head = head.next
        def comp(node1, node2):
            if node1.val > node2.val:
                return 1
            elif node1.val < node2.val:
                return -1
            else:
                return 0
        sorted_nodes = sorted(nodes, comp)
        for i in range(len(sorted_nodes) - 1):
            sorted_nodes[i].next = sorted_nodes[i+1]
        if len(sorted_nodes) > 0:
            sorted_nodes[len(sorted_nodes)-1].next = None
            return sorted_nodes[0]
        else:
            return None

9：在排序数组中查找元素的第一个和最后一个位置

二分法进阶，如何找到一个元素最左和最右的位置？

知识点1：整数的除法，一定会舍弃最后的小数，在python中，int(3.6) = 3

知识点2：因此二分法中，如果mid = (left + right) / 2 取的是接近left的那个中间值

如果想取接近right的中间值，那么mid = (left + right + 1) / 2

知识点3：取到 mid 之后，如果 a[mid] 小于target，那么left = mid + 1，如果mid 大于target 那么right = mid - 1，如果a[mid] == target，就要看情况了，如果想取最左等于target的，那么right = mid。如果想取最右等于target的，那么 left = mid

def find_right(nums, target):
            left = 0
            right = len(nums) - 1
            while(left < right):
                mid = (left + right + 1) / 2
                if nums[mid] > target:
                    right = mid - 1
                elif nums[mid] == target:
                    left = mid
                else:
                    left = mid + 1
            return right
        def find_left(nums, target):
            left = 0
            right = len(nums) - 1
            while(left < right):
                mid = (left + right) / 2
                if nums[mid] < target:
                    left = mid + 1
                elif nums[mid] == target:
                    right = mid
                else:
                    right = mid - 1
            return left

10:接雨水

单调栈的最佳实践

11：最大子数组和

最简单的动态规划dp[i] = max(dp[i-1] + num[i], num[i])，与剑指offer一致

12：两数相加（两个链表相加）

用到了之前学到的东西：1、初始化一个节点，复制一个节点，一个用于遍历，一个用于返回。2、不需要用数组存储，直接一个add_num保存上一位到这位的进位即可。3、注意边界条件，l1 或 l2 单独比较长的话那还要继续遍历处理，类似于合并有序链表。4、最后的最后，如果进位数add_num不等于0，那么还要多加一个node表示进位。（999 + 999，最后是四位数）

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def addTwoNumbers(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        node = ListNode()
        node_temp = node
        add_num = 0
        while(l1 and l2):
            temp_num = l1.val + l2.val + add_num
            add_num = temp_num / 10
            node_temp.next = ListNode(temp_num % 10)
            node_temp = node_temp.next
            l1 = l1.next
            l2 = l2.next
        while(l1):
            temp_num = l1.val + add_num
            add_num = temp_num / 10
            node_temp.next = ListNode(temp_num % 10)
            node_temp = node_temp.next
            l1 = l1.next
        while(l2):
            temp_num = l2.val + add_num
            add_num = temp_num / 10
            node_temp.next = ListNode(temp_num % 10)
            node_temp = node_temp.next
            l2 = l2.next
        if add_num != 0:
            node_temp.next = ListNode(add_num)
        return node.next

13：两数之和

两数之和问题，一开始想的是先排序，然后双指针法，结果是想多了，人家要返回的是两个数字在原数组中的index，那么这个破坏原有index的方法是用不了了。

可以用额外空间法，利用一个hashmap，保存每个数字出现的位置，key为数组值，value为数组的index，在每一轮找完之后，再将当前数字放入到hashmap中，这样可以防止 [3,3] = 6 这种找到自己的情况。

暴力破解的话就是类似冒泡排序，双遍历即可。

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        num_map = {}
        for i in range(len(nums)):
            if num_map.get(target - nums[i]) is not None:
                return [i, num_map.get(target - nums[i])]
            num_map[nums[i]] = i

14:寻找两个正序数组的中位数

中位数定义：奇数就是中间的数，偶数的时候是中间两个数字相加的平均，相当于一个归并排序

O(log(m+n)) 解法

【第 k 小数解法】你懂了吗？ - 寻找两个正序数组的中位数 - 力扣（LeetCode） (leetcode-cn.com)

class Solution(object):
    def findMedianSortedArrays(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: float
        """
        i = 0
        j = 0
        res_array = []
        while(i < len(nums1) and j < len(nums2)):
            if nums1[i] <= nums2[j]:
                res_array.append(nums1[i])
                i += 1
            else:
                res_array.append(nums2[j])
                j += 1
        while i < len(nums1):
            res_array.append(nums1[i])
            i += 1
        while j < len(nums2):
            res_array.append(nums2[j])
            j += 1
        if len(res_array) % 2 != 0:
            return res_array[len(res_array)/2]
        else:
            return float(res_array[len(res_array)/2] + res_array[len(res_array)/2 - 1]) / 2

高效解法：

class Solution(object):
    def findMedianSortedArrays(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: float
        """
        def getKminelement(k):
            index1 = 0
            index2 = 0
            #k表示第k小的数字
            while True:
                #若一个数组走完，另外一个数组走完剩下的步即可
                if index1 == len(nums1):
                    return nums2[index2 + k - 1]
                if index2 == len(nums2):
                    return nums1[index1 + k - 1]
                #若k等于1，直接取二者最小
                if k == 1:
                    return min(nums1[index1], nums2[index2])
                #表示往前走k/2步，两个数组求第k小，分别走k/2步，但不能超过数组长度
                new_index1 = min(len(nums1)-1, index1+k/2-1)
                new_index2 = min(len(nums2)-1, index2+k/2-1)
                if nums1[new_index1] < nums2[new_index2]:
                    #由于index可能会更新为当前数组的最后一个数字，所以k更新为  k -= 跳过的步数
                    k -= new_index1 - index1 + 1
                    index1 = new_index1 + 1
                else:
                    k -= new_index2 - index2 + 1
                    index2 = new_index2 + 1
        if (len(nums1) + len(nums2)) % 2 == 1:
            return getKminelement((len(nums1) + len(nums2)+1)/2)
        else:
            return float(getKminelement(((len(nums1) + len(nums2))/2)) + \
                         getKminelement((len(nums1) + len(nums2))/2 + 1)) / 2

15：每日温度

利用单调递减栈，找到下一个最大值，当前 index - 栈中弹出的元素的 index 就是相差的天数。

class Solution(object):
    def dailyTemperatures(self, temperatures):
        """
        :type temperatures: List[int]
        :rtype: List[int]
        """
        stack = []
        res = [0 for i in temperatures]
        for i in range(len(temperatures)):
            while stack and temperatures[i] > temperatures[stack[-1]]:
                temp = stack.pop()
                res[temp] = i - temp
            stack.append(i)
        return res

16：滑动窗口最大值

方案1：构造滑动窗口。

方案2：构造单调栈。

其实也是单调栈的思路，但是有一点不一样的是，此题使用单调栈会超时，使用单调队列就可以。

猜想是因为用 stack 来 pop(0) 这个方法比较耗时间？

单调栈：

class Solution(object):
    def maxSlidingWindow(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: List[int]
        """
        stack = []
        res = []
        for i in range(len(nums)):
            for element in stack:
                if element <= i - k:
                    stack.pop(0)
            while stack and nums[i] > nums[stack[-1]]:
                stack.pop()
            stack.append(i)
            if i >= k - 1:
                res.append(nums[stack[0]])
        return res

单调队列：collections.deque() / pop() / append() / popleft()

class Solution(object):
    def maxSlidingWindow(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: List[int]
        """
        window = collections.deque()
        res = []
        for i in range(len(nums)):
            while window and nums[i] > nums[window[-1]]:
                window.pop()
            window.append(i)
            while window[0] <= i - k:
                window.popleft()
            if i >= k - 1:
                res.append(nums[window[0]])
        return res

17 下一个排列

从后往前找，找到第一个相邻 i,j 满足 a[i] < a[j]，[j, end)必然是降序序列

在[j , end)中从后往前找到第一个大于a[i] 的a[k]，交换 a[i] a[k]， [j, end)依然是降序序列

再将[j, end)转为升序排列，逆序一下即可。

比较奇怪的是，leetcode上的 Python 竟然不支持切片方法的逆序[::-1] ,所以用了 list 的 reverse()方法。

class Solution(object):
    def nextPermutation(self, nums):
        """
        :type nums: List[int]
        :rtype: None Do not return anything, modify nums in-place instead.
        """
        i = -1
        j = -1
        size = len(nums) - 1
        while(size > 0):
            if nums[size - 1] < nums[size]:
                i = size - 1
                j = size
                break
            size -= 1 
        if i == -1:
            return nums.reverse()
        size = len(nums) - 1
        while(size >= j):
            if nums[size] > nums[i]:
                nums[i], nums[size] = nums[size], nums[i]
                break
            size -= 1
        size = len(nums) - 1
        while(j < size):
            nums[j], nums[size] = nums[size], nums[j]
            j += 1
            size -= 1
        return nums

18 括号生成

这里也用到了一个栈来保存括号，右括号的个数大于左括号的个数，则不满足条件。

经典的回溯法：四问？

1：是否满足回溯法这种结构？选定一个括号之后，要在‘(’ 和 ‘)’中再选一个，以此类推，满足递归结构

2：终止条件是什么？单个‘(’ 和 ‘)’ 的个数要同时等于 n，且不能大于 n，同时满足括号匹配原则。

3：是否需要visited 数组和 begin 变量？否

4：状态变量是什么？结果是什么？状态变量 path 数组，保存当前 ‘(’ 和 ‘)’ 符号，结果是 res，保存满足条件的状态变量的合集。

class Solution(object):
    def generateParenthesis(self, n):
        """
        :type n: int
        :rtype: List[str]
        """
        res = []
        def dfs(path, left, right):
            if left == n and right == n:
                res.append(''.join(path))
                return 
            if left > n or right > n:
                return 
            if path.count(')') > path.count('('):
                return 
            if left < n:
                dfs(path + ['('], left + 1, right)
            if right < n:
                dfs(path + [')'], left, right + 1)
        path = []
        dfs(path, 0, 0)
        return res

19：最长有效括号

核心思想依然是用栈来找出匹配的括号的下标

括号匹配问题，依然利用栈来表达，栈中保存的是所有左括号的下标，遇到右括号则和左括号下标一起弹出到 res结果中，最后再对 res进行排序，排完序之后找到数据相连的最长长度即可。

class Solution(object):
    def longestValidParentheses(self, s):
        """
        :type s: str
        :rtype: int
        """
        if s == '':
            return 0
        stack = []
        res = []
        for i in range(len(s)):
            if s[i] == ')':
                if len(stack) > 0:
                    res.append(stack.pop())
                    res.append(i)
            else:
                stack.append(i)  
        left = 0
        right = 0
        max_length = 0
        res = sorted(res)
        for i in range(len(res)-1):
            if res[i] == res[i+1] - 1:
                right = i + 1
                max_length = max(max_length, right - left + 1)
            else:
                max_length = max(max_length, right - left + 1)
                left = i + 1
                right = i + 1
        return max_length

20：搜索旋转排序数组

核心思想：二分法，难点：先保证某一段区间是单调区间，判断这个 target 是否在这个区间内。

旋转数组的特性，当nums[mid] >= left (left, mid) 是递增，否则（mid， right）是递增

class Solution(object):
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        left = 0
        right = len(nums) - 1
        while(left <= right):
            mid = (left +right) / 2
            if nums[mid] == target:
                return mid
            #(left, mid)是递增
            if nums[mid] >= nums[left]:
                if target <= nums[mid] and target >= nums[left]:
                    right = mid - 1
                else:
                    left = mid + 1
            #(mid, right)是递增
            else:
                if target >= nums[mid] and target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid - 1
        return -1

21：全排列

回溯算法：

满足回溯？数组元素每一位与它后面的元素交换，满足递归的条件

终止条件？交换当位的 index 等于数组长度

中间状态？使用数组本身作为状态，要用 num[:] 将其深拷贝过去。交换完一次之后还需要复位。

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return 0
        res = []
        def dfs(index):
            if index == len(nums):
                res.append(nums[:])
            for i in range(index, len(nums)):
                nums[i], nums[index] = nums[index], nums[i]
                dfs(index + 1)
                nums[i], nums[index] = nums[index], nums[i]
        dfs(0)
        return res

22：子集

回溯算法：

满足回溯？数组中选定一个元素之后，在剩余元素中（其实是当前元素的后面的元素，因为要避免重复），可以选，也可以不选。满足递归的条件

终止条件？数组选到最后一个数字。index 元素等于数组长度-1

中间状态？使用path 数组作为状态，保存每一轮选择的数字。

class Solution(object):
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        res = []
        def dfs(path, index):
            res.append(path)
            for i in range(index, len(nums)):
                dfs(path + [nums[i]], i + 1)
        dfs([], 0)
        return res

23：旋转图像

旋转矩阵 N

方案1：如果有额外数组，可以找出规律：

第 i 行，第 j 个元素，旋转90度后，处于第 N - i - 1列的第 j 行 : a[i][j] = a[j][n-i-1]

class Solution(object):
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.
        """
        if len(matrix) == 0:
            return matrix
        n = len(matrix)
        help_matrix = [[0 for i in range(len(matrix[0]))] for j in range(len(matrix))]
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                help_matrix[j][n-i-1] = matrix[i][j]
        #leetcode 会强制检查输入 matrix，因此必须还有一层深拷贝
        matrix[:] = help_matrix
        return matrix

方案2：如果要原地旋转，那么旋转会导致四个相应的元素相互递归替换：

因此在遍历的时候也只需要处理1/4个矩阵 i< n/2 and j < n+1/2

记不住对应关系的话，直接记住 matrix[i][j] ，然后哪个元素 p旋转后可以到 i,j ? 下一个元素就是这个旋转的元素p，然后在找到可以旋转到 p 的 q元素。

matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
= matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]

哪一个元素经过旋转会到当前的 i,j 位置呢？

通过方案1的公式即可得出matrix[n - j - 1][i] -> matrix[i][j]

class Solution(object):
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.
        """
        if len(matrix) == 0: