补：PCA降维-蒲公英云

补：PCA降维

结合网上的资料，细看了两种求解PCA的方式。当进行协方差矩阵上求解特征值时，若矩阵的维数较小，则可以使用传统的求解方式，直接求出协方差矩阵的所有特征值和对应的特征向量。但是如果是用在图片方面，加入一张100*100的图片，特征维度高达10000维，协方差矩阵则是10000*10000这种级别，这将耗费的计算量呈平方级增长。面对这样一个难点，用传统方法求解不现实，因此引出奇异值分解(SVD)，利用SVD不仅可以解出PCA的解，而且无需大的计算量。奇异值分解的基本公式，其中，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，且已按大小排序。的列向量即是的特征向量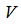；的列向量是的特征向量。在看这些数学推导的时候，感觉到自己数学基础还是很薄弱，花了不少时间去补数学知识。

PCA降维—参考文献

[1] Jon Shlens. A Tutorial on Principal Component Analysis-Derivation, Discussion and Singular Value Decomposition. 2003

[2] J. Yang, D. Zhang, A. Frangi, and J. Yang. Two-Dimensional PCA: A New Approach to Appearance-Based Face Representation and Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, no. 1, pp. 131–137, 2004.

[3] L. Sirovich and M. Kirby. Low-Dimensional Procedure for Characterization of Human Faces. J. Optical Soc. Am., vol. 4, pp. 519-524, 1987.

[4] M. Kirby and L. Sirovich. Application of the KL Procedure for the Characterization of Human Faces. IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 12, no. 1, pp. 103- 108, Jan. 1990.

[5] Zhang D, Zhou Z H. (2D)2: Two-directional two-dimensional PCA for efficient face representation and recognition[J]. Neurocomputing, 69(1):224-231,2005.

[6] G. E. Hinton, R. R. Salakhutdinov. Reducing the dimensionality of data with neural networks. Science 313 (5786): 504-507, 2006.

[7] Nawaf Hazim Barnouti. Face recognition using pca-bpnn with dct implemented on face94 and grimace databases. International Journal of Computer Applications 142(6):8-13 · May 2016

[8] Sun Y, Wang X, Tang X. Deep Learning Face Representation from Predicting 10,000 Classes[C]// IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2014:1891-1898.