1. 从 2-3 树说起

一棵标准的 BST （二叉查找树 / 二叉搜索树）是长这个样子的：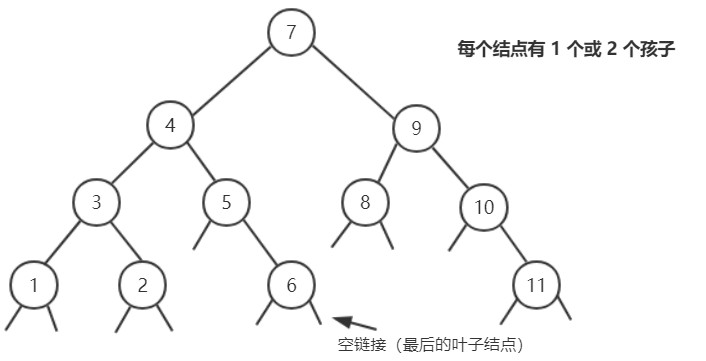
BST
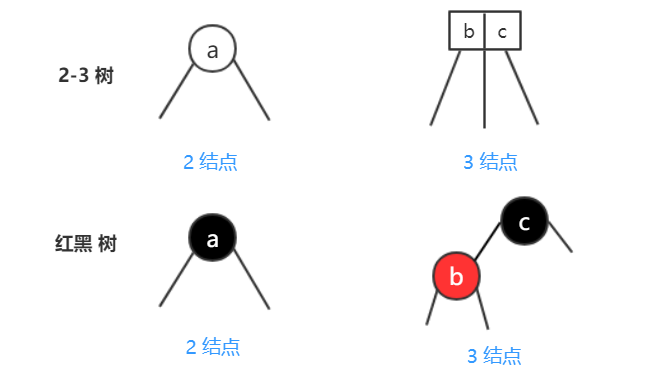
其中，这棵二叉查找树中的每个结点也叫 2-结点，2-结点就表示树中的每一个结点含有一个值和两条边，如下：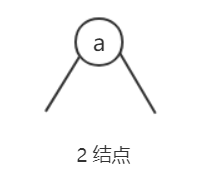
2 结点 3 结点
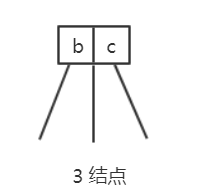
由此，引入 3-结点，3-结点就表示树中的每一个结点含有两个值和三条边（如上）

2-3 树在二分查找树的基础上多了一种 3-结点，树中的结点可以存放 1 个元素（2 个孩子），还可以存放 2 个元素（3 个孩子，此时，左孩子的值＜ b，中间孩子的值介于 b 和 c 之间，右孩子的值是＞ c 的，如上面右图所示），这就是 2-3 树名称的由来。可以看出，除了多了一种结点，2-3 树也是满足二分查找树的基本性质的。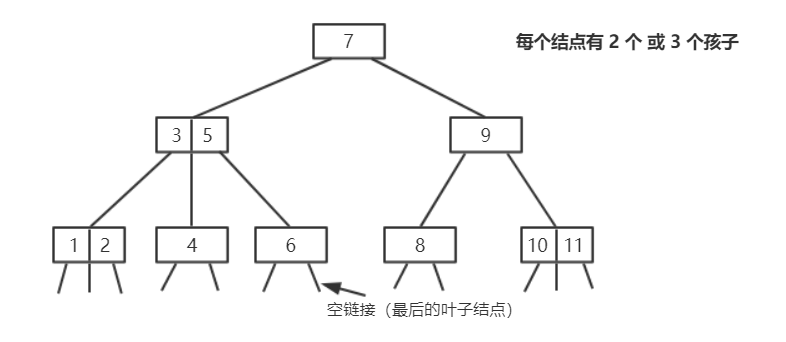
2-3 树
2-3 树是一个完全平衡的树，也就是说，2-3 树从根结点到任意一个叶子结点的距离（所经过的结点数量）一定是相同的（如上图所示）。

下面简单看下 2-3 树的查找、插入（结点）。

1.1 查找

与二叉查找树的查找思路是一样的，当查找某一个值 a 时：

先将 a 与根结点比较，如果相等，则返回；
如果 a ＜父结点的值，在其指向的左子树中继续查找；
如果 a ＞父结点的值，在其指向的右子树中继续查找；
一直指向到最后的空结点，这时返回为空。

如果查找到了 3-结点：

如果 a ＜ 3-结点的左值，则在 3-结点的左子树中继续查找；
如果 a ＞ 3-结点的右值，则在 3-结点的右子树中继续查找；
如果 a 介于 3-结点左右两个值之间，则在 3-结点的中间子树中继续查找。

1.2 插入

前面提到 2-3 树满足二叉查找树的基本性质，并且是一种绝对平衡的二叉树，那么，在添加结点的时候，必定也是以维持其绝对平衡性来执行添加操作的。

由于 2-3 树既包含 2-结点，也包含 3-结点，据此，大致可以分为两种情况讨论：

1.2.1 如果向 2-结点中插入新值

向 2-结点中插入新值

1.2.2 如果向 3-结点中插入新值

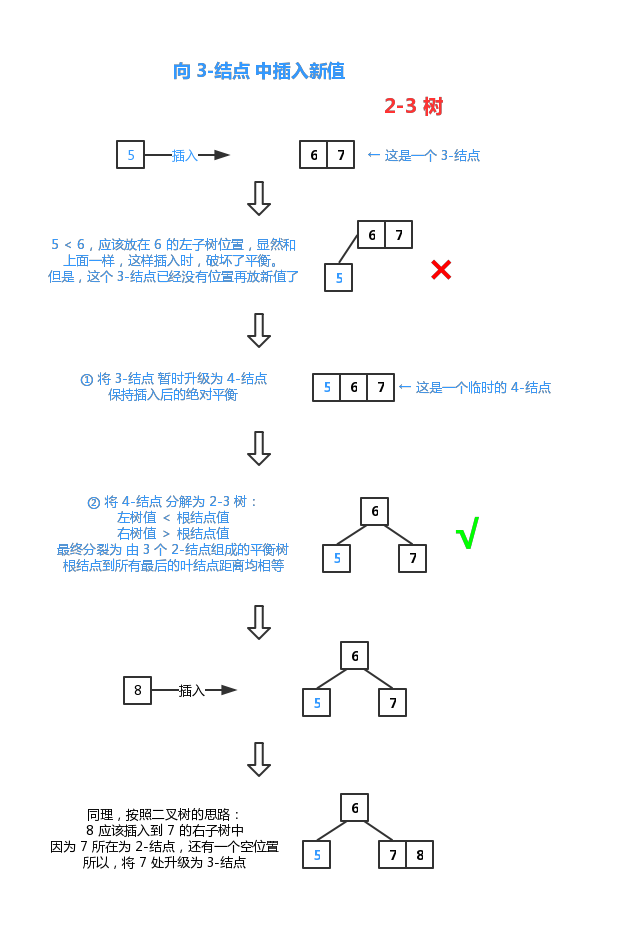
向 3-结点中插入新值
这个例子中的 2-3 树是从根结点开始“生长”的，再往下“繁衍”，又不可避免的会遇到下面这两种情景：

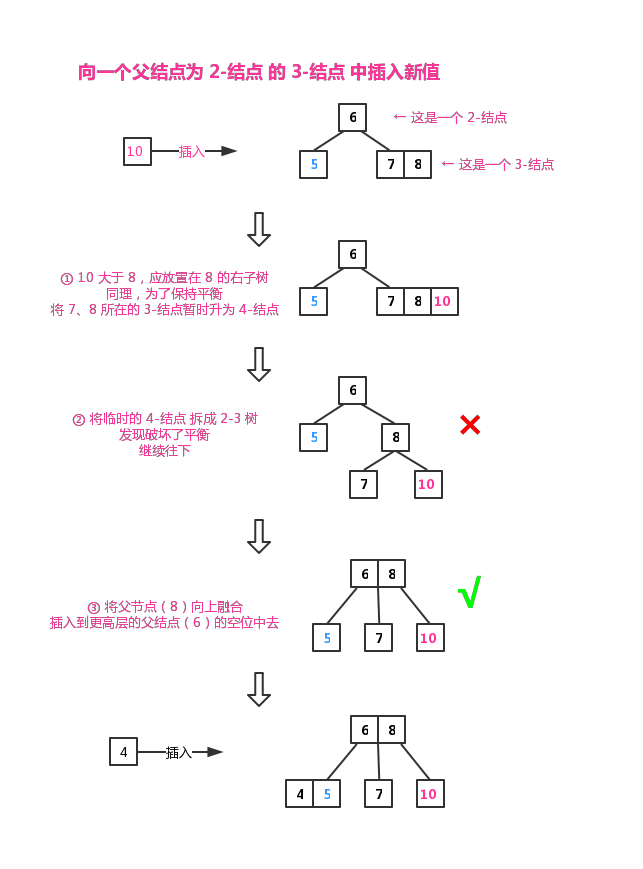
1.2.2.1 向一个父结点为 2-结点的 3-结点中插入新值

向一个父结点为 2-结点的 3-结点中插入新值

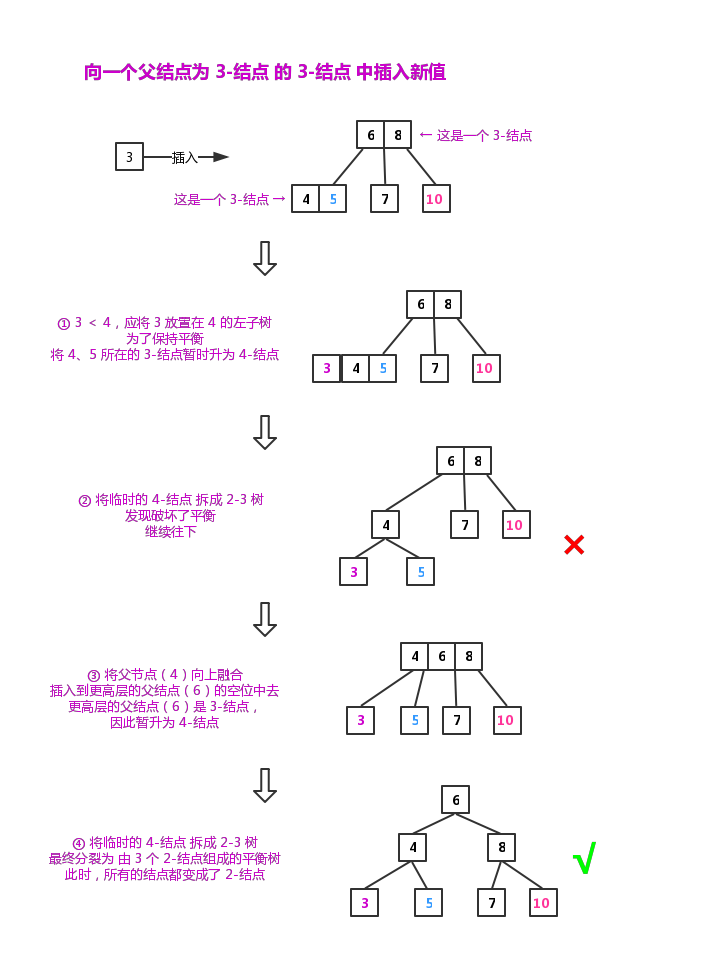
1.2.2.2 向一个父结点为 3-结点的 3-结点中插入新值

向一个父结点为 3-结点的 3-结点中插入新值

1.2.3 小结

插入思路和二分查找树类似，小于时，放在左边，大于时，放在右边。
往 2-3 树中插入元素时，不会像二分查找树那样直接新建一棵子树来放置被插入的元素，而总是在插入位置进行结点融合，使 2-结点上升为 3-结点。
插入时，始终以维持绝对平衡为目的，来进行结点的融合（2-结点上升为 3-结点、暂存为 4-结点）、4-结点拆分（成新的 2-3 子树）。

2. “红”与“黑”

2.1 从 2-3 树到红黑树

从 2-3 树到红黑树
黑色的结点其实还是一个 2-结点，红色的结点就表示它与它的父亲结点在原来的 2-3 树中是一个 3-结点，替换掉了 2-3 树中的 3-结点，这就是红黑树。

另外，从上图中 3-结点变成红色结点的过程，在原来的 2-3 树的 3- 结点中，左边的值是＜右边的值的（b ＜ c），对应成红黑树后，3-结点中的左边（b）变成了红色结点，右边（c）变成了红色结点的父结点。因此，可以看出，3-结点中的左边都是红色结点，在红黑树中，所有的红色结点都是左倾斜的。

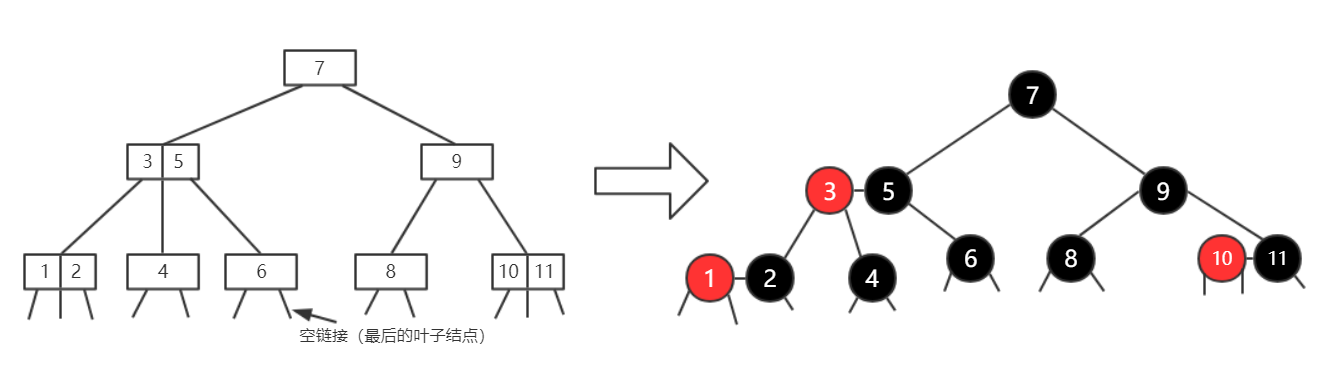
据此，在 1小节中的那棵 2-3 树所对应的红黑树，就应该是这个样子的：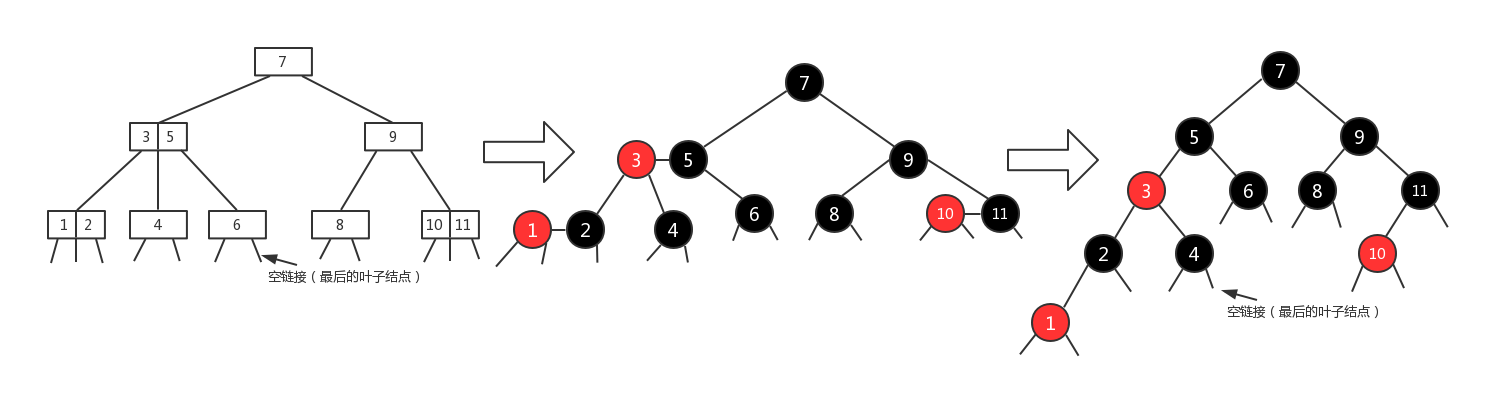
在这里插入图片描述

2.2 红黑树的性质

红黑树总是等价于 2-3 树的。
结合 2-3 树再来看红黑树的性质，可能会更加清晰：

每个结点或者是红色的，或者是黑色的。
根结点总是黑色的。
- 在 2-3 树中，根结点要么是 2-结点，要么是 3-结点。如 2.1 小节中的图示：
- 如果是 2-结点，毫无疑问，它是黑色结点。
- 如果是 3-结点，那么 3-结点中的左边元素是红色结点，右边元素是黑色结点，左边元素 < 右边元素，因此右边的元素是根结点，它是黑色的。
每一个叶子结点（最后的空结点，而不是左右子树都为空的那个结点）是黑色的。
- 它说明，在红黑树中，一个空结点是黑色的。
- 根据上条性质：根结点总是黑色的——那么一棵为空的红黑树的根结点（空结点），自然也应该是黑色的。
如果一个结点是红色的，那么它的孩子结点都是黑色的。
- 在红黑树中的红色结点，是由原来的 2-3 树中的 3-结点中左边的元素而来的。
- 而这个左边元素的孩子结点就是原来的 2-3 树中的左孩子和中间孩子。
- 不管是左孩子还是中间孩子，它要么是 2-结点，要么是 3-结点。
- 和第 2 条性质的推导一样，参考第 2 条性质中的图示。如果是 2-结点，那么红色结点连接的一点是黑色结点；如果是 3-结点，那么红色结点一定是先连接黑色节点的。
- 由这条性质，还可以推导出：如果一个结点是黑色的，那么它的右孩子一定是黑色的。
从任意一个结点到叶子结点，经过的黑色结点的数目是一样的。
- 由于 2-3 树是一棵绝对平衡的树，即，2-3 树中从任一结点出发到任意一个叶子结点的深度（所经过的结点数目）一定是相同的。
- 而 2-3 树中，只有两种结点： 2-结点和 3-结点，转化成红黑树后，这两种结点都一定会包含一个黑色结点。
- 因此，红黑树中的每一个黑色结点就象征着原来 2-3 树中一个2-结点或一个3-结点。
- 在 2-3 树中，是任一结点出发到叶子结点所经过的结点数目是相同的，那么，对应在红黑树中，就变成了：任一结点出发到叶子结点所经过的黑色结点数目是相同的 —— 有人称，红黑树是保持“黑平衡”的的二叉树（红黑树不是绝对平衡的树，它的最大高度是 2logn）。