二叉搜索树详解（Java实现）

阳光穿透心脏的1/2处 2021-06-10 20:39 573阅读 0赞

二叉搜索树定义#

二叉搜索树，是指一棵空树或者具有下列性质的二叉树：

  1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
  3. 任意节点的左，右子树也分别为二叉搜索树；
  4. 没有键值相等的节点。

用Java来表示二叉树#

  1. public class BinarySearchTree
  2. { // 二叉搜索树类
  3.     private class Node
  4.     { // 节点类
  5.         int data; // 数据域
  6.         Node right; // 右子树
  7.         Node left; // 左子树
  8.     }
  10.     private Node root; // 树根节点
  11. }

首先，需要一个节点对象的类。这个对象包含数据域和指向节点的两个子节点的引用。

其次，需要一个树对象的类。这个对象包含一个根节点root。

创建树（insert）#

  1. public void insert(int key)
  2.     {    
  3.         Node p=new Node(); //待插入的节点
  4.         p.data=key;
  6.         if(root==null)
  7.         {
  8.             root=p;
  9.         }
  10.         else
  11.         {
  12.             Node parent=new Node();
  13.             Node current=root;
  14.             while(true)
  15.             {
  16.                 parent=current;
  17.                 if(key>current.data)    
  18.                 {
  19.                     current=current.right; // 右子树
  20.                     if(current==null)
  21.                     {
  22.                         parent.right=p;
  23.                         return;
  24.                     }
  25.                 }
  26.                 else //本程序没有做key出现相等情况的处理，暂且假设用户插入的节点值都不同
  27.                 {
  28.                     current=current.left; // 左子树
  29.                     if(current==null)
  30.                     {
  31.                         parent.left=p;
  32.                         return;
  33.                     }
  34.                 }
  35.             }
  36.         }
  37.     }

创建树的时候，主要用到了parent，current来记录要插入节点的位置。哪么怎么检验自己是否正确地创建了一颗二叉搜索树呢，我们通过遍历来输出各个节点的值

遍历树（travel）#

遍历指的是按照某种特定的次序来访问二叉搜索树中的每个节点，主要有三种遍历的方法：

  1. 前序遍历，“中左右”
  2. 中序遍历，“左中右”
  3. 后续遍历，“左右中”

上面的口诀“中左右”表示的含义是，先访问根节点，再访问左子，最后访问右子。举个例子：

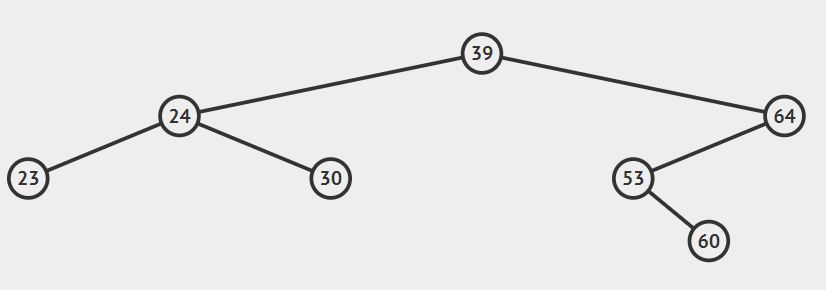
format_png

  • 前序遍历：39 24 23 30 64 53 60
  • 中序遍历：23 24 30 39 53 60 64
  • 后序遍历：23 30 24 60 53 64 39

你会发现，按照中序遍历的规则将一个二叉搜索树输入，结果为按照正序排列。

  1. public void preOrder(Node root)
  2.     { // 前序遍历,"中左右"
  3.         if (root != null)
  4.         {
  5.             System.out.print(root.data + " ");
  6.             preOrder(root.left);
  7.             preOrder(root.right);
  8.         }
  9.     }
  11.     public void inOrder(Node root)
  12.     { // 中序遍历,"左中右"
  13.         if (root != null)
  14.         {
  15.             inOrder(root.left);
  16.             System.out.print(root.data + " ");
  17.             inOrder(root.right);
  18.         }
  19.     }
  21.     public void postOrder(Node root)
  22.     { // 后序遍历,"左右中"
  23.         if (root != null)
  24.         {
  25.             postOrder(root.left);
  26.             postOrder(root.right);
  27.             System.out.print(root.data + " ");
  28.         }
  29.     }
  31.     public void traverse(int traverseType)
  32.     {    // 选择以何种方式遍历
  33.         switch (traverseType)
  34.         {
  35.         case 1:
  36.             System.out.print("preOrder traversal ");
  37.             preOrder(root);
  38.             System.out.println();
  39.             break;
  40.         case 2:
  41.             System.out.print("inOrder traversal ");
  42.             inOrder(root);
  43.             System.out.println();
  44.             break;
  45.         case 3:
  46.             System.out.print("postOrder traversal ");
  47.             postOrder(root);
  48.             System.out.println();
  49.             break;
  50.         }
  51.     }

以上的代码采用递归的方式实现三种遍历，为了方便我们使用，又写了一个traverse函数来实现选择哪种方式进行树的遍历。

这会儿就可以写单元测试了，我们首先创建一个二叉搜索树，然后分别使用“前序”，“中序”，“后序”来遍历输出树的所有节点。

  1. public static void main(String[] args)    //unit test
  2.     {    
  3.         BinarySearchTree tree=new BinarySearchTree();
  5.         tree.insert(39);
  6.         tree.insert(24);
  7.         tree.insert(64);
  8.         tree.insert(23);
  9.         tree.insert(30);
  10.         tree.insert(53);
  11.         tree.insert(60);
  13.         tree.traverse(1);
  14.         tree.traverse(2);
  15.         tree.traverse(3);
  16.     }

运行该单元测试，可以看到如下的结果：

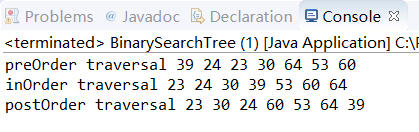
format_png 2

查找节点（find）#

  1. public Node find(int key)
  2.     { // 从树中按照关键值查找元素
  3.         Node current = root;
  4.         while (current.data != key)
  5.         {
  6.             if (key > current.data)
  7.                 current = current.right;
  8.             else
  9.                 current = current.left;
  10.             if (current == null) return null;
  11.         }
  12.         return current;
  13.     }
  15.     public void show(Node node)
  16.     {    //输出节点的数据域
  17.         if(node!=null)
  18.             System.out.println(node.data);
  19.         else
  20.             System.out.println("null");
  21.     }

查找节点比较简单，如果找到节点则返回该节点，否则返回null。为了方便在控制台输出，我们有添加了一个show函数，用来输出节点的数据域。

删除节点（delete）#

删除节点是二叉搜索树中，最复杂的一种操作，但是也不是特别难，我们分类讨论：

  • 要删除节点有零个孩子，即叶子节点

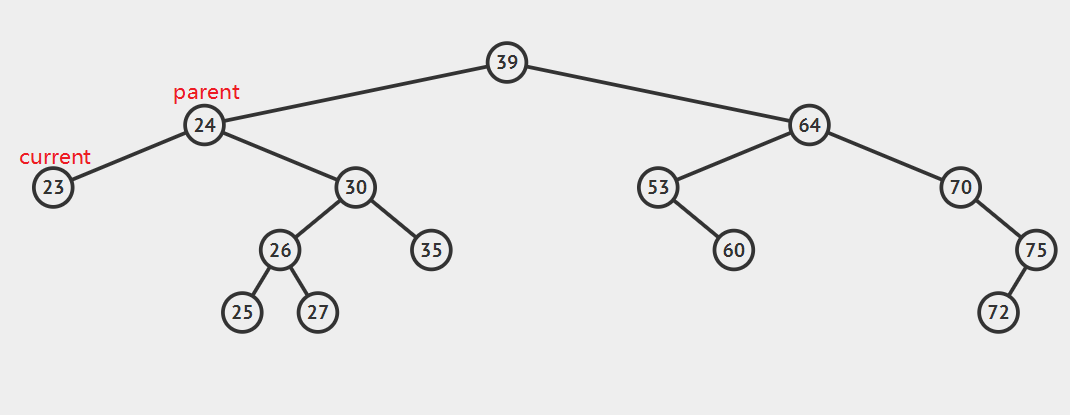
format_png 3

如图所示，只需要将parent.left(或者是parent.right)设置为null，然后Java垃圾自动回收机制会自动删除current节点。

  • 要删除节点有一个孩子

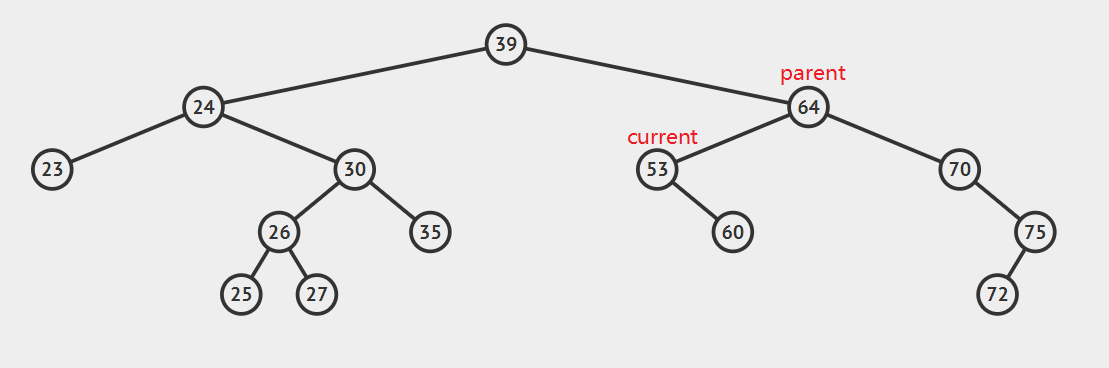
format_png 4

如图所示，只需要将parent.left(或者是parent.right)设置为curren.right(或者是current.left)即可。

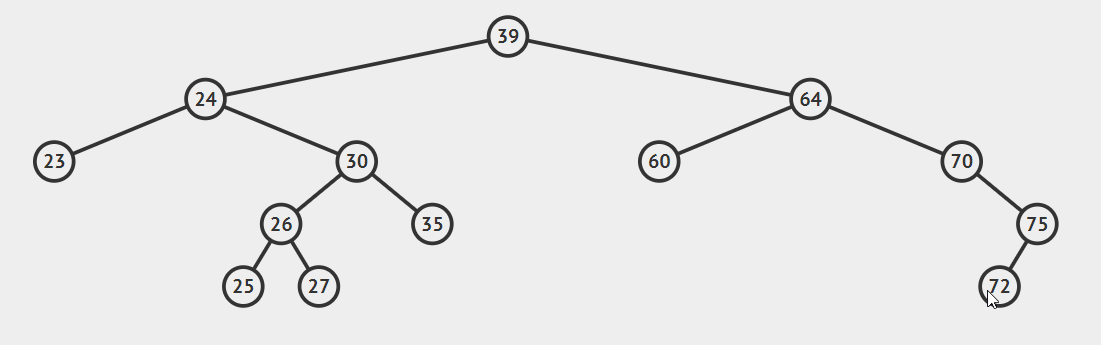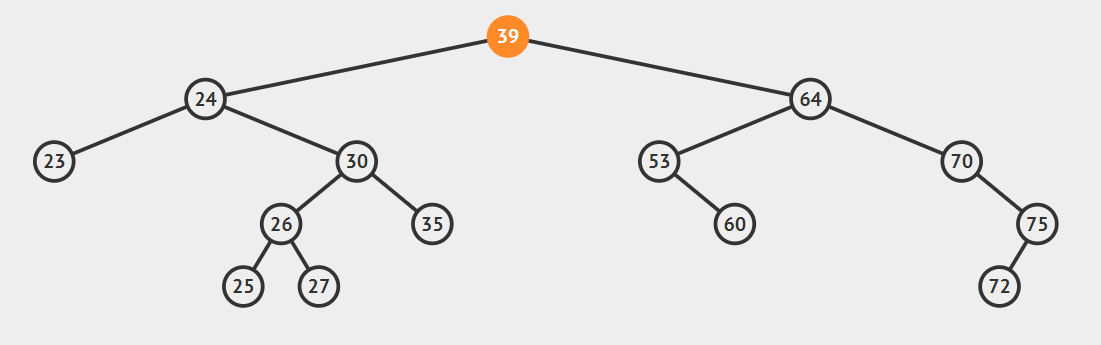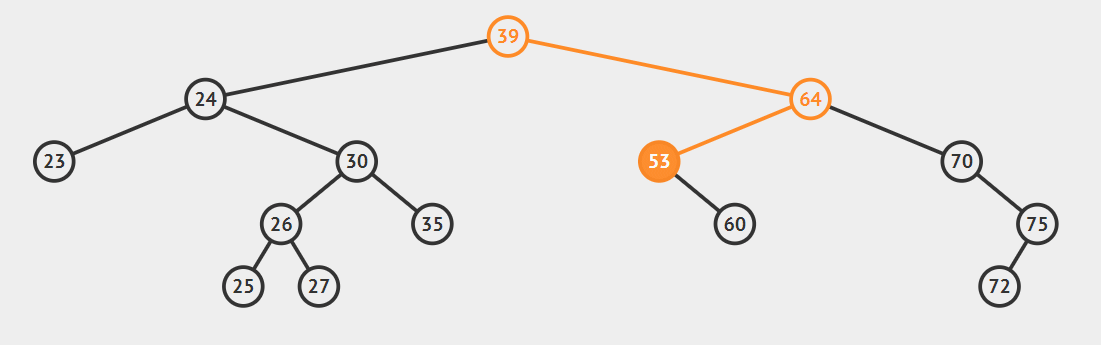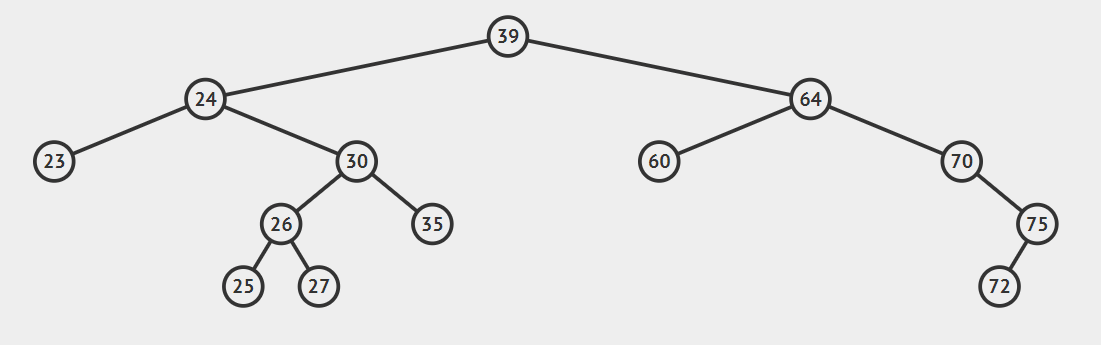
aHR0cHM6Ly9pbWcyMDE4LmNuYmxvZ3MuY29tL2Jsb2cvMTQ1OTE3OS8yMDE5MDUvMTQ1OTE3OS0yMDE5MDUwNjEyMDM0NzM5MC0xOTAwNTA0MTguZ2lm

  • 要删除节点有两个孩子

这种情况比较复杂，首先我们引入后继节点的概念，如果将一棵二叉树按照中序周游的方式输出，则任一节点的下一个节点就是该节点的后继节点。例如：上图中24的后继节点为25，64的后继节点为70.找到后继节点以后，问题就变得简单了，分为两种情况：

1.后继节点为待删除节点的右子，只需要将curren用successor替换即可，注意处理好current.left和successor.right.

注意：这种情况下，successor一定没有左孩子，一但它有左孩子，哪它必然不是current的后继节点。

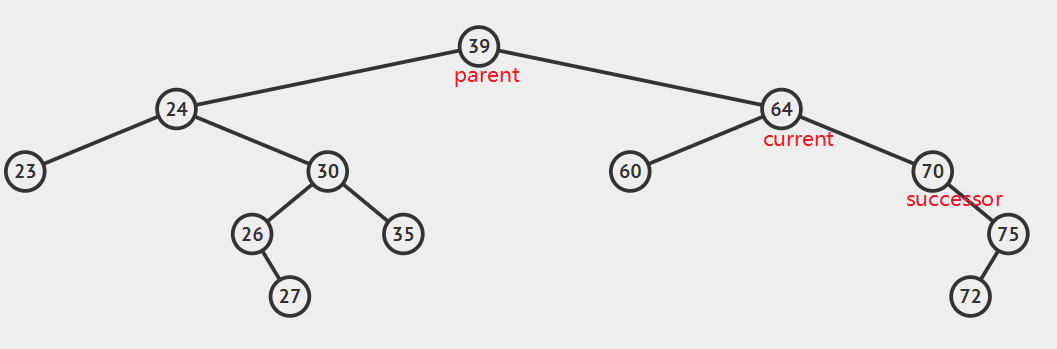
format_png 5

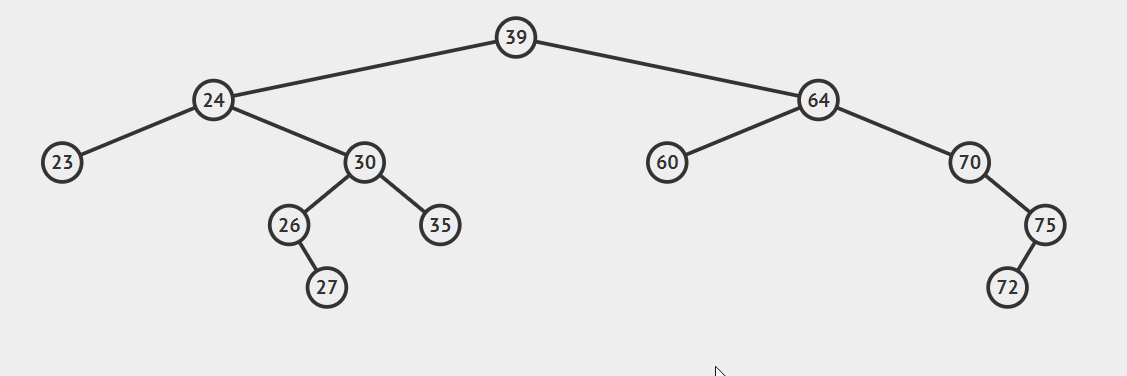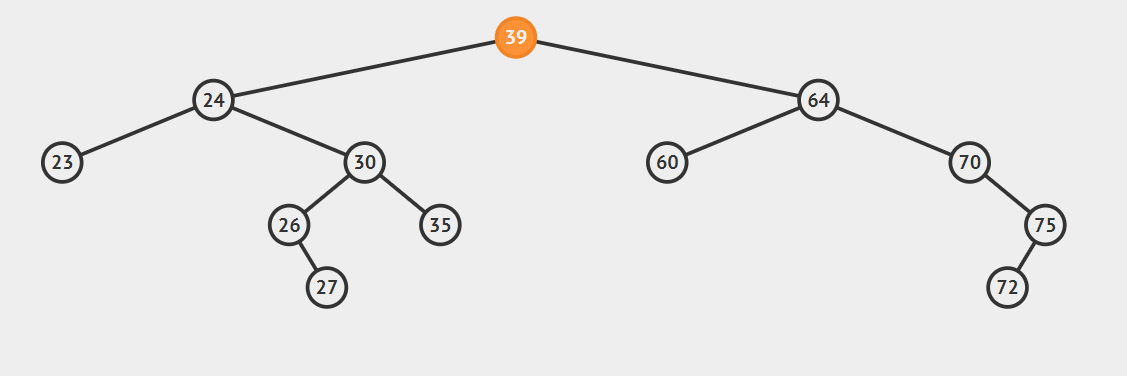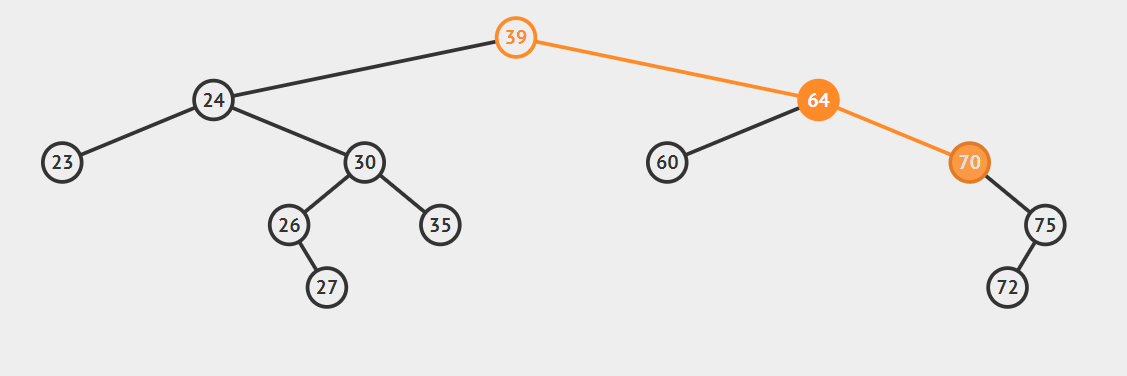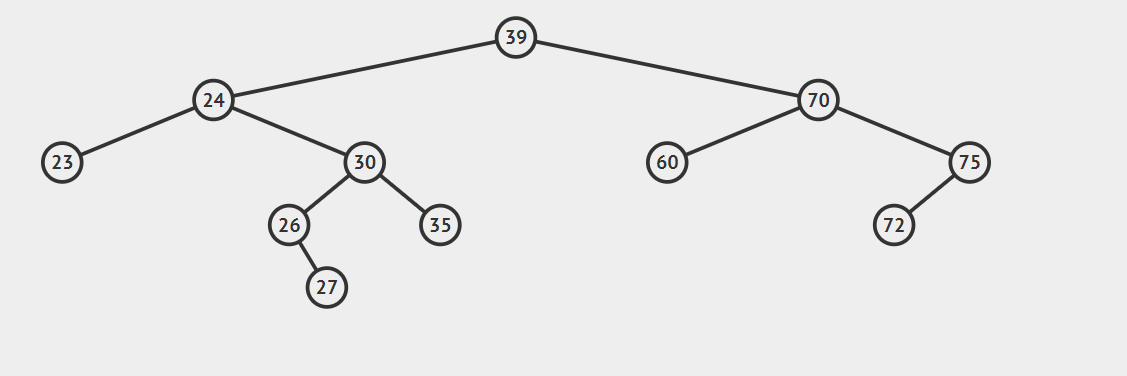
aHR0cHM6Ly9pbWcyMDE4LmNuYmxvZ3MuY29tL2Jsb2cvMTQ1OTE3OS8yMDE5MDUvMTQ1OTE3OS0yMDE5MDUwNjEzMTAxMzU3NC04MTg1NDUyMDIuZ2lm

2.后继节点为待删除结点的右孩子的左子树，这种情况稍微复杂点，请看动态图片演示。

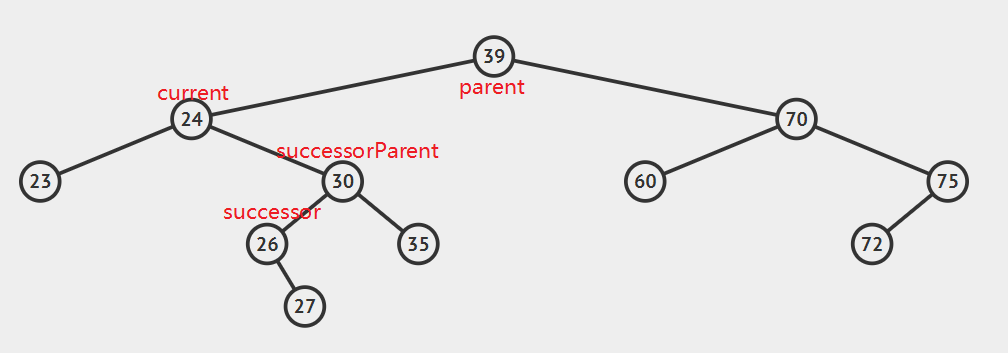
format_png 6

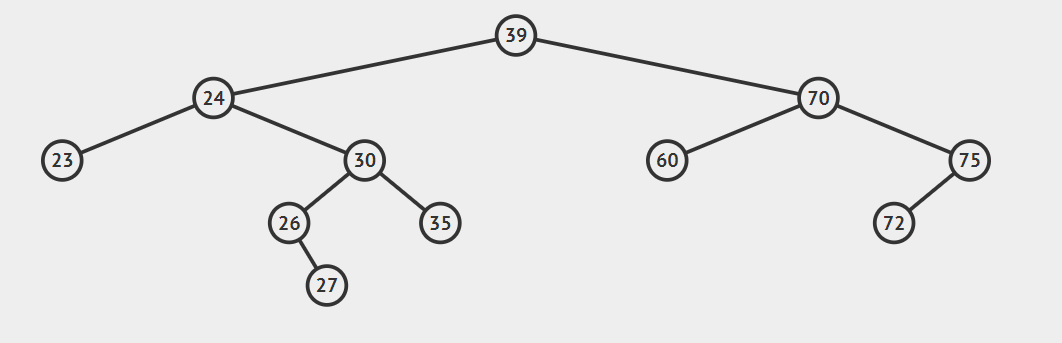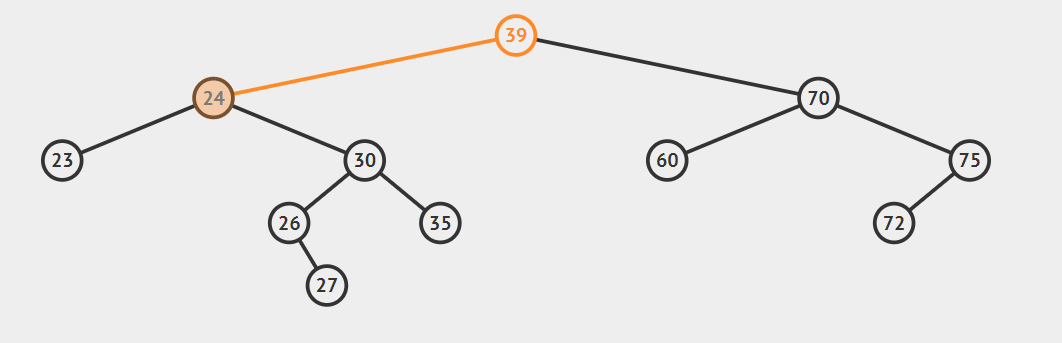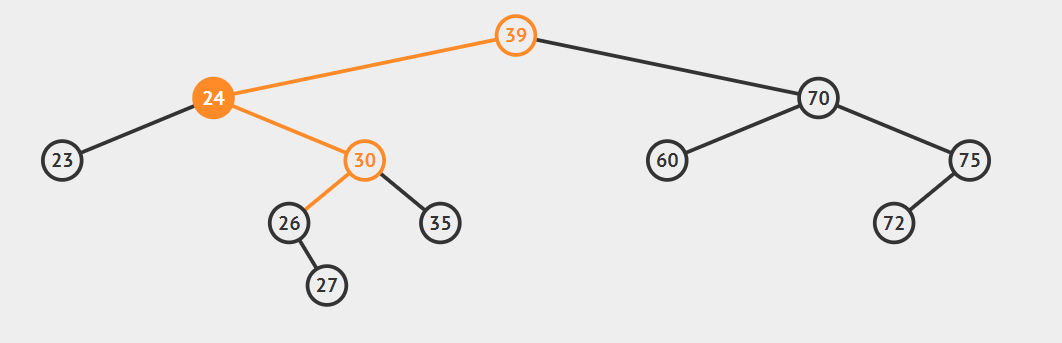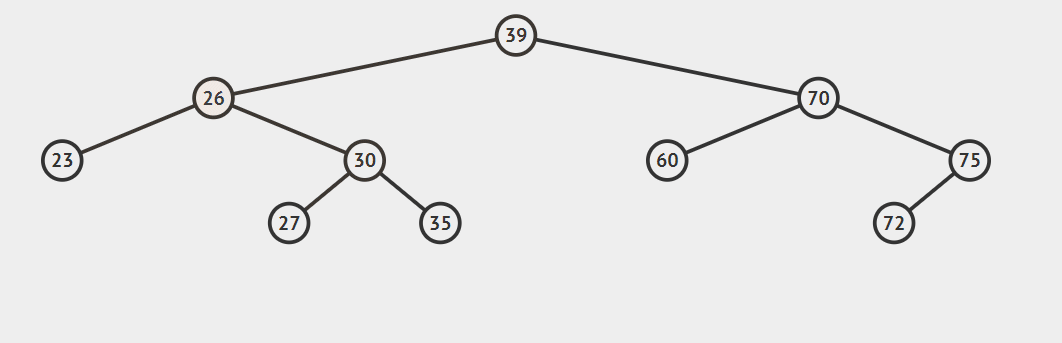
aHR0cHM6Ly9pbWcyMDE4LmNuYmxvZ3MuY29tL2Jsb2cvMTQ1OTE3OS8yMDE5MDUvMTQ1OTE3OS0yMDE5MDUwNjEzMTYzNTM2OC0xNzgxNTAyMjcxLmdpZg

算法的步骤是：

  1. successorParent.left=successor.right
  2. successor.left=current.left
  3. parent.left=seccessor

弄懂原理后，我们来看具体的代码实现：

  1. private Node getSuccessor(Node delNode)    //寻找要删除节点的中序后继结点
  2.     {
  3.         Node successorParent=delNode;
  4.         Node successor=delNode;
  5.         Node current=delNode.right;
  7.         //用来寻找后继结点
  8.         while(current!=null)
  9.         {
  10.             successorParent=successor;
  11.             successor=current;
  12.             current=current.left;
  13.         }
  15.         //如果后继结点为要删除结点的右子树的左子，需要预先调整一下要删除结点的右子树
  16.         if(successor!=delNode.right)
  17.         {
  18.             successorParent.left=successor.right;
  19.             successor.right=delNode.right;
  20.         }
  21.         return successor;
  22.     }
  24.     public boolean delete(int key) // 删除结点
  25.     {
  26.         Node current = root;
  27.         Node parent = new Node();
  28.         boolean isRightChild = true;
  29.         while (current.data != key)
  30.         {
  31.             parent = current;
  32.             if (key > current.data)
  33.             {
  34.                 current = current.right;
  35.                 isRightChild = true;
  36.             }
  37.             else
  38.             {
  39.                 current = current.left;
  40.                 isRightChild = false;
  41.             }
  42.             if (current == null) return false; // 没有找到要删除的结点
  43.         }
  44.         // 此时current就是要删除的结点,parent为其父结点
  45.         // 要删除结点为叶子结点
  46.         if (current.right == null && current.left == null) 
  47.         {
  48.             if (current == root)
  49.             {
  50.                 root = null; // 整棵树清空
  51.             }
  52.             else
  53.             {
  54.                 if (isRightChild)
  55.                     parent.right = null;
  56.                 else
  57.                     parent.left = null;
  58.             }
  59.             return true;
  60.         }
  61.         //要删除结点有一个子结点
  62.         else if(current.left==null)
  63.         {
  64.             if(current==root)
  65.                 root=current.right;
  66.             else if(isRightChild)
  67.                 parent.right=current.right;
  68.             else
  69.                 parent.left=current.right;
  70.             return true;
  71.         }
  72.         else if(current.right==null)
  73.         {
  74.             if(current==root)
  75.                 root=current.left;
  76.             else if(isRightChild)
  77.                 parent.right=current.left;
  78.             else
  79.                 parent.left=current.left;
  80.             return true;
  81.         }
  82.         //要删除结点有两个子结点
  83.         else 
  84.         {
  85.             Node successor=getSuccessor(current);    //找到要删除结点的后继结点
  87.             if(current==root)
  88.                 root=successor;
  89.             else if(isRightChild)
  90.                 parent.right=successor;
  91.             else
  92.                 parent.left=successor;
  94.             successor.left=current.left;
  95.             return true;
  96.         }
  97.     }

大家注意哪个私有函数getSuccessor的功能，它不仅仅是用来找后继结点的。

总结#

二叉搜索树其实不是特别难，理解以后，多练习几次，应该可以掌握。以下是全部的代码：

  1. package org.yahuian;
  3. public class BinarySearchTree
  4. { // 二叉搜索树类
  5.     private class Node
  6.     { // 节点类
  7.         int data; // 数据域
  8.         Node right; // 右子树
  9.         Node left; // 左子树
  10.     }
  12.     private Node root; // 树根节点
  14.     public void insert(int key)
  15.     {
  16.         Node p = new Node(); // 待插入的节点
  17.         p.data = key;
  19.         if (root == null)
  20.         {
  21.             root = p;
  22.         }
  23.         else
  24.         {
  25.             Node parent = new Node();
  26.             Node current = root;
  27.             while (true)
  28.             {
  29.                 parent = current;
  30.                 if (key > current.data)
  31.                 {
  32.                     current = current.right; // 右子树
  33.                     if (current == null)
  34.                     {
  35.                         parent.right = p;
  36.                         return;
  37.                     }
  38.                 }
  39.                 else // 本程序没有做key出现相等情况的处理，暂且假设用户插入的节点值都不同
  40.                 {
  41.                     current = current.left; // 左子树
  42.                     if (current == null)
  43.                     {
  44.                         parent.left = p;
  45.                         return;
  46.                     }
  47.                 }
  48.             }
  49.         }
  50.     }
  52.     public void preOrder(Node root)
  53.     { // 前序遍历,"中左右"
  54.         if (root != null)
  55.         {
  56.             System.out.print(root.data + " ");
  57.             preOrder(root.left);
  58.             preOrder(root.right);
  59.         }
  60.     }
  62.     public void inOrder(Node root)
  63.     { // 中序遍历,"左中右"
  64.         if (root != null)
  65.         {
  66.             inOrder(root.left);
  67.             System.out.print(root.data + " ");
  68.             inOrder(root.right);
  69.         }
  70.     }
  72.     public void postOrder(Node root)
  73.     { // 后序遍历,"左右中"
  74.         if (root != null)
  75.         {
  76.             postOrder(root.left);
  77.             postOrder(root.right);
  78.             System.out.print(root.data + " ");
  79.         }
  80.     }
  82.     public void traverse(int traverseType)
  83.     { // 选择以何种方式遍历
  84.         switch (traverseType)
  85.         {
  86.         case 1:
  87.             System.out.print("preOrder traversal ");
  88.             preOrder(root);
  89.             System.out.println();
  90.             break;
  91.         case 2:
  92.             System.out.print("inOrder traversal ");
  93.             inOrder(root);
  94.             System.out.println();
  95.             break;
  96.         case 3:
  97.             System.out.print("postOrder traversal ");
  98.             postOrder(root);
  99.             System.out.println();
  100.             break;
  101.         }
  102.     }
  104.     public Node find(int key)
  105.     { // 从树中按照关键值查找元素
  106.         Node current = root;
  107.         while (current.data != key)
  108.         {
  109.             if (key > current.data)
  110.                 current = current.right;
  111.             else
  112.                 current = current.left;
  113.             if (current == null) return null;
  114.         }
  115.         return current;
  116.     }
  118.     public void show(Node node)
  119.     {    //输出节点的数据域
  120.         if(node!=null)
  121.             System.out.println(node.data);
  122.         else
  123.             System.out.println("null");
  124.     }
  126.     private Node getSuccessor(Node delNode)    //寻找要删除节点的中序后继结点
  127.     {
  128.         Node successorParent=delNode;
  129.         Node successor=delNode;
  130.         Node current=delNode.right;
  132.         //用来寻找后继结点
  133.         while(current!=null)
  134.         {
  135.             successorParent=successor;
  136.             successor=current;
  137.             current=current.left;
  138.         }
  140.         //如果后继结点为要删除结点的右子树的左子，需要预先调整一下要删除结点的右子树
  141.         if(successor!=delNode.right)
  142.         {
  143.             successorParent.left=successor.right;
  144.             successor.right=delNode.right;
  145.         }
  146.         return successor;
  147.     }
  149.     public boolean delete(int key) // 删除结点
  150.     {
  151.         Node current = root;
  152.         Node parent = new Node();
  153.         boolean isRightChild = true;
  154.         while (current.data != key)
  155.         {
  156.             parent = current;
  157.             if (key > current.data)
  158.             {
  159.                 current = current.right;
  160.                 isRightChild = true;
  161.             }
  162.             else
  163.             {
  164.                 current = current.left;
  165.                 isRightChild = false;
  166.             }
  167.             if (current == null) return false; // 没有找到要删除的结点
  168.         }
  169.         // 此时current就是要删除的结点,parent为其父结点
  170.         // 要删除结点为叶子结点
  171.         if (current.right == null && current.left == null) 
  172.         {
  173.             if (current == root)
  174.             {
  175.                 root = null; // 整棵树清空
  176.             }
  177.             else
  178.             {
  179.                 if (isRightChild)
  180.                     parent.right = null;
  181.                 else
  182.                     parent.left = null;
  183.             }
  184.             return true;
  185.         }
  186.         //要删除结点有一个子结点
  187.         else if(current.left==null)
  188.         {
  189.             if(current==root)
  190.                 root=current.right;
  191.             else if(isRightChild)
  192.                 parent.right=current.right;
  193.             else
  194.                 parent.left=current.right;
  195.             return true;
  196.         }
  197.         else if(current.right==null)
  198.         {
  199.             if(current==root)
  200.                 root=current.left;
  201.             else if(isRightChild)
  202.                 parent.right=current.left;
  203.             else
  204.                 parent.left=current.left;
  205.             return true;
  206.         }
  207.         //要删除结点有两个子结点
  208.         else 
  209.         {
  210.             Node successor=getSuccessor(current);    //找到要删除结点的后继结点
  212.             if(current==root)
  213.                 root=successor;
  214.             else if(isRightChild)
  215.                 parent.right=successor;
  216.             else
  217.                 parent.left=successor;
  219.             successor.left=current.left;
  220.             return true;
  221.         }
  222.     }
  224.     public static void main(String[] args) // unit test
  225.     {
  226.         BinarySearchTree tree = new BinarySearchTree();
  228.         tree.insert(39);
  229.         tree.insert(24);
  230.         tree.insert(64);
  231.         tree.insert(23);
  232.         tree.insert(30);
  233.         tree.insert(53);
  234.         tree.insert(60);
  236.         tree.traverse(1);
  237.         tree.traverse(2);
  238.         tree.traverse(3);
  240.         tree.show(tree.find(23));
  241.         tree.show(tree.find(60));
  242.         tree.show(tree.find(64));
  244.         tree.delete(23);
  245.         tree.delete(60);
  246.         tree.delete(64);
  248.         tree.show(tree.find(23));
  249.         tree.show(tree.find(60));
  250.         tree.show(tree.find(64));
  251.     }
  252. }

动态图片来自于：https://visualgo.net/en/bst

发表评论

表情：
评论列表 （有 0 条评论，573人围观）

还没有评论，来说两句吧...

相关阅读

    相关 二叉搜索树实现

    本文给出二叉搜索树介绍和实现 首先说它的性质：所有的节点都满足，左子树上所有的节点都比自己小，右边的都比自己大。 那这个结构有什么有用呢？ 首先可以快速二分查找。还可以中

    傷城~傷城~/ 0 赞/ 315 阅读

    相关 java实现二叉搜索树

    二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。定义如下 > （1）若左子树不空，则左子树上所有结点的

    红太狼红太狼/ 0 赞/ 464 阅读