ACM----三角形(有n根棍子，棍子i的长度为ai。)-蒲公英云

ACM----三角形(有n根棍子，棍子i的长度为ai。)

题目：

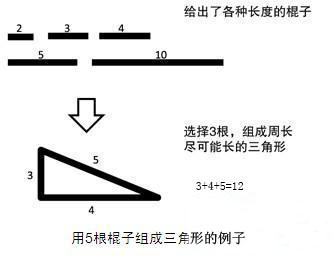
    有n根棍子，棍子i的长度为ai。想要从中选出三根棍子组成周长尽可能长的三角形。请输出最大的周长，若无法组成三角形则输出0。

限制条件

3 ≤ n ≤ 100

1 ≤ ai ≤ 10^6
输入

n = 5

a = {2,3,4,5,10}

输出

12（选择3、4、5时）

输入

n = 4

a = {4,5,10,20}

输出

0(无论怎么选都无法组成三角形)

20171019145624516

解法：

     这是《挑战程序设计竞赛(第二版)》里的一道题，书中说了一种解法O(n³)，另外，还特意说明另有一种O(nlogn)的解法，留给读者思考。下面是两种解法。
     我们知道组成三角形的充要条件是：最长的边小于其余两边之和；不难想到，可以三重循环枚举所有的选择方案，再判断能否组成三角形，最后找出最大的周长即可。
     另一种方法是先把棍子进行排序，然后只比较相邻的三个棍子，最后选择最大的周长。这样只需一次循环即可。刚开始有点不明白这种思路，后来仔细想想就明白了，那就说说我的想法，假如棍子已经升序排序了，有a <  b <  c  <  d，如果有a + b > c且a + b > d,程序中并没有比较a + b 和 d ,那么是否会漏掉这种情况导致错误呢，不会的，因为如果a + b > d的话，那么b + c 也一定 大于 d，而a + b 又小于 b + c，所以a + b 和 d后面的数的比较是多余的，这样就只需比较相邻的三个棍子即可。下面上代码。

头一种解法O（n³）：

#include<stdio.h>
int MAX(int a,int b)
{
    return a > b ? a : b;
}
int main()
{
    int a[10];
    int i,j,k,n;
    scanf("%d",&n);
    for(i = 0; i < n; i++){
        scanf("%d",&a[i]);
    }
    int ans = 0;    //答案
    //让i < j < k 这样棍子就不会被重复选取了 
    for(i = 0 ;i < n;i ++){
        for(j = i + 1;j < n;j ++){
            for(k = j + 1;k < n;k ++){
                int l = a[i] + a[j] + a[k];    //周长 
                int max = MAX(a[i],MAX(a[j],a[k]));    //找出最长的棍子 
                int rest = l - max;    //其余两根棍子的长度之和 
                //如果可以构成三角形，则更新最大周长 
                if(rest > max){
                    ans = MAX(ans,l);
                }
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

第二种解法O（nlogn）：

#include<stdio.h>
int MAX(int a,int b)
{
    return a > b ? a : b;
}
int main()
{
    int a[10];
    int i,j,t,n;
    scanf("%d",&n);
    for(i = 0; i < n; i++){
        scanf("%d",&a[i]);
    }
    //冒泡排序（升序） 
    for(i = 0 ;i < n - 1;i ++){
        for(j = 0;j < n- i -1;j ++){
            if(a[j] > a[j + 1]){
                t = a[j];
                a[j] = a[j + 1];
                a[j + 1] = t;
            }
        }
    }
    int ans = 0;    //答案
    for(i = 0 ;i < n - 2;i ++){
        int l = a[i] + a[i + 1] + a[i + 2];    //周长 
        //如果可以构成三角形，则更新最大周长 
        if(a[i] + a[i + 1] > a[i + 2]){
            ans = MAX(ans,l);
        }
    }
    printf("%d\n",ans);
    return 0;
}