[COCI2017-2018#5] Spirale

ゝ一纸荒年。 2021-10-29 23:24 161阅读 0赞

# 前言 #

祭手博客第二篇~~~

话说这道题是真的冤屈： R E RE RE，将空间从 55 55 55改到 100 100 100就 A A A了 QwQ

为什么这 20 20 20分不能加上去哇哇哇哇哇！！QAQ

# 题目 #

## 题目描述 ##

S t j e p a n Stjepan Stjepan经常和他的朋友们一起在 Z a g r e b Zagreb Zagreb的一家酒吧玩。然而， S t j e p a n Stjepan Stjepan有时会喝过多的苏打水，里面的糖会让他头晕，比如昨晚就是一个例子。而当他头晕时，脑海中始终会拥有相同的场景，这个场景是一些数字螺旋的涂鸦，但他不能完全记住这些图像的样子，但可以描述它们。

S t j e p a n Stjepan Stjepan回忆说，这个图形是一个表格，由 N N N行 M M M列的数字组成。此外，这个表格中还有 K K K个螺旋线，每个螺旋线的起点是已知的，以及它的移动方向，可以是顺时针或逆时针。螺旋通过以下方式进行：

1、最初，表格是空的，每个螺旋都在自己的初始位置。

2、随后的每一步，每个螺旋都会移动到自己的下一个位置。如果这个螺旋会离开表格边界，但也会在后面返回。

3、在完成 1 0 100 10^\{100\} 10100个步骤后，对于每个表格中的数字，是其中一个螺旋到达这个表格最早的位置。

顺逆如图： 1逆2顺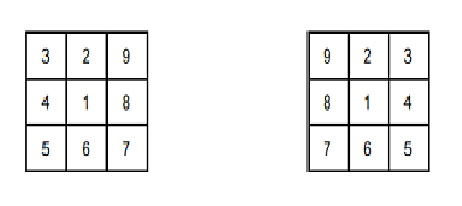  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70]

## 输入格式 ##

第一行输入三个数字 N N N（ 1 ≤ N ≤ 50 1≤N≤50 1≤N≤50）， M M M（ 1 ≤ M ≤ 50 1≤M≤50 1≤M≤50）， K K K（ 1 ≤ K ≤ N ∗ M 1≤K≤N\*M 1≤K≤N∗M）

接下来 K K K行，每行输入 3 3 3个数字，前两个数字表示螺旋的起始坐标（表格左上角坐标为( 1 , 1 1,1 1,1)），第三个数字表示螺旋的旋转方向，如果第三个数字是 0 0 0，表示是顺时针旋转，如果是1，表示是逆时针旋转。

## 输出格式 ##

输出这个 N N N行 M M M列的表格中经过螺旋的答案。题目保证螺旋的步骤不会超过 1 0 100 10^\{100\} 10100

## 样例 ##

### 样例输入1 ###

3 3 1
    2 2 0

### 样例输出1 ###

9 2 3
    8 1 4
    7 6 5

### 样例输入2 ###

3 3 1
    2 2 1

### 样例输出2 ###

3 2 9
    4 1 8
    5 6 7

### 样例输入3 ###

3 3 2
    1 1 0
    1 2 0

### 样例输出3 ###

1 1 4
    6 5 5
    19 18 17

# 解析 #

这道题开始一看到 1 0 100 10^\{100\} 10100着实吓了一跳，而且这个螺旋可以旋到外面去，这确实虚得很。。。

因此就开始推情况，将 3 ∗ 3 3\*3 3∗3的图顺时针逆时针都推了一下，一开始就成功得出了一个结论，这个螺旋线不可能超过 4 ∗ n ∗ n 4\*n\*n 4∗n∗n个。当然我不知道这对不对，因为推着推着就发现，其实这个螺旋线的边长最多即为它的出发点离这个矩阵的距离\*2+1。

也就是说如图：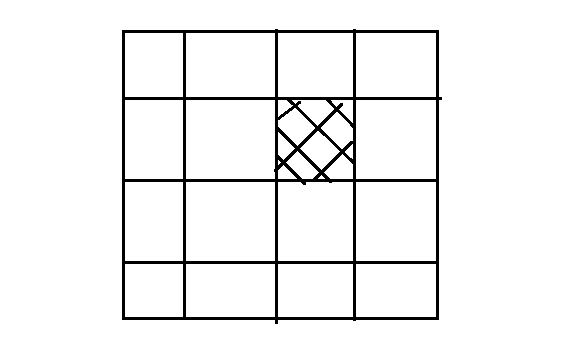  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70 1]  
在这个图中，螺旋线的起点是这个阴影点，那么如果要让它笼罩整个矩阵的话，肯定它的一半的边长是这么大：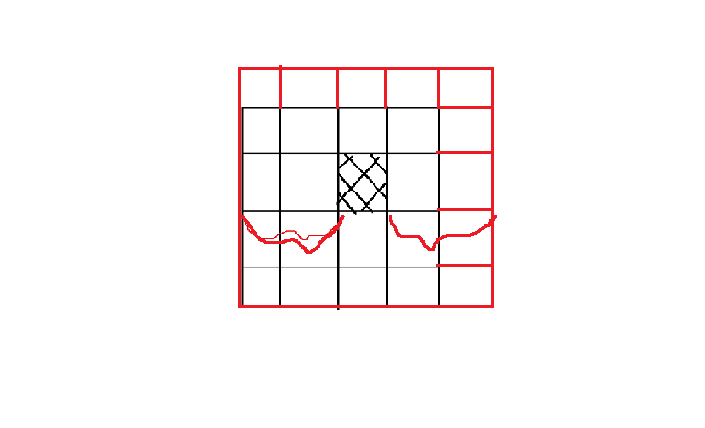  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70 2]  
在这个图上，这个螺旋线最坏的情况跑成的矩阵如图所示，即它的边长的一半就是这个点离四条边的最长距离，然后再加上这个点，总共边长即为 d i s ∗ 2 + 1 dis\*2+1 dis∗2\+1

这么推完后这个题的难点基本就没了，剩下的就是简单的二维数组基本操作了，当然要注意的是控制下标的变量不能越界，不然也会 R E RE RE

# 参考代码 #

#include <cstdio>
    #include <cmath>
    #include <cstdlib>
    #include <algorithm>
    #include <vector>
    #include <set>
    #include <map>
    #include <string>
    #include <queue>
    #include <stack>
    #include <cstring>
    #include <iostream>
    using namespace std;
    #define reg register
    #define LL long long
    #define INF 0x3f3f3f3f
    
    template<typename T>
    void re (T &x){ 
        x = 0;
        int f = 1;
        char c = getchar ();
        while (c < '0' || c > '9'){ 
            if (c == '-') f = -1;
            c = getchar ();
        }
        while (c >= '0' && c <= '9'){ 
            x = (x << 1) + (x << 3) + c - 48;
            c = getchar ();
        }
        x *= f;
    }
    
    template<typename T>
    void pr (T x){ 
        if (x < 0){ 
            putchar ('-');
            x = ~x + 1;
        }
        if (x / 10) pr (x / 10);
        putchar (x % 10 + 48);
    }
    
    int n, m, k, a[100][100];
    
    int main (){ 
        re (n); re (m); re (k);
        memset (a, INF, sizeof (a));
        while (k --){ 
            int xx, yy, ty, num, tot = 0, cnt = 1;
            re (xx); re (yy); re (ty);
            a[xx][yy] = min (a[xx][yy], num = 1);
            tot = max (tot, n - xx);
            tot = max (tot, m - yy);
            tot = max (tot, xx - 1);
            tot = max (tot, yy - 1);
            tot = (tot * 2 + 1) * (tot * 2 + 1);
            //if (xx - 1 > 0) a[xx - 1][yy] = min (a[xx - 1][yy], num = 2);
            if (ty == 1){ 
                int x = xx, y = yy;
                int flag = 0;
                while (num < tot){ 
                    int tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; x --;
                        if (x > 0 && y > 0 && y <= m) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; y --;
                        if (x > 0 && y > 0 && x <= n) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; x ++;
                        if (x <= n && x > 0 && y > 0 && y <= m) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; y ++;
                        if (x > 0 && y > 0 && y <= m && x <= n) a[x][y] = min (a[x][y], num);
                    }
                }
            }
            else{ 
                int x = xx, y = yy;
                int flag = 0;
                while (num < tot){ 
                    int tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; x --;
                        if (x > 0 && y > 0) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; y ++;
                        if (x > 0 && y > 0 && y <= m) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; x ++;
                        if (x > 0 && y > 0 && x <= n) a[x][y] = min (a[x][y], num);
                    }
                    tmp = 1; flag ++;
                    if (flag & 1) cnt ++;
                    while (tmp < cnt && num < tot){ 
                        tmp ++; num ++; y --;
                        if (x > 0 && y > 0) a[x][y] = min (a[x][y], num);
                    }
                }
            }
        }
        for (int i = 1; i <= n; i++){ 
            for (int j = 1; j <= m; j++){ 
                pr (a[i][j]);
                putchar (' ');
            }
            putchar (10);
        }
        return 0;
    }

话说为什么听他们说好像直接大模拟也能过？？不知道怎么搞的。。。

毕竟我不知道怎么判断整个矩阵到底填充完没有。。。而且就算填充完了也不一定是最小的，如果说直接模拟 2 100 2^\{100\} 2100那也太恐怖了吧， L L LL LL都没这么大、、、

果然我就是个蒟蒻 身边全是苣佬内心很受伤啊QwQ

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70]: /images/20211029/fb6de5735176464298a5a456c4a5d7f6.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70 1]: /images/20211029/716e8745e71d45ecae5ea020d5553cfc.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkyNTIzOQ_size_16_color_FFFFFF_t_70 2]: /images/20211029/3926bae31d6d4fd8ab837b08a645f05c.png