prim算法--最小生成树

悠悠 2021-11-17 02:28 436阅读 0赞

首先我们在这里先介绍一下prim算法，我记得大学数据结构先讲完最小生成树，再讲最短路径，也是考研必考问题。

prim算法在加权连通图里面寻找全局最小的生成树。是一个贪心算法。

下面两张图是我盗的哦。嘻嘻嘻

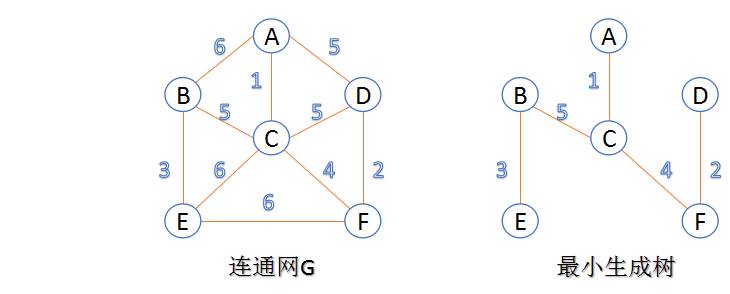
![1710133-20190609092927979-1139590534.png][]

算法：

1、输入：一个加权连通图，顶点为V的集合，边为E的集合。

将输入表示为一个二维矩阵（备注：没有连通的边的长度设为MAX）：如下

import sys
    MAX = sys.maxsize # 设置无穷大

则矩阵表示为：

primgraph = 
                [[MAX, 6, 1, 5, MAX, MAX],
                 [6, MAX, 5, MAX, 3, MAX],
                 [1, 5, MAX, 5, 6, 4],
                 [5, MAX, 5, MAX, MAX,2],
                 [MAX, 3, 6, MAX, MAX, 6],
                 [MAX, MAX, 4, 2, 6, MAX]]
    
    chararray = ['A', 'B', 'C', 'D', 'E', 'F']

初始化值：最小生成树总代价--lowcost，开辟一个数组存放最小生成树的节点

charlist.append(chararray[0])  # 存放第一个初始结点
    lowcost = []
    lowcost.append(-1)  #存放的第一个节点置为0
    sum为最小生成树的总权重

将除初始化A点的其他剩余加入lowcost初始化

for i in range(1, n):
        lowcost.append(primgraph[0][i])

开始在胜利的边缘试探

开始一次遍历

for _ in range(1, n):               # 遍历除A点之外的其他节点 
        min = MAX                       # 每次找到最小的边，min用来比较 
        minid = 0                       # 每次minid用来存放最小节点的索引
        for j in range(1, n):           # 寻找最小权重的结点，并且！=-1代表未被皇上宠幸
            if lowcost[j] != -1 and lowcost[j] < min:
                min = lowcost[j]
                minid = j
        charlist.append(chararray[minid])  # 最小生成树加入最短路径的那个节点
        sum = sum+min                      # 总权重加上剩余节点中的最短的权重
        lowcost[minid] = -1                # 则最短路径的节点刚刚被宠幸，成为过去式
        for j in range(1, n):              # 则更新宠幸名单 ，最最关键的部分！！！！
            if lowcost[j] != -1 and lowcost[j] > primgraph[minid][j]:
            #所有已经宠幸的节点，从已经宠幸的节点出发找到最短的路径，进行更新
                lowcost[j] = primgraph[mini

转载于:https://www.cnblogs.com/Victoria-happy/p/10992666.html

[1710133-20190609092927979-1139590534.png]: /images/20211116/b199860f53694920be84efe9710a8e47.png