prim算法模板—最小生成树-蒲公英云

prim算法模板—最小生成树

冷不防 2022-08-11 04:29 280阅读 0赞

    设G = (V,E)是无向连通带权图，即一个网络。E中的每一条边（v,w）的权为c\[v\]\[w\]。如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为生成树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树。构造最小生成树的两种方法：**Prim算法和Kruskal算法**。

　一、最小生成树的性质

　　设G = (V,E)是连通带权图，U是V的真子集。如果(u,v)∈E,且u∈U,v∈V-U,且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树，它意(u,v)为其中一条边。这个性质有时也称为MST性质。

　二、Prim算法（与dijkstra算法很相似）

　　设G = (V,E)是连通带权图，V = {1,2,…,n}。构造G的最小生成树Prim算法的基本思想是：首先置S = {1}，然后，只要S是V的真子集，就进行如下的贪心选择：选取满足条件i ∈S,j ∈V – S,且c[i][j]最小的边，将顶点j添加到S中。这个过程一直进行到S = V时为止。在这个过程中选取到的所有边恰好构成G的一棵最小生成树。

如下带权图：

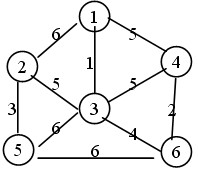
生成过程：

1 -> 3 : 1

3 -> 6 : 4

6 -> 4: 2

3 -> 2 : 5

2 -> 5 : 3

C语言代码：

void Prim(){
    int i,j,k,tmp,ans;
    for(i=1;i<=n;i++)
    dis[i]=inf;//初始化 
    dis[1]=0;
    for(i=1;i<=n;i++){
        tmp=inf;
        for(j=1;j<=n;j++){
            if(!vis[j]&&tmp>dis[j]){
                tmp=dis[j];
                k=j;
            }//找出最小距离的节点 
        }
        vis[k]=1;//把访问的节点做标记
        for(j=1;j<=n;j++){
            if(!vis[j]&&dis[j]>map[k][j])
            dis[j]=map[k][j];//更新最短距离 
        }
    }
}

三、Kruskal算法

   当图的边数为e时，Kruskal算法所需的时间是O(eloge)。当e = Ω(n^2)时，Kruskal算法比Prim算法差；但当e = o(n^2)时，Kruskal算法比Prim算法好得多。

给定无向连同带权图G = (V,E),V = {1,2,…,n}。Kruskal算法构造G的最小生成树的基本思想是：

（1）首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小大排序。

（2）从第一条边开始，依边权递增的顺序检查每一条边。并按照下述方法连接两个不同的连通分支：当查看到第k条边(v,w)时，如果端点v和w分别是当前两个不同的连通分支T1和T2的端点是，就用边(v,w)将T1和T2连接成一个连通分支，然后继续查看第k+1条边；如果端点v和w在当前的同一个连通分支中，就直接再查看k+1条边。这个过程一个进行到只剩下一个连通分支时为止。

此时，已构成G的一棵最小生成树。

Kruskal算法的选边过程：

1 -> 3 : 1

4 -> 6 : 2

2 -> 5 : 3

3 -> 4 : 4

2 -> 3 : 5