二分前缀和聪明的质检员洛谷P1314-蒲公英云

二分前缀和聪明的质检员洛谷P1314

题目链接：https://www.luogu.org/problemnew/show/P1314

题意：给出n个产品的重量w和价值v，给定m个区间，每个区间通过一个包含参数W的式子来计算，使总的值逐渐逼近一个值S

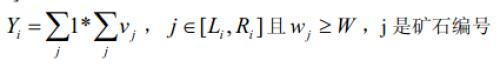
分析：很明显W为0时，所有产品都满足，此时Y最大，当W比重量w的最大值还大时，所有产品都不满足，此时Y最小，可以明显看出单调性，我们可以采用二分的方法来做

二分的话如果每次判断的话都是一个一个区间的求，时间复杂度为O(N*M),我们得用前缀和将之优化为O(N)

对于每一个W，进行前缀和的时候，如果对应的重量w比W大，则sum数组加上当前数，否则则不加。

另外，题目是要让我们尽可能的靠近标准值，所以二分的时候要另外用一个数ans来记录

这里介绍一个绝对值函数：llabs()能够求ll数的绝对值。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int maxn=2e5+7;
const ll inf=1e18+7;
const double pi=acos(-1);
ll ans=inf,res=inf;
ll n,m,s;
ll sum[maxn],sum_n[maxn],w[maxn],v[maxn],l[maxn],r[maxn];
bool isok(int x){
    ll y=0;
    memset(sum,0,sizeof(sum));
    memset(sum_n,0,sizeof(sum_n));
    for(int i=1;i<=n;i++){
        if(w[i]>=x) sum[i]=sum[i-1]+v[i],sum_n[i]=sum_n[i-1]+1;
        else sum[i]=sum[i-1],sum_n[i]=sum_n[i-1];
    }
    for(int i=0;i<m;i++){
        y+=(sum_n[r[i]]-sum_n[l[i]-1])*(sum[r[i]]-sum[l[i]-1]);
    }
    //cout<<y<<" "<<s<<endl;
    res=llabs(y-s);
    //cout<<res<<endl;
    if(s>y)return false;
    else return true;
}
int main(){
    cin>>n>>m>>s;
    ll mn=inf,mx=-1;
    for(int i=1;i<=n;i++){
        scanf("%lld%lld",&w[i],&v[i]);
        mn=min(mn,w[i]);
        mx=max(mx,w[i]);
    } 
    for(int i=0;i<m;i++){
        scanf("%d%d",&l[i],&r[i]);
    }
    int left=mn-1,right=mx+2;//右边界如果只取到mx，则包含不了所有矿石都不满足的情况,mn同理
    while(left<=right){
        int mid=(left+right)/2;
        if(isok(mid)) left=mid+1;
        else right=mid-1;
        if(res<ans) ans=res;
        //cout<<ans<<endl;
    }
    cout<<ans<<endl; 
    return 0;
}