P1314 聪明的质监员-蒲公英云

原题连接 https://www.luogu.org/problemnew/show/P1314

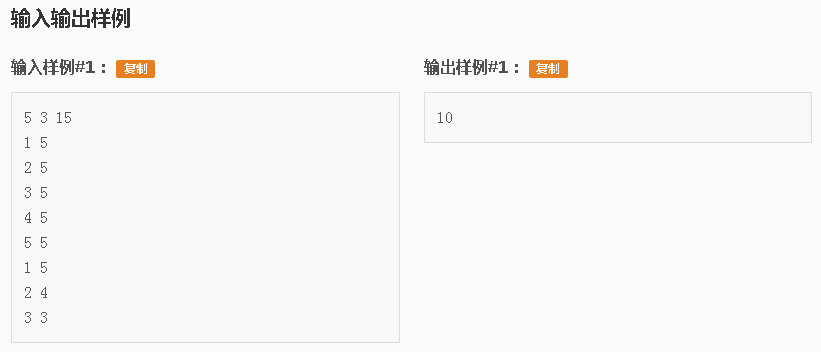
首先题号好评QwQ~ 1314

乍一看此题，发现题目好像有点难理解，先带大家理解一下吧：

意思就是：我们要在第 i 个区间 [ Li , Ri ] 里找到所有的 j，使得 wj >= W，求出这些 j 的价值总和及符合条件的 j 的个数，那么这个区间的贡献就是这个价值总和乘上 j 的个数，然后我们要算所有区间的贡献的总和 Y ，最后输出 Y - S 的绝对值的最小值，其中 W 可以自己定。

既然 W 可以自己定，那么一个很显然的思路就是我们二分枚举 W，看看哪个 W 最合适不就好啦？

枚举的上下界

我们再回头看那个公式，显然若 W 变大，则 Y 变小（符合条件的 j 的数量少了）；若 W 变小，则 Y 变大；

那么如果 W 一直变小，直到所有矿石的 wi 都大于我们枚举的这个 W 的话，那么不就是所有的矿石都被我们给选上了？这时候就会产生最大的 Y；

同理，当 W 比所有矿石的 wi 都大时，所有的矿石我们都没选，这时候就会产生最小的 Y ；

所以我们便得出来上下界：

下界：最小的 wi - 1 ；

上界：最大的 wi + 2，这里为什么是 + 2 呢？因为 + 1就是所有矿石都不选的情况，我们枚举的时候也要考虑到这种情况。所以再 + 1 就囊括了所有的情况了；

for(int i=1;i<=n;i++)
    {
        a[i].w=read();
        a[i].v=read();
        if(a[i].w>maxn_w) maxn_w=a[i].w;       //找最大重量 
        if(a[i].w<minx_w) minx_w=a[i].w;       //找最小重量 
    }
    for(int i=1;i<=m;i++)                      //m个区间 
    {
        nl[i]=read();
        nr[i]=read();
    }
    long long left=minx_w-1;                   //找上下界,这样就能包含所有情况哦 
    long long right=maxn_w+2;

二分过程

当我们枚举的 W 求出的 Y 过大时，我们应该增大 W 来使得 Y 变小来尽量接近 S；当我们枚举的 W 求出的 Y 过小时，我们应该减小 W 来使得 Y 变大来尽量接近 S；然后我们在求过过程中对 | Y - S | 一直取min 就行了。

求前缀和

最后一部分就是求每个区间的贡献，显然我们要求出每个区间符合条件的 j 的个数和价值总和，如果我们对于每个区间我们都要 O（n）的枚举一遍的话，总的时间复杂度应该是 O（nm log n），log n 是二分次数。对于 2e6 的数据，显然炸的妥妥的，那怎么办呢？

我们可以用前缀和鸭，对于我们枚举的每个 W ，我们都先预处理出价值总和，符合条件的个数这两个前缀和，然后每个区间我们 O（1）算出其贡献值，这样的时间复杂度应该是 O（（n+m） log n），比较保险~

对于上面的时间复杂度的估算，本蒟蒻很可能算错了，若发现错误请大佬们指出，感激不尽QwQ~

那么怎么求前缀和？

我们设： pre_num [ i ] 为第 1 个矿石到第 i 个矿石中符合条件的矿石数（条件：wj >= W），pre_v [ i ] 为第 1 个矿石到第 i 个矿石中所有符合条件的矿石的价值总和。

那么我们可以得出递推方程（状态转移方程）：

for(int i=1;i<=n;i++)
    {
        if(a[i].w>=W)                            //如果第i个矿石满足条件 
        {
            pre_num[i]=pre_num[i-1]+1;           //在上一个的基础上加上自己本身 
            pre_v[i]=pre_v[i-1]+a[i].v;
        }
        else                                     //不满足条件的话 
        {
            pre_num[i]=pre_num[i-1];             //继承上一个 
            pre_v[i]=pre_v[i-1];            
        }
    }

这个还是比较显然的吧QwQ~

算区间贡献

前缀和做差大家应该都会，我们有了1~n的前缀和了，那么我们求区间 [ Li , Ri ] 内的符合条件的矿石数，就是区间 [ 1 , Ri ] 内符合条件的矿石数减去区间 [ 1 , Li -1] 内符合条件的矿石数，求区间的价值总和同理：

for(int i=1;i<=m;i++)                         //m个区间
    {
        Y+=(pre_num[nr[i]]-pre_num[nl[i]-1])*(pre_v[nr[i]]-pre_v[nl[i]-1]);   //求每个区间的贡献和 
    }

上完整的AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
long long read()
{
    char ch=getchar();
    long long a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<3)+(a<<1)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
long long n,m,l,r;
long long pre_num[2000001];
long long nl[2000001],nr[2000001];
long long maxn_w,minx_w,minx,S;
long long pre_v[2000001];
struct node
{
    long long w,v;           //重量w,价值v 
}a[2000001];
int work(long long W)        //我们枚举的W 
{
    for(int i=1;i<=n;i++)
    {
        pre_num[i]=0;
        pre_v[i]=0;
    }
    for(int i=1;i<=n;i++)                        //预处理 
    {
        if(a[i].w>=W)                            //如果第i个矿石满足条件 
        {
            pre_num[i]=pre_num[i-1]+1;           //在上一个的基础上加上自己本身 
            pre_v[i]=pre_v[i-1]+a[i].v;
        }
        else                                     //不满足条件的话 
        {
            pre_num[i]=pre_num[i-1];             //继承上一个 
            pre_v[i]=pre_v[i-1];            
        }
    }
    long long Y=0;
    for(int i=1;i<=m;i++)                         //m个区间
    {
        Y+=(pre_num[nr[i]]-pre_num[nl[i]-1])*(pre_v[nr[i]]-pre_v[nl[i]-1]);   //求每个区间的贡献和 
    } 
    long long s=Y-S;
    if(s<0) s=-s;                                 //手写取绝对值,用函数总有一堆奇怪的错误
    if(s<minx) minx=s;                            //更新答案 
    if(Y>S) return 1;                             //Y太大,需要增大W来减小Y 
    if(Y<S) return 0;                             //Y太小,需要减小W来增大Y 
    if(Y==S) return -1;                           //正好,一定是最优解 
}
int main()
{
    n=read();m=read();S=read();
    maxn_w=-1314;minx_w=1e18;minx=1e18;
    for(int i=1;i<=n;i++)                       
    {
        a[i].w=read();
        a[i].v=read();
        if(a[i].w>maxn_w) maxn_w=a[i].w;       //找最大重量 
        if(a[i].w<minx_w) minx_w=a[i].w;       //找最小重量 
    }
    for(int i=1;i<=m;i++)                      //m个区间 
    {
        nl[i]=read();
        nr[i]=read();
    }
    long long left=minx_w-1;                   //找上下界,这样就能包含所有情况哦 
    long long right=maxn_w+2;
    while(left<=right)
    {
        long long mid=(left+right)>>1;
        int p=work(mid);                 
        if(p==1) left=mid+1;
        if(p==0) right=mid-1;
        if(p==-1) break;                     //找到了最优解,不必再搜了 
    }
    printf("%lld",minx);
    return 0;
}