Assigment1 k-Nearest Neighbor (kNN) exercise (1)

我不是女神ヾ 2022-01-23 03:51 146阅读 0赞

###  Assigment1 k-Nearest Neighbor (kNN) exercise (1) ###

##### 一、作业内容 #####

*  （感觉很多深度学习相关课程的入门第一课都是kNN啊。。。可能是因为它具有提高学习兴趣的魔力？或者比较简单？？）kNN分类器是一种十分简单暴力的分类器，算法原理简单易懂，就是计算距离以进行比较，它包含两个主要步骤：

###### 1）训练 ######

*  这里的训练应该加上下引号，因为它其实啥也没干，仅仅读取了训练数据并进行存储以供后续调用

###### 2）测试 ######

*  对于每一个测试样本，此课程即为测试图像，kNN将遍历一次训练集合，计算该测试图像与训练集中每一张图像的距离（暴力之处），通过排序等方法找出距离最近的k张图像，在这k张图像中，占多数的标签类别就是该测试图像所属的类别
 *  而计算图像的距离主要有两种方式，分别是曼哈顿距离（L1距离）和欧几里得距离（L2距离），具体差别如下图所示：
    
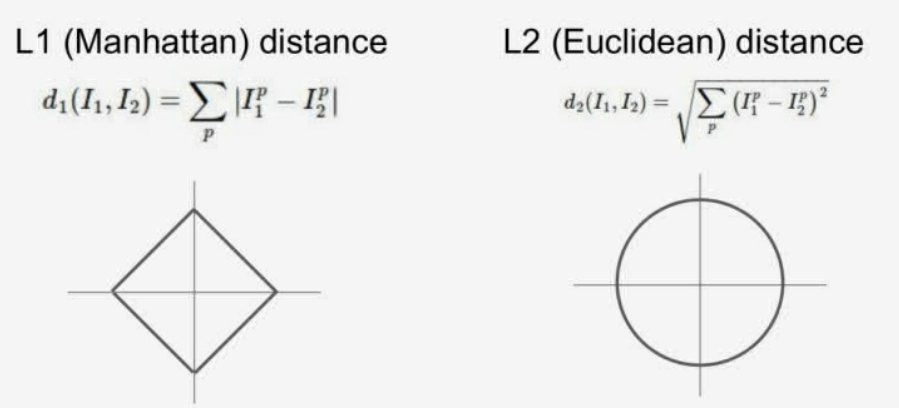
    ![iOwMHC.png][]
 *  课程中针对这两种距离计算方法进行了可视化比较，如下图所示。但是具体使用哪种距离度量就要视情况而定了，我们可以通过具体场景下的效果对比来进行探索
    
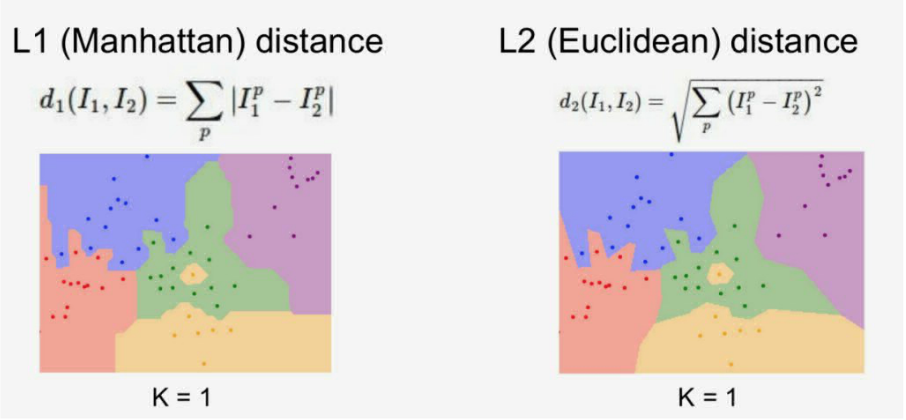
    ![gYHZEr.png][]

--------------------

##### 二、完成作业 #####

*  港真，我觉得这课的课程机制真滴好，作业的格式安排简直人性化，不会让人走弯路的感觉（个人感受）。基本上，学生要完成的工作都在py文件里，而且是通过完善函数功能的方式。然后他的notebook中已经有很多的预备代码，调用那些py文件来训练模型、测试数据等，而且notebook中还包含了大部分的说明，感觉做作业的过程是种享受。。。
 *  废话不多说，接下来就开始记录我的完成过程。首先跑一下notebook中的setup代码，主要是几个基本的配置

# Run some setup code for this notebook.
    
    import random
    import numpy as np
    from cs231n.data_utils import load_CIFAR10
    import matplotlib.pyplot as plt
    
    # This is a bit of magic to make matplotlib figures appear inline in the notebook
    # rather than in a new window.
    %matplotlib inline
    plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
    plt.rcParams['image.interpolation'] = 'nearest'
    plt.rcParams['image.cmap'] = 'gray'
    
    # Some more magic so that the notebook will reload external python modules;
    # see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
    %load_ext autoreload
    %autoreload 2

*  接下来就是加载数据，包括训练数据和测试数据（均分为X部分和Y部分）

# Load the raw CIFAR-10 data.
    cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
    
    # Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
    try:
       del X_train, y_train
       del X_test, y_test
       print('Clear previously loaded data.')
    except:
       pass
    
    X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
    
    # As a sanity check, we print out the size of the training and test data.
    print('Training data shape: ', X_train.shape)
    print('Training labels shape: ', y_train.shape)
    print('Test data shape: ', X_test.shape)
    print('Test labels shape: ', y_test.shape)

*  可以看到上述代码进行了输出，主要是输出了数据的shape，如下所示

Training data shape:  (50000, 32, 32, 3)
    Training labels shape:  (50000,)
    Test data shape:  (10000, 32, 32, 3)
    Test labels shape:  (10000,)

*  可能还对这一套数据集不熟悉？这里就将数据集中每一类的样本都随机挑选几个进行展示，代码如下：

# Visualize some examples from the dataset.
    # We show a few examples of training images from each class.
    classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
    num_classes = len(classes)
    samples_per_class = 7
    for y, cls in enumerate(classes):
        idxs = np.flatnonzero(y_train == y)
        idxs = np.random.choice(idxs, samples_per_class, replace=False)
        for i, idx in enumerate(idxs):
            plt_idx = i * num_classes + y + 1
            plt.subplot(samples_per_class, num_classes, plt_idx)
            plt.imshow(X_train[idx].astype('uint8'))
            plt.axis('off')
            if i == 0:
                plt.title(cls)
    plt.show()

*  上述代码中有个函数值得一提，即 numpy.flatnonzero() 。其最基本的功能就是输入一个矩阵，返回矩阵中非零元素的位置，如下所示：

>>> x = np.arange(-2, 3)
    >>> x
    array([-2, -1,  0,  1,  2])
    >>> np.flatnonzero(x)
    array([0, 1, 3, 4])
    
    
    import numpy as np
    d = np.array([1,2,3,4,4,3,5,3,6])
    tmp = np.flatnonzero(d == 3)
    print(tmp)
    
    [2 5 7]

*  观察上述代码中的tmp，你就能get到 idxs = np.flatnonzero(y\_train == y) 这一行代码的作用，它找出了标签中y类的位置。执行这一段可视化代码的结果如下：

![ihXF8v.png][]

*  整个数据集比较大，kNN又比较暴力，所以仅取一个子集来进行练习，代码如下

# Subsample the data for more efficient code execution in this exercise
    num_training = 5000
    mask = list(range(num_training))
    X_train = X_train[mask]
    y_train = y_train[mask]
    
    num_test = 500
    mask = list(range(num_test))
    X_test = X_test[mask]
    y_test = y_test[mask]
    
    # Reshape the image data into rows
    X_train = np.reshape(X_train, (X_train.shape[0], -1))
    X_test = np.reshape(X_test, (X_test.shape[0], -1))
    print(X_train.shape, X_test.shape)

*  接下来就要创建kNN分类器了（其实只是对训练数据进行了简单存储）。我们要做的工作主要是计算距离矩阵，如果训练样本有  N t r Ntr Ntr 个，测试样本有  N t e Nte Nte 个，则距离矩阵应该是个  N t r ∗ N t e Ntr \* Nte Ntr∗Nte 大小的矩阵，其中元素 \[i, j\] 表示第 i 个测试样本到第 j 个训练样本的距离。接下来，就是补全 k\_nearest\_neighbor.py 文件中的 compute\_distances\_two\_loops 方法，它使用粗暴的两层循环来计算测试样本与训练样本之间的距离

def compute_distances_two_loops(self, X):
            """ Compute the distance between each test point in X and each training point in self.X_train using a nested loop over both the training data and the test data. Inputs: - X: A numpy array of shape (num_test, D) containing test data. Returns: - dists: A numpy array of shape (num_test, num_train) where dists[i, j] is the Euclidean distance between the ith test point and the jth training point. """
            num_test = X.shape[0]
            num_train = self.X_train.shape[0]
            dists = np.zeros((num_test, num_train))
            for i in range(num_test):
                for j in range(num_train):
                    #####################################################################
                    # TODO: #
                    # Compute the l2 distance between the ith test point and the jth #
                    # training point, and store the result in dists[i, j]. You should #
                    # not use a loop over dimension, nor use np.linalg.norm(). #
                    #####################################################################
                    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
                    
                    dists[i][j] = np.sqrt(np.sum(np.square(X[i,:] - self.X_train[j,:])))
    
                    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            return dists

*  作业中还要求测试上述方法，并进行了可视化，但我觉得意义不大，这里就不做记录了。直接跳到下一个步骤，实现 predict\_labels 方法，以结合 compute\_distances\_two\_loops 方法进行测试样本分类

def predict_labels(self, dists, k=1):
            """ Given a matrix of distances between test points and training points, predict a label for each test point. Inputs: - dists: A numpy array of shape (num_test, num_train) where dists[i, j] gives the distance betwen the ith test point and the jth training point. Returns: - y: A numpy array of shape (num_test,) containing predicted labels for the test data, where y[i] is the predicted label for the test point X[i]. """
            num_test = dists.shape[0]
            y_pred = np.zeros(num_test)
            for i in range(num_test):
                # A list of length k storing the labels of the k nearest neighbors to
                # the ith test point.
                closest_y = []
                #########################################################################
                # TODO: #
                # Use the distance matrix to find the k nearest neighbors of the ith #
                # testing point, and use self.y_train to find the labels of these #
                # neighbors. Store these labels in closest_y. #
                # Hint: Look up the function numpy.argsort. #
                #########################################################################
                # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
                closest_y = self.y_train[np.argsort(dists[i])[:k]]
    
                # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
                #########################################################################
                # TODO: #
                # Now that you have found the labels of the k nearest neighbors, you #
                # need to find the most common label in the list closest_y of labels. #
                # Store this label in y_pred[i]. Break ties by choosing the smaller #
                # label. #
                #########################################################################
                # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
                y_pred[i] = np.argmax(np.bincount(closest_y))
    
                # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
            return y_pred

*  值得一提的是 numpy.bincount 函数，这里需要记录前k个训练样本中没中类别出现的次数，而 numpy.bincount 函数就能优雅的完成这一任务，下面给出两个例子你就懂了：

# 我们可以看到x中最大的数为7，因此bin的数量为8，那么它的索引值为0->7
    x = np.array([0, 1, 1, 3, 2, 1, 7])
    # 索引0出现了1次，索引1出现了3次......索引5出现了0次......
    np.bincount(x)
    #因此，输出结果为：array([1, 3, 1, 1, 0, 0, 0, 1])
    
    # 我们可以看到x中最大的数为7，因此bin的数量为8，那么它的索引值为0->7
    x = np.array([7, 6, 2, 1, 4])
    # 索引0出现了0次，索引1出现了1次......索引5出现了0次......
    np.bincount(x)
    #输出结果为：array([0, 1, 1, 0, 1, 0, 1, 1])

*  进行测试并计算准确率，首先取 k=1

# Now implement the function predict_labels and run the code below:
    # We use k = 1 (which is Nearest Neighbor).
    y_test_pred = classifier.predict_labels(dists, k=1)
    
    # Compute and print the fraction of correctly predicted examples
    num_correct = np.sum(y_test_pred == y_test)
    accuracy = float(num_correct) / num_test
    print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
    
    # 输出准确率
    Got 137 / 500 correct => accuracy: 0.274000

*  取 k=5

y_test_pred = classifier.predict_labels(dists, k=5)
    num_correct = np.sum(y_test_pred == y_test)
    accuracy = float(num_correct) / num_test
    print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
    
    # 输出准确率
    Got 139 / 500 correct => accuracy: 0.278000

*  可以看到k取5的效果会优于k取1，但这是随意取的，后续会使用交叉验证的方法来选择最优的超参数k，在下一篇博客进行记录吧
 *  接下来要将距离计算的效率提升一下，使用单层循环结构的计算方法，需要补全 compute\_distances\_one\_loop 方法，主要是利用了广播机制，减少了一层循环

def compute_distances_one_loop(self, X):
            """ Compute the distance between each test point in X and each training point in self.X_train using a single loop over the test data. Input / Output: Same as compute_distances_two_loops """
            num_test = X.shape[0]
            num_train = self.X_train.shape[0]
            dists = np.zeros((num_test, num_train))
            for i in range(num_test):
                #######################################################################
                # TODO: #
                # Compute the l2 distance between the ith test point and all training #
                # points, and store the result in dists[i, :]. #
                # Do not use np.linalg.norm(). #
                #######################################################################
                # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    			  # 利用broadcasting，一次性算出每一张图片与5000张图片的距离
                dists[i, :] = np.sqrt(np.sum(np.square(self.X_train - X[i, :]),axis=1))
    
                # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            return dists

*  还能继续优化吗？能！通过矩阵乘法和两次广播加法，可以不使用循环，就能完成计算任务

def compute_distances_no_loops(self, X):
            """ Compute the distance between each test point in X and each training point in self.X_train using no explicit loops. Input / Output: Same as compute_distances_two_loops """
            num_test = X.shape[0]
            num_train = self.X_train.shape[0]
            dists = np.zeros((num_test, num_train))
            #########################################################################
            # TODO: #
            # Compute the l2 distance between all test points and all training #
            # points without using any explicit loops, and store the result in #
            # dists. #
            # #
            # You should implement this function using only basic array operations; #
            # in particular you should not use functions from scipy, #
            # nor use np.linalg.norm(). #
            # #
            # HINT: Try to formulate the l2 distance using matrix multiplication #
            # and two broadcast sums. #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
            def compute_distances_no_loops(self, X):
            """ Compute the distance between each test point in X and each training point in self.X_train using no explicit loops. Input / Output: Same as compute_distances_two_loops """
            num_test = X.shape[0]
            num_train = self.X_train.shape[0]
            dists = np.zeros((num_test, num_train))
            #########################################################################
            # TODO: #
            # Compute the l2 distance between all test points and all training #
            # points without using any explicit loops, and store the result in #
            # dists. #
            # #
            # You should implement this function using only basic array operations; #
            # in particular you should not use functions from scipy, #
            # nor use np.linalg.norm(). #
            # #
            # HINT: Try to formulate the l2 distance using matrix multiplication #
            # and two broadcast sums. #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
            temp_2xy = np.dot(X,self.X_train.T) * (-2)
            temp_x2 = np.sum(np.square(X),axis=1,keepdims=True)
            temp_y2 = np.sum(np.square(self.X_train),axis=1)
            dists = temp_x2 + temp_2xy + temp_y2
            # 上述四行的作用，构造出了 x^2-2xy+y^2
            # 然后开根号即可
            dists = np.sqrt(dists)
    
            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            return dists
    
            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            return dists

*  这三个计算距离的函数所计算出的结果都是一样的，就不再赘述了，主要是比较一下他们的效率

# Let's compare how fast the implementations are
    def time_function(f, *args):
        """ Call a function f with args and return the time (in seconds) that it took to execute. """
        import time
        tic = time.time()
        f(*args)
        toc = time.time()
        return toc - tic
    
    two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
    print('Two loop version took %f seconds' % two_loop_time)
    
    one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
    print('One loop version took %f seconds' % one_loop_time)
    
    no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
    print('No loop version took %f seconds' % no_loop_time)

*  输出如下，可以很明显地看到效率差距

Two loop version took 47.337988 seconds
    One loop version took 45.795947 seconds
    No loop version took 0.334743 seconds

[iOwMHC.png]: https://upload.cc/i1/2019/05/23/iOwMHC.png
[gYHZEr.png]: https://upload.cc/i1/2019/05/23/gYHZEr.png
[ihXF8v.png]: https://upload.cc/i1/2019/05/23/ihXF8v.png