数字信号处理实验（二）：离散时间信号和线性时不变离散时间系统的频域分析

红太狼 2022-04-05 07:16 571阅读 0赞

目录

一、实验目的：

二、实验内容及要求：

  1. 离散时间信号的频域分析：

  2. 线性时不变离散时间系统的频域分析：

三、实验结果及问题回答：

  1. 离散时间信号的频域分析：

  2. 线性时不变离散时间系统的频域分析：

一、实验目的：

熟悉Mat lab中的信号处理工具箱及相关命令，掌握用Mat lab验证离散时间傅里叶变换相关性质的方法；掌握用Mat lab分析离散时间系统频域特性的方法并能绘制幅频特性和相频特性图。

二、实验内容及要求：

1. 离散时间信号的频域分析：

（1）修改程序P3.1，在范围内计算如下序列的离散时间傅里叶变换并绘制幅频特性和相频特性图。

（2）修改程序P3.2，D=8，验证离散时间傅里叶变换的时移特性并绘图。

（3）修改程序P3.3，，验证离散时间傅里叶变换的频移特性并绘图。

2. 线性时不变离散时间系统的频域分析：

（1）修改程序P3.1，计算并画出如下传输函数的频率响应，它是哪种类型的滤波器？

（2）修改程序P4.2，计算并画出一个长度为6的滑动平均滤波器的增益响应。

（3）用Mat lab画出如下滤波器的零极点图并分析稳定性。

三、实验结果及问题回答：

1. 离散时间信号的频域分析：

（1）实验结果：

  1. clf;
  3. w = 0:pi/511:pi;
  5. num = [0.7 -0.5 0.3 1];%系统频率响应的分子向量
  7. den = [1 0.3 -0.5 0.7];%系统频率响应的分母向量
  9. h = freqz(num, den, w);%求系统的频率响应
  11. subplot(2,1,1)
  13. plot(w/pi,real(h));grid
  15. title('Real part of H(e^{j\omega})')
  17. xlabel('\omega /\pi');
  19. ylabel('Amplitude');
  21. subplot(2,1,2)
  23. plot(w/pi,imag(h));grid
  25. title('Imaginary part of H(e^{j\omega})')
  27. xlabel('\omega /\pi');
  29. ylabel('Amplitude');
  31. pause
  33. subplot(2,1,1)
  35. plot(w/pi,abs(h));grid
  37. title('Magnitude Spectrum |H(e^{j\omega})|')
  39. xlabel('\omega /\pi');
  41. ylabel('Amplitude');
  43. subplot(2,1,2)
  45. plot(w/pi,angle(h));grid
  47. title('Phase Spectrum arg[H(e^{j\omega})]')
  49. xlabel('\omega /\pi');
  51. ylabel('Phase in radians');

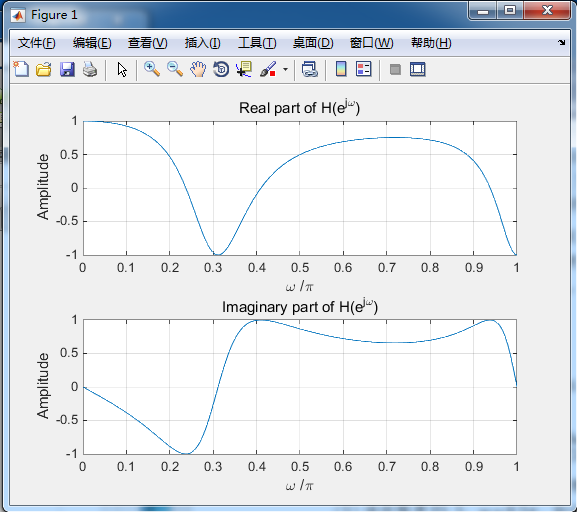
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70

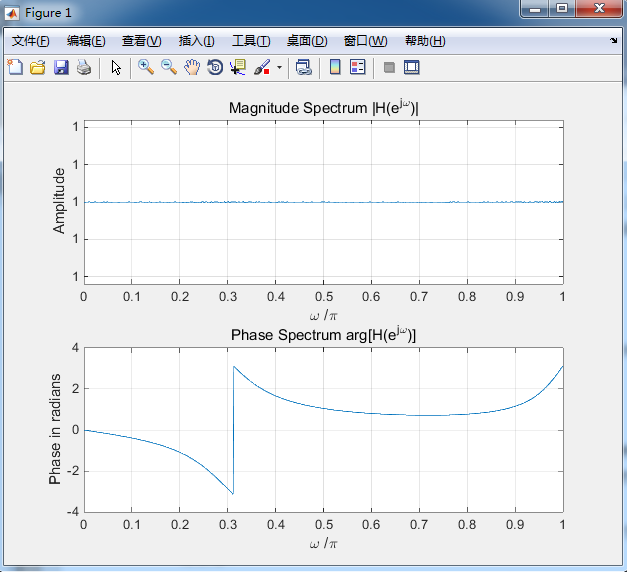
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 1

（2）实验结果：

  1. clf;
  3. w = -pi:2*pi/255:pi;
  5. wo = 0.4*pi;
  7. D = 8;%设定对原序列时移的大小
  9. num = [1 2 3 4 5 6 7 8 9];
  11. h1 = freqz(num, 1, w);%求原序列的频率响应
  13. h2 = freqz([zeros(1,D) num], 1, w);%在原序列前面加上一定数量的0，以达到对原序列进行时移的操作（时移不改变序列的频率响应，但是改变了相频特性）
  15. subplot(2,2,1)
  17. plot(w/pi,abs(h1));grid
  19. title('Magnitude Spectrum of Original Sequence')
  21. subplot(2,2,2)
  23. plot(w/pi,abs(h2));grid
  25. title('Magnitude Spectrum of Time-Shifted Sequence')
  27. subplot(2,2,3)
  29. plot(w/pi,angle(h1));grid
  31. title('Phase Spectrum of Original Sequence')
  33. subplot(2,2,4)
  35. plot(w/pi,angle(h2));grid
  37. title('Phase Spectrum of Time-Shifted Sequence')

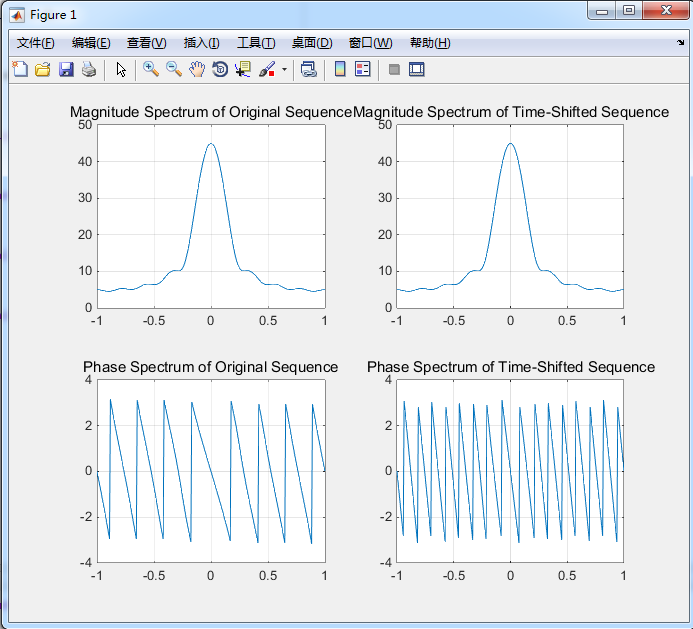
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 2

从图可以看出，原信号经过时移之后，系统函数的幅度响应没有发生变化，而相位谱发生了变化，相位谱的谱线比以前变得更密一些。

（3）实验结果：

  1. clf;
  3. w = -pi:2*pi/255:pi;
  5. wo = 0.2*pi;%设定对原序列频移的大小
  7. num1 = [1 3 5 7 9 11 13 15 17];%原序列
  9. L = length(num1);%求原序列的长度
  11. h1 = freqz(num1, 1, w);%求原序列的频率响应
  13. n = 0:L-1;
  15. num2 = exp(wo*i*n).*num1;%直接利用频移的性质公式来计算序列的频移
  17. h2 = freqz(num2, 1, w);%求频移后序列的频率响应（频移会改变序列的频率响应和相频特性）
  19. subplot(2,2,1)
  21. plot(w/pi,abs(h1));grid
  23. title('Magnitude Spectrum of Original Sequence')
  25. subplot(2,2,2)
  27. plot(w/pi,abs(h2));grid
  29. title('Magnitude Spectrum of Frequency-Shifted Sequence')
  31. subplot(2,2,3)
  33. plot(w/pi,angle(h1));grid
  35. title('Phase Spectrum of Original Sequence')
  37. subplot(2,2,4)
  39. plot(w/pi,angle(h2));grid
  41. title('Phase Spectrum of Frequency-Shifted Sequence')

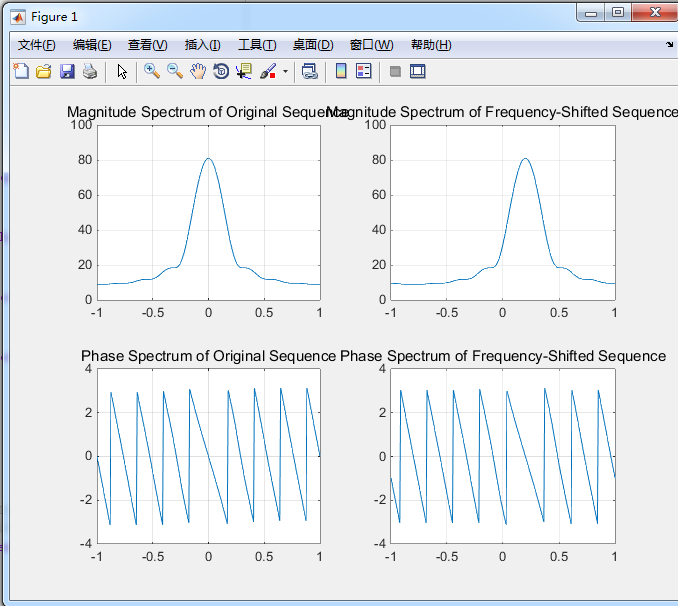
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 3

从图可以看出，原信号经过频移之后，系统函数的幅度响应和相位谱都发生了变化，并且幅度响应和相位谱都是仅仅发生了左右移动的变化。

2. 线性时不变离散时间系统的频域分析：

（1）实验结果：

  1. clf;
  3. w = 0:8*pi/511:pi;
  5. num = [0.15 0 -0.15];%传输函数的分子向量
  7. den = [1 -0.5 0.7];%传输函数的分母向量
  9. h = freqz(num, den, w);%求传输函数的频率响应
  11. subplot(2,1,1)
  13. plot(w/pi,real(h));grid
  15. title('Real part of H(e^{j\omega})')
  17. xlabel('\omega /\pi');
  19. ylabel('Amplitude');
  21. subplot(2,1,2)
  23. plot(w/pi,imag(h));grid
  25. title('Imaginary part of H(e^{j\omega})')
  27. xlabel('\omega /\pi');
  29. ylabel('Amplitude');
  31. pause
  33. subplot(2,1,1)
  35. plot(w/pi,abs(h));grid
  37. title('Magnitude Spectrum |H(e^{j\omega})|')
  39. xlabel('\omega /\pi');
  41. ylabel('Amplitude');
  43. subplot(2,1,2)
  45. plot(w/pi,angle(h));grid
  47. title('Phase Spectrum arg[H(e^{j\omega})]')
  49. xlabel('\omega /\pi');
  51. ylabel('Phase in radians');

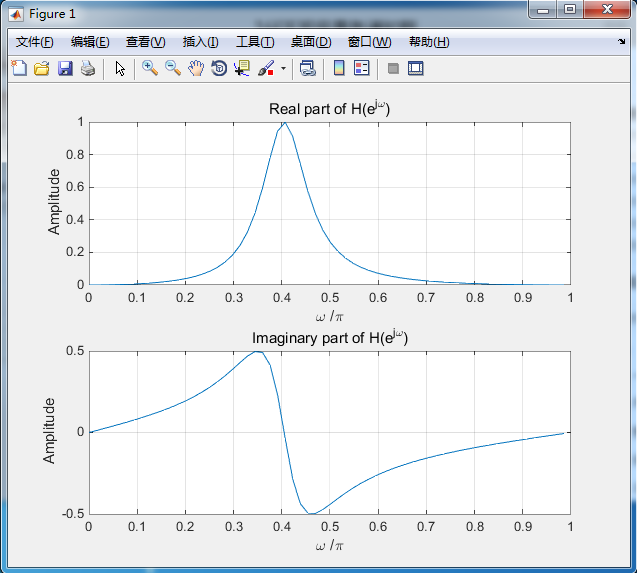
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 4

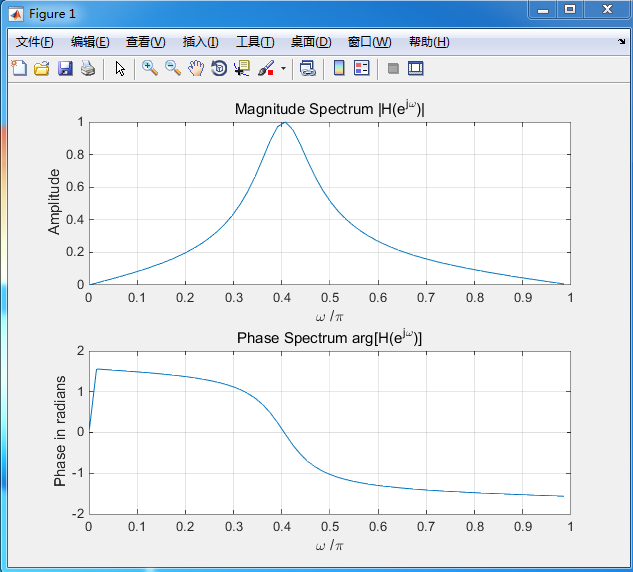
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 5

从频率响应图中可以看出，该滤波器是一个带通滤波器。

（2）实验结果：

  1. clf;
  3. M = 6;%设定滤波器的长度
  5. num = ones(1,M)/M;
  7. [g,w] = gain(num,1);%求增益函数
  9. plot(w/pi,g);grid
  11. axis([0 1 -50 0.5])
  13. xlabel('\omega /\pi');ylabel('Gain in dB');
  15. title(['M = ', num2str(M)])
  17. gain函数：
  19. function [g,w] = gain(num,den)
  21. w = 0:pi/255:pi;
  23. h = freqz(num,den,w);%求频率响应
  25. g = 20*log10(abs(h));%求频率响应h的增益响应

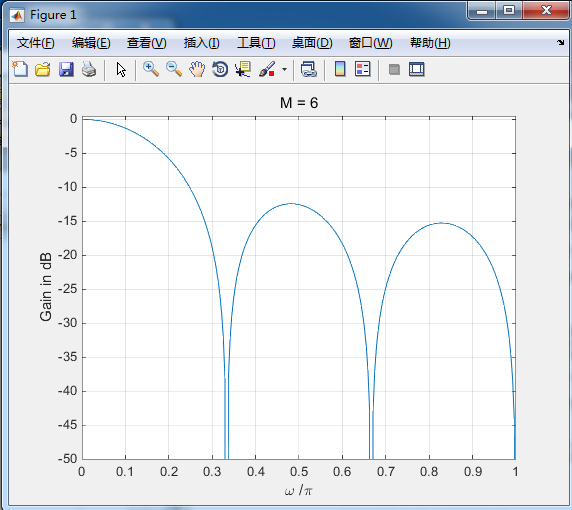
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 6

（3）实验结果：

  1. clf;
  3. num=[1];%设定函数的分子向量
  5. den = [1 -1.848 0.85];%设定函数的分母向量
  7. disp(roots(den));%输出零点
  9. zplane(num,den);%绘制系统函数的零极点图

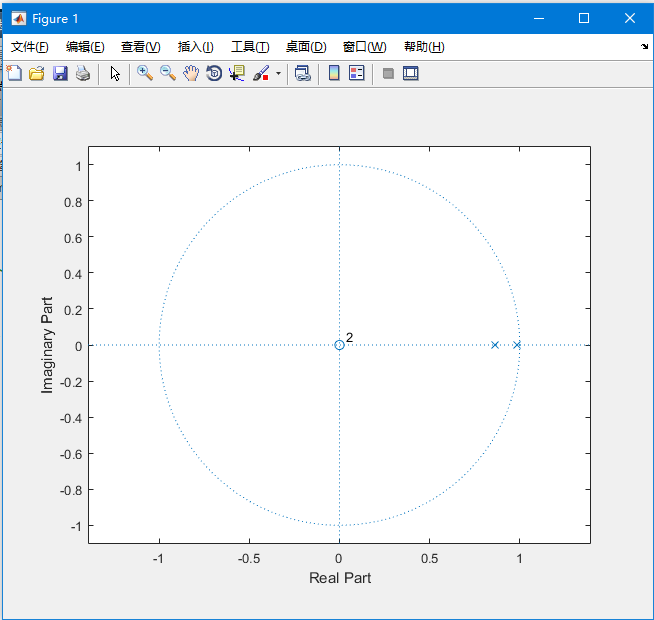
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1hpYW9tb19oYWE_size_16_color_FFFFFF_t_70 7

从零极点图可以看出来，该函数的2个极点均在单位圆内，即该系统是一个稳定的系统。

发表评论

表情：
评论列表 （有 0 条评论，571人围观）

还没有评论，来说两句吧...

相关阅读