基于堆的优先队列-蒲公英云

与传统队列（FIFO）不同，优先队列有两种特殊的操作：删除最大元素和插入元素。假设有一亿个不重复的数，现在从中删除最大数，如果没有优先队列的参与，可能先要遍历这一亿个数，然后标记最大的数，最后再删掉它。那如果还要继续删除第二大的数，那么还需遍历九千九百九十九万九千九百九十九个数，效率极低。可能你会想，对这一亿个数排序就行了。但是如果这时要插入一个数进来，那又得再遍历数组甚至再进行排序，效率也极低。这时，优先队列就能高效地实现上述操作了。

堆是一种优雅的数据结构，它通常是一个可以被看做一棵树的数组对象，堆中某个节点的值总是不大于或不小于其父节点的值。我们可以使用二叉堆来实现优先队列。二叉堆定义如下：二叉堆是一种特殊的堆，二叉堆是完全二元树（二叉树）或者是近似完全二元树（二叉树）。二叉堆有两种：最大堆和最小堆。最大堆：父节点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

由二叉树的性质可知，按层次从左到右为节点编号，若父节点的编号为k，则其左右子节点的编号分别为2k，2k+1。堆通常用数组来表示，且根节点的下标为1（便于计算）。以最大堆为例，如下图所示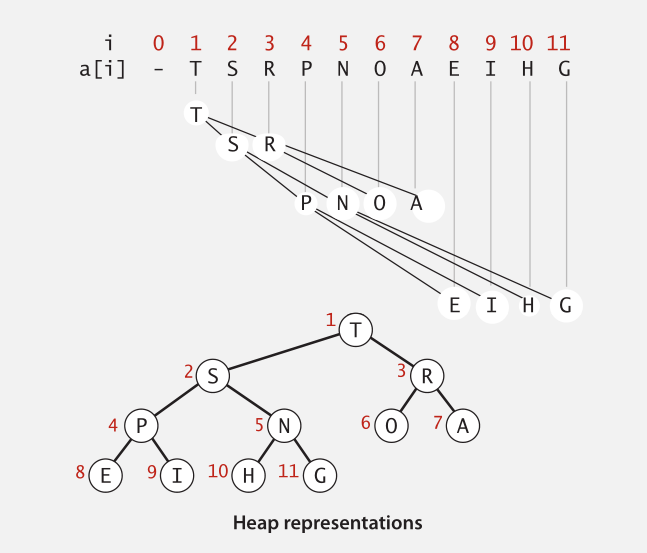： watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RYSDkyNA_size_16_color_FFFFFF_t_70

可以验证一下，上面这颗二叉树是一个很漂亮的最大堆。

二叉树的性质使得我们可以很容易地通过下标去操作堆：寻找k的父节点：[k/2]，左右子节点：[2k]，[2k+1]。

以最大堆为例，当堆的结构被破坏（某个父节点键值不大于子节点或子节点的键值大于了父节点时），我们就需要调整堆的结构来修复它。定义pq[]为基于堆的优先队列数组。

如果堆的有序状态因为某个节点大于其父节点而被打破时，我们就需要通过交换它和它的父节点来修复堆，这个操作称为“上浮（swim）”。通过循环不断交换当前节点与父节点直到其键值不大于父节点为止。

private void swim(Comparable[] pq, int k) {
        while (k > 1 && less(pq[k/2], pq[k])) {
            exch(pq, k/2, k);
            k /= 2;
        }
    }

上浮示例：

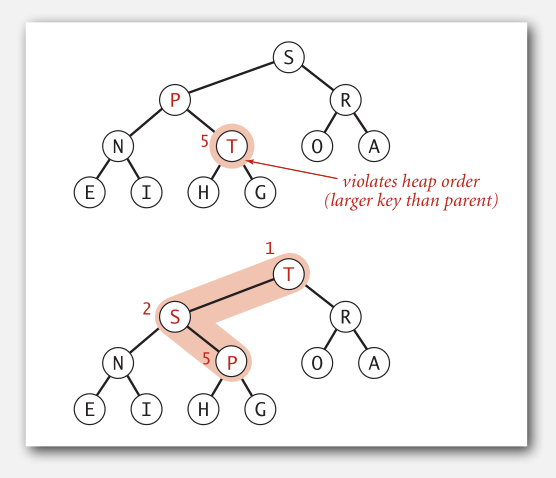
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RYSDkyNA_size_16_color_FFFFFF_t_70 1

相反，当某个节点的键值小于其子节点的键值时，我们要交换它和它的较大子节点来修复堆，直到对有序。这个操作形象化地称为“下沉（sink）”。

private void sink(Comparable[] pq, int k) {
        while (k*2 <= N) {
            int j = k*2;
            if (j < N && less(pq[j], pq[j+1]))
                j++;
            if (!less(pq[k], pq[j]))
                break;
            exch(pq, k, j);
            k = j;
        }
    }

下沉示例：

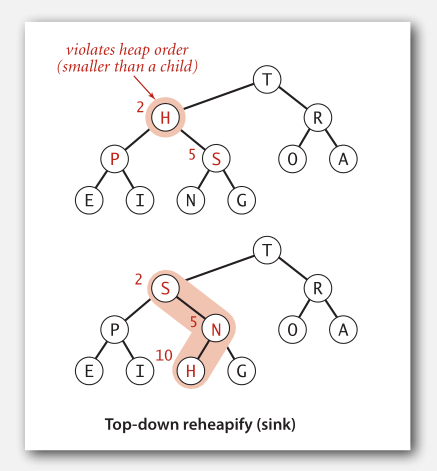
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RYSDkyNA_size_16_color_FFFFFF_t_70 2

当我们需要插入一个元素时，总是把它加到数组末尾（最后一个叶子节点），然后令其上浮到合适的位置。

public void insert(Key v) {
        pq[++N] = v;
        swim(pq, N);
    }

插入示例：

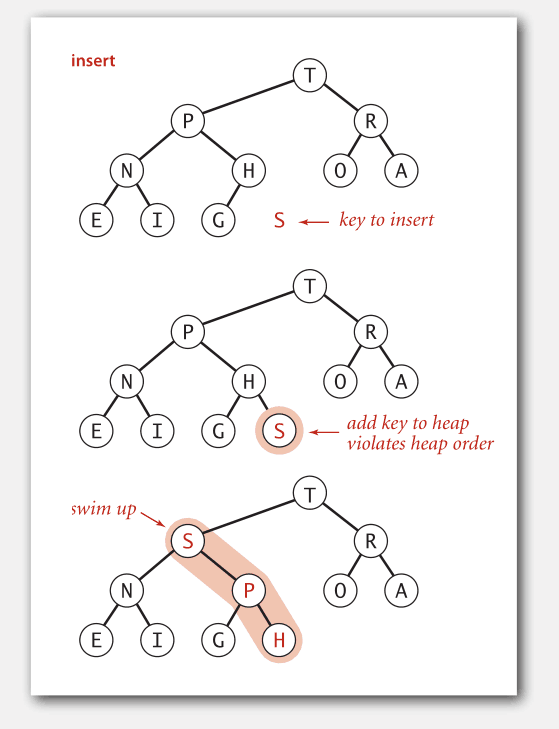
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RYSDkyNA_size_16_color_FFFFFF_t_70 3

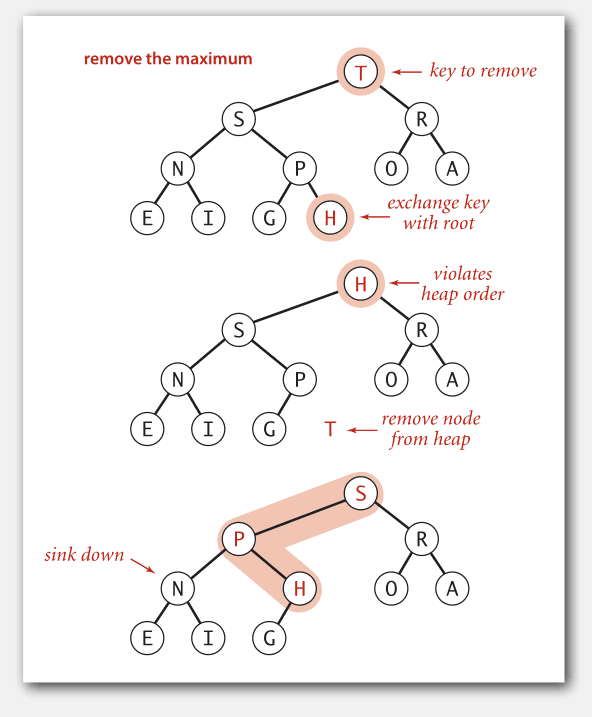
当我们要删除最大元素时，总是将它（根节点）与最后一个叶子节点交换，然后使新的根节点下沉到合适的位置，并将最后一个叶子节点置空。

public Key delMax() {
        Key max = pq[1];
        exch(pq, 1, N--);
        pq[N+1] = null;
        sink(pq, 1);
        return max;
    }

删除最大元素示例：

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RYSDkyNA_size_16_color_FFFFFF_t_70 4

算法分析：因为节点数为N的二叉树的高度小于等于lgN，所以对于二叉堆实现优先队列的插入和删除最大元素来说，用时仅和队列的大小成对数关系。

演示代码：

public class HeapPQ<Key extends Comparable<Key>> {
    private Key[] pq;
    private int N = 0;
    public HeapPQ(int maxN) {
        pq = (Key[]) new Comparable[maxN+1];
    }
    public boolean isEmpty() {
        return N == 0;
    }
    public int size() {
        return N;
    }
    public void insert(Key v) {
        pq[++N] = v;
        swim(pq, N);
    }
    public Key delMax() {
        Key max = pq[1];
        exch(pq, 1, N--);
        pq[N+1] = null;
        sink(pq, 1);
        return max;
    }
    private static boolean less(Comparable v, Comparable w){
        return v.compareTo(w)<0;
    }
    private static void exch(Comparable[] pq, int i, int j) {
        Comparable temp = pq[i];
        pq[i] = pq[j];
        pq[j] = temp;
    }
    private void swim(Comparable[] pq, int k) {
        while (k > 1 && less(pq[k/2], pq[k])) {
            exch(pq, k/2, k);
            k /= 2;
        }
    }
    private void sink(Comparable[] pq, int k) {
        while (k*2 <= N) {
            int j = k*2;
            if (j < N && less(pq[j], pq[j+1]))
                j++;
            if (!less(pq[k], pq[j]))
                break;
            exch(pq, k, j);
            k = j;
        }
    }
    public static void main(String[] args) {
        int N = 10;
        HeapPQ hp = new HeapPQ(N);
        for (int i = 0; i < N; i++) {
            hp.insert(N-i);
        }
        System.out.println("HeapPQ:");
        for (int i = 1; i <= N; i++) {
            System.out.print(hp.pq[i]+" ");
        }
        System.out.println("\n");
        for (int i = 0; i < N; i++) {
            System.out.println("delMax from hp.pq[]:"+hp.delMax());
            for (int j = 1; j <= hp.size(); j++) {
                System.out.print(hp.pq[j]+" ");
            }
            System.out.println("\n");
        }
    }
}

删除最大元素测试结果（插入操作可自行测试）：

HeapPQ:
10 9 8 7 6 5 4 3 2 1 
delMax from hp.pq[]:10
9 7 8 3 6 5 4 1 2 
delMax from hp.pq[]:9
8 7 5 3 6 2 4 1 
delMax from hp.pq[]:8
7 6 5 3 1 2 4 
delMax from hp.pq[]:7
6 4 5 3 1 2 
delMax from hp.pq[]:6
5 4 2 3 1 
delMax from hp.pq[]:5
4 3 2 1 
delMax from hp.pq[]:4
3 1 2 
delMax from hp.pq[]:3
2 1 
delMax from hp.pq[]:2
1 
delMax from hp.pq[]:1