根据先序和中序序列重建二叉树（打印二叉树的后序序列）

叁歲伎倆 2022-04-15 06:52 158阅读 0赞

### 1.重建条件 ###

我们知道，要重建二叉树，**必须得有中序序列**，有了中序，才可以划分出根结点的左子树和右子树。

而由先序和后序可以很容易确定根结点，因此，**先序和中序**或者**后序和中序**可以唯一确定二叉树。

此处运用递归的方法，仅以先序和中序序列为代表，给出重建二叉树的代码，供大家参考。

### 2.核心代码 ###

//根据先序和中序重建二叉树，pre和mid分别指向先序和中序序列，n为结点总数
    BiTree BuildTree(char *pre,char *mid,int n)
    {
    	if(n==0)
    		return error;
    	BiTree T=(BiTree)malloc(sizeof(BiNode));
    	if(!T)   exit(overflow);
            
            //T是根结点，pre[0]即先序第一个元素就是根结点的数据域
            T->data=pre[0]; 	
            
            int i;
    	//在中序序列中找出根结点的位置，记作i
            for(i=0;i<n;i++)
    	{
    		if(mid[i]==pre[0]) break;
    	}
    	
            //若中序序列中mid[i]是根结点，则左子树共有i个结点，在先序中从pre+1开始 
            T->lchild=BuildTree(pre+1,mid,i); 
            //右子树共有n-i-1个结点，在先序中从pre+i+1开始	
            T->rchild=BuildTree(pre+i+1,mid+i+1,n-i-1); 
    	
            return T;//返回根结点
    }

### 3.完整代码 ###

后序遍历上篇写过，在此不做赘述。

#include<stdio.h>
    #include<stdlib.h>
    //由先序序列和中序序列重建二叉树 
    
    #define ok 1
    #define error 0
    #define overflow -2
    
    typedef int Status;
    typedef char TElemType;
    
    typedef struct BiNode{
    	TElemType data;
    	struct BiNode *lchild,*rchild;
    }BiNode,*BiTree; 
    
    BiTree BuildTree(char *pre,char *mid,int n)
    {
    	if(n==0)
    		return error;
    	BiTree T=(BiTree)malloc(sizeof(BiNode));
    	if(!T)   exit(overflow);
    	T->data=pre[0];
    	
            int i;
    	for(i=0;i<n;i++)
    	{
    		if(mid[i]==pre[0]) break;
    	}
    	
            //若中序序列中mid[i]是根结点，则左子树共有i个结点，在先序中从pre+1开始 
            T->lchild=BuildTree(pre+1,mid,i); 
            //右子树共有n-i-1个结点，在先序中从pre+i+1开始	
            T->rchild=BuildTree(pre+i+1,mid+i+1,n-i-1); 
    	
            return T;
    }
    
    
    //后序遍历 
    Status PostOrderTraverse(BiTree T)
    {
    	if(T)
    	{
    		PostOrderTraverse(T->lchild );
    		PostOrderTraverse(T->rchild );
    		printf("%c",T->data);
    	}
    	return ok;
    }
    
    int main(){
    	char pre[20],mid[20];
    	int n;
    	printf("请输入结点总数：\n");
    	scanf("%d",&n);
    	
            printf("请依次输入先序序列和中序序列：\n");
    	scanf("%s",pre);
    	scanf("%s",mid);
    	
            BiTree T=BuildTree(pre,mid,n);
    	
            printf("后序序列为：\n");
    	PostOrderTraverse(T);
    	printf("\n");
    	system("pause");
    	return 0;
    }

### 4.运行截图  ###

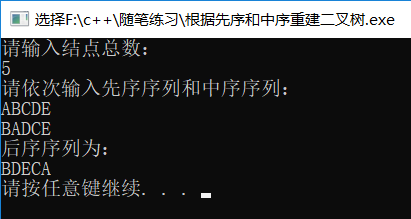
![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQyNDc1OTE0_size_16_color_FFFFFF_t_70][]

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQyNDc1OTE0_size_16_color_FFFFFF_t_70]: /images/20220415/dc77e271c149411aaa4930175d0d0b6b.png