JavaScript -- 几种常见的内部排序算法的JavaScript描述

深藏阁楼爱情的钟 2022-04-17 03:52 299阅读 0赞

对计算机中存储的数据执行的两种最常见操作是排序和检索，自从计算机产业伊始便是如此。这也意味着排序和检索在计算机科学中是被研究得最多的操作。

在面试当中，排序算法也是问的比较多的一方面。无论你是前端还是后台，学习算法知识，是IT工程师是必修课，苦行课。

我们要做探索者，不能只会用黑盒子（sort()函数），就像国家一直想做出国产芯片一样，自己明白原理是最好的。

提示：以下排序算法均按照从小到大排序。

1：冒泡排序

冒泡排序简单的说就是每一次循环就是将未排序的数组中最大的数移到数组尾。如何移动了？

每一次与相连的数比较，if (arr[i] > arr [i+1]) swap (arr[i],arr[i+1]);

  1. this.bubbleSort = function () {
  2.         for (let i = 0; i < this.length(); i++) {//N个数，循环n次
  3.             for (let j = 0; j < this.length() - 1 - i; j++) {
  4.                 if (this.array[j] > this.array[j+1]) this.swap(j,j+1);//将最大数移到尾部
  5.             }
  6.         }
  7.     };

时间复杂度O(n^2) 很慢。

2：选择排序

选择排序从数组的开头开始，将第一个元素和其他元素进行比较。检查完所有元素后，最小的元素会被放到数组的第一个位置，然后算法会从第二个位置继续。这个过程一直进行，当进行到数组的倒数第二个位置时，所有的数据便完成了排序。

  1. this.selectSort = function () {
  2.         for (let i = 0; i < this.length(); i++) {
  3.             for (let j = i + 1; j < this.length(); j++) {//注意前面0到i-1都是排好的，正在觉得i的位置
  4.                 if (this.array[i] > this.array[j]) this.swap(i,j);
  5.             }
  6.         }
  7.     };

时间复杂度O(n^2) 很慢。

3：插入排序

插入排序简单的说就是往已经排好序的数组里面插入下一个数，并使得新数组也是有序的。主要看程序。

  1. this.insertSort = function () {
  2.         let temp;
  3.         for (let i = 1; i < this.length(); i++) {//从1开始，往有序数组（其实只有array[0]这一个元素）添加其他数
  4.             if (this.array[i] < this.array[i-1]) {//添加数比它前一个小，安排它去合适的位置
  5.                 temp = this.array[i];//保存它的值
  6.                 this.array[i] = this.array[i-1];//你要让位给比你大的（因为此时前面的数组已经是排好的，它其实是最大值）
  7.                 let j;
  8.                 for (j = i - 2; this.array[j] > temp && j >= 0; j--) {//开始寻找一个比你小的的位置
  9.                     this.array[j+1] = this.array[j];
  10.                 }
  11.                 j = Math.max(0, j);//如果你最小，那么循环结束时j等于-1，所以你应该放在array[0]上
  12.                 this.array[j] = temp;
  13.             }
  14.         }
  16.     };

时间复杂度O(n^2) 很慢。

4：希尔排序

希尔排序又称缩小增量排序：先将整个待排序记录序列分割成为若干子序列分别进行插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次插入排序。

举个栗子

我们选择增量为5 3 1。

对于序列{12,2,16,30,28,10,16*,20,6,18}，增量为5时，我们排序的子序列为下标为1 6与2 7与3 8与4 9与5 10（以1开始）

即{12，10} {2，16*}{16，20}{30，6}{28，18}分别对这5个子序列进行排序为{10，12} {2，16*}{16，20}{6，30}{18，28}

则原序列变成{10,2,16,6,18,12,16*,20,30,28}

再选增量为3时:我们排序的子序列为1 4 7 10与2 5 8与3 6 9 依次把他们排序好后，原序列变成{6,2,12,10,18,16,16*,20,30,30,28}

我们发现大部分元素的位置关系已经都很对了，最后我们选择增量为1（注意最后一定要选增量为1，即进行直接插入排序）

原序列变成{2,6,10,12,16,16*,18,20,18,30}有序了！

我们都知道直接插入排序很多时间都浪费在查找和移动元素上面，不难发现经过前面俩趟希尔排序，我们的序列已经很有序了，换句话说就是离它应该待的位置很接近了，所以进行直接插入排序时，节省了很多时间！！！希尔排序优化点

还有一点：增量是随机选取的吗？很明显不是的，但是没有一个最优的增量选取，一般都是选取互质数，依次递减，最后选取增量为1.

  1. this.shellInsertSort = function (gap) {
  2.         let temp;
  3.         for (let i = 0; i < gap; i++) {//有gap的子序列
  4.             for (let j = i + gap; j < this.length(); j += gap) {//每一次增量是gap
  5.                 if (this.array[j] < this.array[j-gap]) {//后面代码和插入排序代码类似，不过增量是gap
  6.                     temp = this.array[j];
  7.                     this.array[j] = this.array[j-gap];
  8.                     let k;
  9.                     for (k = j - 2*gap; this.array[k] > temp && k >= i; k -= gap) {
  10.                         this.array[k+gap] = this.array[k];
  11.                     }
  12.                     k = Math.max(i, k);
  13.                     this.array[k] = temp;
  14.                 }
  15.             }
  16.         }
  17.     };
  18.     this.shellSort = function () {
  19.         const dlbt = [5,3,1];//增量
  20.         for (let i = 0; i < dlbt.length; i++) {//对每一个增量，进行插入排序
  21.             this.shellInsertSort(dlbt[i]);
  22.         }
  23.     };

希尔排序的时间复杂度是经过大量实验表明为O(n^(3/2))。算法不稳定，有时飞快，看你的增量选取，目前没有数学证明其时间复杂度。

5：归并排序

归并排序是高级排序算法，主要思想是分治，简单的说就是将大数组[left,right]分成[left,mid] 和[mid+1,right]（其中mid = Math.floor((left+right)/2);)分成俩个小数组,将小数组排好序，然后将俩个数组合并。

举个栗子

Center

具体看一下代码：

  1. this.merge = function (left, right) {
  2.         let temp = [].concat(this.array);
  3.         //因为我需要对this.array排序，所以我们复制一份
  4.         let mid =  Math.floor((left + right) / 2), i, j, pos = left;
  5.         //我们将[left,right]分成俩部分[left,mid]和[mid+1,right]
  6.         //然后定义俩个变量i,j分别取数，谁小就先取谁
  7.         for (i = left, j = mid + 1; i <= mid && j <= right;) {
  8.             if (temp[i] <= temp[j]) {//temp[i]小，取它，然后i++
  9.                 this.array[pos++] = temp[i++];//更换pos的位置的值
  10.             } else {
  11.                 this.array[pos++] = temp[j++];
  12.             }
  13.         }
  14.         //检查有没有其他值没有更换
  15.         while (i <= mid) this.array[pos++] = temp[i++];
  16.         while (j <= right) this.array[pos++] = temp[j++];
  19.     };
  20.     this.mSort = function (left,right) {
  21.         if (left >= right ) return ;//这个时候不应该在迭代了
  22.         let mid = Math.floor((left + right) / 2);//取中间
  23.         this.mSort(left, mid);//对左边继续划分
  24.         this.mSort(mid + 1, right);//对右边继续划分
  25.         this.merge(left, right);//对[left,right]这个部分进行排序
  26.     };
  27.     this.mergeSort = function () {//调用mSort函数，排序范围是[0,length-1]
  28.         this.mSort(0,this.length()-1);
  29.     };

时间复杂度O(nlogn)，空间复杂度O(n)（额外需要一个数组）

6：快速排序(快速排序是处理大数据集最快的排序算法之一)

快速排序通过一趟排序将待排记录分割成独立的俩部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这俩部分记录继续继续进行排序，已到达整个序列有序。

为了方便初始关键字（也可以称为轴）一般选取序列第一个元素。

简单的说，就是选取第一个数（轴），然后将原数组分成左右俩部分。左部分比轴要小，右部分比轴大，然后将俩部分继续这个操作。

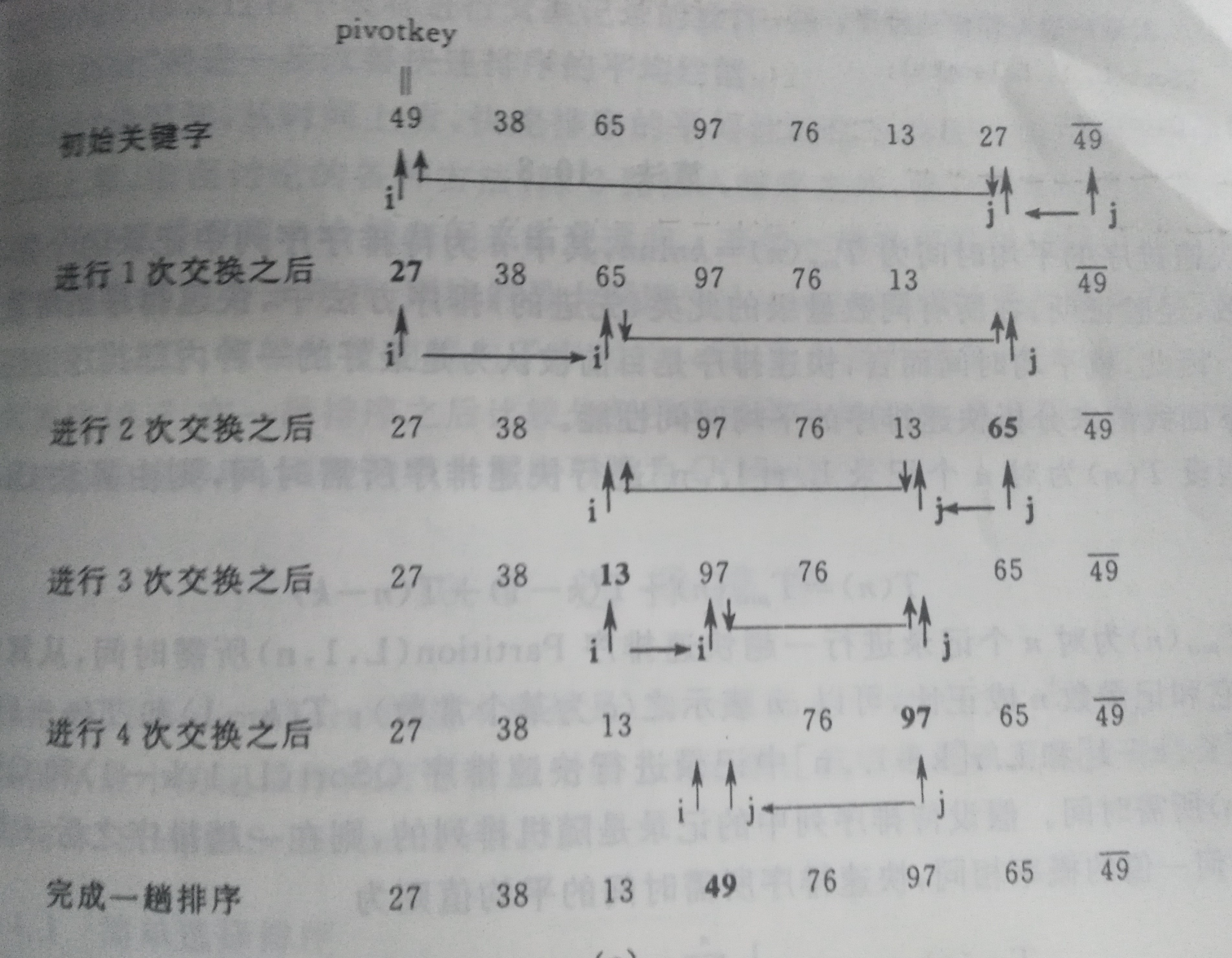
Center 1

49左边的比49小，49右边的比49大。

  1. this.partition = function(left,right) {
  2.         let mid = this.array[left];//轴
  3.         while (left < right) {//完成将[left,right]按照mid分成俩部分
  4.             while (right > left && this.array[right] >= mid) right--;//安排右边
  5.             this.array[left] = this.array[right];//找到比mid小的，这个地方为轴准备，然后这个地方的值放到上一个轴的位置
  6.             while (left < right && this.array[left] <= mid ) left++;//安排左边
  7.             this.array[right] = this.array[left];//找到比mid大的，这个地方为轴准备，然后这个地方的值放到上一个轴的位置
  8.         }
  9.         this.array[left] = mid;//将轴的值放到正确的位置
  10.         return left;   
  11.     };
  12.     this.qSort = function (left,right) {
  13.         if (left >= right) return ;
  14.         let mid =  this.partition(left,right);//将[left,right]完成一次快排，返回轴
  15.         this.qSort(left,mid-1);//将轴的左边继续这个操作
  16.         this.qSort(mid+1,right);//将轴的右边继续这个操作
  17.     };
  18.     this.quickSort = function () {//调用qSort函数，排序范围是[0,length-1]
  19.         this.qSort(0,this.length()-1);
  20.     };

时间复杂度O(nlogn) ，有一个最坏的时间复杂度O(n^2) (正好是逆序）

7：堆排序

堆排序：利用堆结构的一种树形选择排序，每次取堆顶，然后把剩下的n-1个元素维护成堆。反复操作得到一个有序序列。

n个元素的序列{k1,k2,k3,,,kn}当且仅当满足以下关系时，称为堆。

ki<=k2*i 或 ki>=k2*i

ki<=k2*i+1 ki>=k2*i+1

简单的来说，如果把堆看成树形结构的话，那么它是一棵完全二叉树且每个节点比他的俩个儿子都大（称为大顶堆）或者都小（称为小顶堆）。

以小顶堆为例：

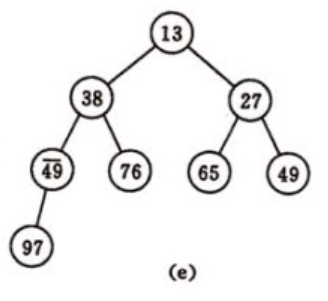
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3d1c3RfY3ls_size_16_color_FFFFFF_t_70

堆排序的难点在于，堆的建立和堆的维护。

因为我们的数组是从0开始的，所以左右儿子是2*i+1和2*i+2

堆排序的过程就不难理解了，因为根节点肯定是最大或者最小，每次把根节点移出，然后把剩下的元素维护成堆，重复操作。有点像冒泡排序对吧！但是它比冒泡排序要快很多。冒泡排序是将一个元素与其他的未排序的所有元素都进行比较了，很浪费时间，而堆排序不一样，因为堆的特殊性，例如大顶堆，节点总比儿子节点大，把根节点与最后一个元素交换后，我们只需要在儿子节点当中找比它大的最大儿子节点，找到了就替换，一直到儿子节点比小。log(n)的深度。

建堆操作：我们从序列lenth/2开始往前面调整，把每个节点i与它们的儿子节点2*i+1和2*i+2比较，如果儿子节点比它大就互换，然后重复操作。

  1. this.heapAdjust = function (pos, len) {//维护操作，维护第pos个节点，长度为len的数组，后面不用维护了
  2.         let temp = this.array[pos];//取值
  3.         let flag = true;//标记，是否找到了
  4.         for (let i = 2 * pos; i <= len ; i = i * 2) {
  5.             let x1 = ((this.array[i+1] == undefined || (i + 1) > len ) ? Number.MIN_VALUE : this.array[i+1]);
  6.             let x2 = ((this.array[i+2] == undefined || (i + 2) > len ) ? Number.MIN_VALUE : this.array[i+2]);
  7.             //左右儿子必须有意义且在len范围内，不然就是赋最小值（无意义的值）
  8.             let  maxValue, s;
  9.             if (x1 >= x2) {//找左右儿子的最大值
  10.                 s = i + 1,  maxValue = x1;
  11.             }
  12.             else {
  13.                 s = i + 2,  maxValue = x2;
  14.             }
  15.             if (temp > maxValue) {//如果比左右儿子都大，那么就应该放在这里
  16.                 this.array[pos] = temp;
  17.                 flag = false;//找到了
  18.                 break;
  19.             }
  20.             else {//有儿子比你大，那么就应该替换你的位置
  21.                 this.array[pos] = maxValue;
  22.                 i = s;
  23.                 pos = s;
  24.             }
  25.         }
  26.         if (flag) this.array[pos] = temp;
  27.     }
  28.     this.heapSort = function () {
  29.         for (let i = Math.floor((this.length() - 1) / 2); i >= 0; i--) {//建堆操作
  30.             this.heapAdjust(i,this.length()-1);
  31.         };
  33.         for (let i = this.length() - 1; i > 0; i--) {
  34.             this.swap(0,i);//将最大值放到堆尾
  35.             this.heapAdjust(0, i - 1 );//维护前面是堆，后面的已经是排好序的数组
  36.         }
  37.     }

时间复杂度O(nlogn)。

  1. let myArray = function () {
  2.     this.array = [];
  3.     this.length = function() {
  4.         return this.array.length;
  5.     };
  6.     this.add = function (data) {
  7.         this.array.push(data);
  8.     };
  9.     this.swap = function (x,y) {//交换函数
  10.         let temp = this.array[x];
  11.         this.array[x] = this.array[y];
  12.         this.array[y] = temp;
  13.     }; 
  14.     this.bubbleSort = function () {//冒泡排序
  15.         for (let i = 0; i < this.length(); i++) {//N个数，循环n次
  16.             for (let j = 0; j < this.length() - 1 - i; j++) {
  17.                 if (this.array[j] > this.array[j+1]) this.swap(j,j+1);//将最大数移到尾部
  18.             }
  19.         }
  20.     };
  21.     this.selectSort = function () {//选择排序
  22.         for (let i = 0; i < this.length(); i++) {
  23.             for (let j = i + 1; j < this.length(); j++) {//注意前面0到i-1都是排好的，正在觉得i的位置
  24.                 if (this.array[i] > this.array[j]) this.swap(i,j);
  25.             }
  26.         }
  27.     };
  28.     this.insertSort = function () {//插入排序
  29.         let temp;
  30.         for (let i = 1; i < this.length(); i++) {//从1开始，往有序数组（其实只有array[0]这一个元素）添加其他数
  31.             if (this.array[i] < this.array[i-1]) {//添加数比它前一个小，安排它去合适的位置
  32.                 temp = this.array[i];//保存它的值
  33.                 this.array[i] = this.array[i-1];//你要让位给比你大的（因为此时前面的数组已经是排好的，它其实是最大值）
  34.                 let j;
  35.                 for (j = i - 2; this.array[j] > temp && j >= 0; j--) {//开始寻找一个比你小的的位置
  36.                     this.array[j+1] = this.array[j];
  37.                 }
  38.                 j = Math.max(0, j);//如果你最小，那么循环结束时j等于-1，所以你应该放在array[0]上
  39.                 this.array[j] = temp;
  40.             }
  41.         }
  43.     };
  44.     this.shellInsertSort = function (gap) { 
  45.         let temp;
  46.         for (let i = 0; i < gap; i++) {//有gap的子序列
  47.             for (let j = i + gap; j < this.length(); j += gap) {//每一次增量是gap
  48.                 if (this.array[j] < this.array[j-gap]) {//后面代码和插入排序代码类似，不过增量是gap
  49.                     temp = this.array[j];
  50.                     this.array[j] = this.array[j-gap];
  51.                     let k;
  52.                     for (k = j - 2*gap; this.array[k] > temp && k >= i; k -= gap) {
  53.                         this.array[k+gap] = this.array[k];
  54.                     }
  55.                     k = Math.max(i, k);
  56.                     this.array[k] = temp;
  57.                 }
  58.             }
  59.         }
  60.     };
  61.     this.shellSort = function () {//希尔排序
  62.         const dlbt = [5,3,1];//增量
  63.         for (let i = 0; i < dlbt.length; i++) {//对每一个增量，进行插入排序
  64.             this.shellInsertSort(dlbt[i]);
  65.         }
  66.     };
  67.     this.merge = function (left, right) {
  68.         let temp = [].concat(this.array);
  69.         //因为我需要对this.array排序，所以我们复制一份
  70.         let mid =  Math.floor((left + right) / 2), i, j, pos = left;
  71.         //我们将[left,right]分成俩部分[left,mid]和[mid+1,right]
  72.         //然后定义俩个变量i,j分别取数，谁小就先取谁
  73.         for (i = left, j = mid + 1; i <= mid && j <= right;) {
  74.             if (temp[i] <= temp[j]) {//temp[i]小，取它，然后i++
  75.                 this.array[pos++] = temp[i++];//更换pos的位置的值
  76.             } else {
  77.                 this.array[pos++] = temp[j++];
  78.             }
  79.         }
  80.         //检查有没有其他值没有更换
  81.         while (i <= mid) this.array[pos++] = temp[i++];
  82.         while (j <= right) this.array[pos++] = temp[j++];
  84.     };
  85.     this.mSort = function (left,right) {
  86.         if (left >= right ) return ;//这个时候不应该在迭代了
  87.         let mid = Math.floor((left + right) / 2);//取中间
  88.         this.mSort(left, mid);//对左边继续划分
  89.         this.mSort(mid + 1, right);//对右边继续划分
  90.         this.merge(left, right);//对[left,right]这个部分进行排序
  91.     };
  92.     this.mergeSort = function () {//归并排序
  93.         this.mSort(0,this.length()-1);//调用mSort函数，排序范围是[0,length-1]
  94.     };
  95.     this.partition = function(left,right) {
  96.         let mid = this.array[left];//轴
  97.         while (left < right) {//完成将[left,right]按照mid分成俩部分
  98.             while (right > left && this.array[right] >= mid) right--;//安排右边
  99.             this.array[left] = this.array[right];//找到比mid小的，这个地方为轴准备，然后这个地方的值放到上一个轴的位置
  100.             while (left < right && this.array[left] <= mid ) left++;//安排左边
  101.             this.array[right] = this.array[left];//找到比mid大的，这个地方为轴准备，然后这个地方的值放到上一个轴的位置
  102.         }
  103.         this.array[left] = mid;//将轴的值放到正确的位置
  104.         return left;   
  105.     };
  106.     this.qSort = function (left,right) {
  107.         if (left >= right) return ;
  108.         let mid =  this.partition(left,right);//将[left,right]完成一次快排，返回轴
  109.         this.qSort(left,mid-1);//将轴的左边继续这个操作
  110.         this.qSort(mid+1,right);//将轴的右边继续这个操作
  111.     };
  112.     this.quickSort = function () { //快速排序
  113.         this.qSort(0,this.length()-1);//调用qSort函数，排序范围是[0,length-1]
  114.     };
  115.     this.heapAdjust = function (pos, len) {//维护操作，维护第pos个节点，长度为len的数组，后面不用维护了
  116.         let temp = this.array[pos];//取值
  117.         let flag = true;//标记，是否找到了
  118.         for (let i = 2 * pos; i <= len ; i = i * 2) {
  119.             let x1 = ((this.array[i+1] == undefined || (i + 1) > len ) ? Number.MIN_VALUE : this.array[i+1]);
  120.             let x2 = ((this.array[i+2] == undefined || (i + 2) > len ) ? Number.MIN_VALUE : this.array[i+2]);
  121.             //左右儿子必须有意义且在len范围内，不然就是赋最小值（无意义的值）
  122.             let  maxValue, s;
  123.             if (x1 >= x2) {//找左右儿子的最大值
  124.                 s = i + 1,  maxValue = x1;
  125.             }
  126.             else {
  127.                 s = i + 2,  maxValue = x2;
  128.             }
  129.             if (temp > maxValue) {//如果比左右儿子都大，那么就应该放在这里
  130.                 this.array[pos] = temp;
  131.                 flag = false;//找到了
  132.                 break;
  133.             }
  134.             else {//有儿子比你大，那么就应该替换你的位置
  135.                 this.array[pos] = maxValue;
  136.                 i = s;
  137.                 pos = s;
  138.             }
  139.         }
  140.         if (flag) this.array[pos] = temp;
  141.     }
  142.     this.heapSort = function () {//堆排序
  143.         for (let i = Math.floor((this.length() - 1) / 2); i >= 0; i--) {//建堆操作
  144.             this.heapAdjust(i,this.length()-1);
  145.         };
  147.         for (let i = this.length() - 1; i > 0; i--) {
  148.             this.swap(0,i);//将最大值放到堆尾
  149.             this.heapAdjust(0, i - 1 );//维护前面是堆，后面的已经是排好序的数组
  150.         }
  151.     }
  152.     this.show = function () {
  153.         for (let i = 0; i < this.length(); i++) {
  154.             console.log(this.array[i]);
  155.         }
  156.     };
  157. }

可以随机10个数试试。

  1. let app = new myArray();
  2. for (let i = 0; i < 10; i++) {
  3.     app.add(Math.floor(Math.random()*100));
  5. } 
  7. // app.heapSort(); //排序方法，任选
  8. app.show();

哈哈，介绍完了，如果你还不清楚可以留言，如果你还喜欢其他排序算法，欢迎留言。

发表评论

表情：
评论列表 （有 0 条评论，299人围观）

还没有评论，来说两句吧...

相关阅读

    相关 几种常见的内部排序

    排序是计算机程序设计中的一种重要操作，它的功能是将一个数据元素的任意序列，重新排列成一个按关键字有序的序列。 排序分为内部排序和外部排序。 随着计算机的内存不断扩大和查找算

    以你之姓@以你之姓@/ 0 赞/ 379 阅读