poj 3233 Matrix Power Series-蒲公英云

poj 3233 Matrix Power Series

题目链接：点我
Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1
Sample Output

1 2
2 3

这个题有两种转移矩阵
详细看图：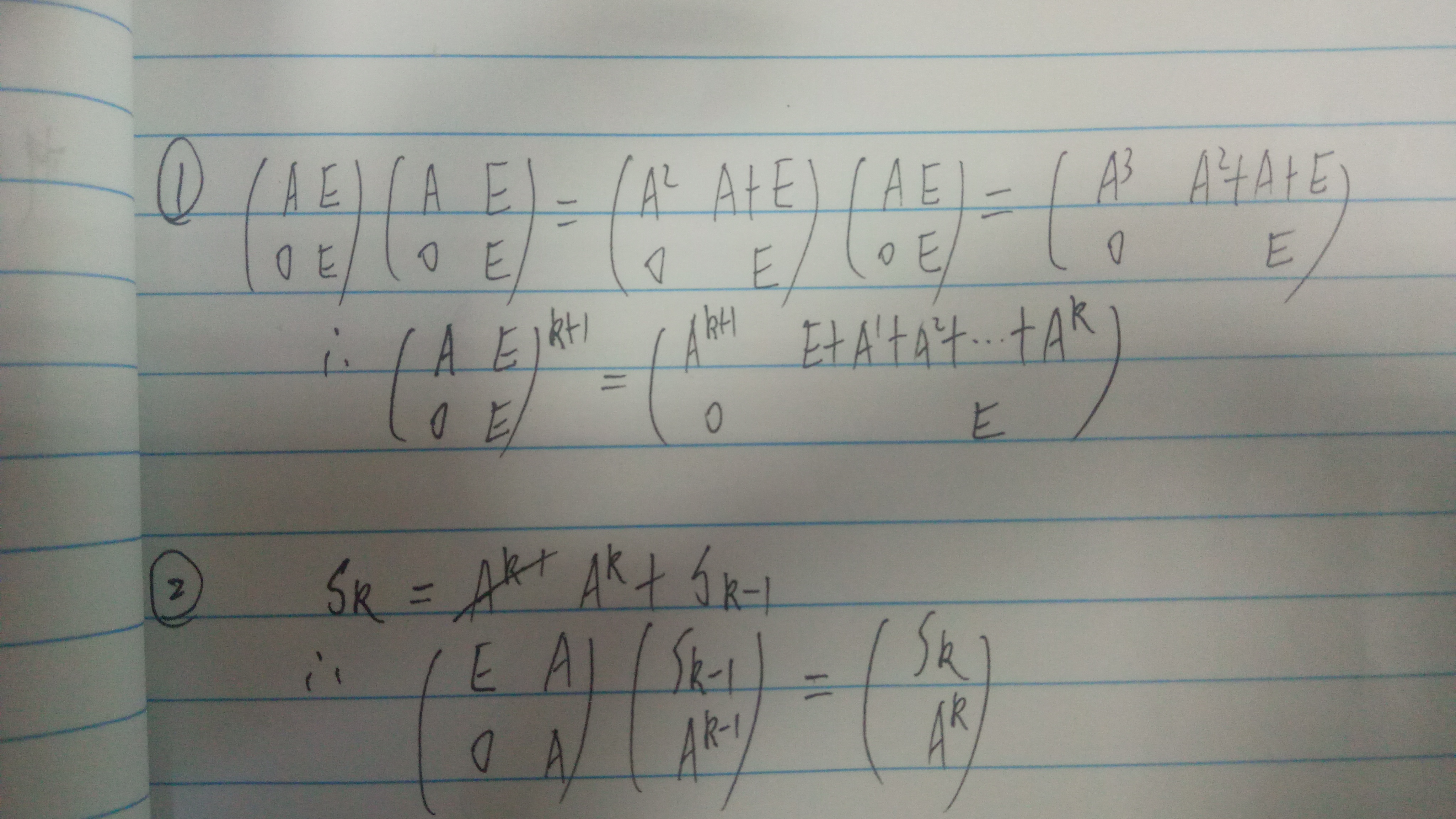
这里写图片描述

首先第一种方法，用到矩阵快速幂。

#include<stdio.h>
#include<string.h>
int mod,len,n;
const int ssize=66;
struct Matrix {
    int a[ssize][ssize];
    Matrix() {
        memset(a,0,sizeof(a));
    }
    void init() {
        for(int i=1; i<=len; i++)
            for(int j=1; j<=len; j++)
                a[i][j]=(i==j);
    }
    Matrix operator * (const Matrix &B)const {
        Matrix C;
        for(int i=1; i<=len; i++)
            for(int k=1; k<=len; k++)
                for(int j=1; j<=len; j++)
                    C.a[i][j]=(C.a[i][j]+1LL*a[i][k]*B.a[k][j])%mod;
        return C;
    }
    Matrix operator ^ (const int &t)const {
        Matrix A=(*this),res;
        res.init();
        int p=t;
        while(p) {
            if(p&1)res=res*A;
            A=A*A;
            p>>=1;
        }
        return res;
    }
};
int main()
{
    int i,j,k;
    while(scanf("%d%d%d",&n,&k,&mod)!=EOF)
    {   len=n*2;
         Matrix a,b;
        a.init();
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                scanf("%d",&a.a[i][j]);
        for(i=1;i<=n;i++)//右上部分
            for(j=n+1;j<=n*2;j++)
                if(i+n==j)
                    a.a[i][j]=1;
                else
                    a.a[i][j]=0;
        a=a^(k+1);
        for(i=1;i<=n;i++)//减去单位矩阵
            for(j=n+1;j<=len;j++)
            {
                if(i+n==j)
                    a.a[i][j]--;
                while(a.a[i][j]<0)//为了防止溢出
                    a.a[i][j]+=mod;
            }
        for(i=1;i<=n;i++)
        {
            for(j=n+1;j<len;j++)
                printf("%d ",a.a[i][j]);
            printf("%d\n",a.a[i][len]);
        }
    }
    return 0;
}

接下来第二种，用到自己的矩阵快速幂板子会超时
改了下转移矩阵，过了，700ms，说明这个转移矩阵是没问题的，
没想到结构体重载运算符竟然会这么慢

#include<stdio.h>
#include<string.h>
struct node {
    int p[65][65];
};
int mod,len;
struct node suan(struct node a,struct node b) { //矩阵a乘以矩阵b
    int i,j,k;
    struct node c;
    for(i=1; i<=len; i++) {
        for(j=1; j<=len; j++) {
            c.p[i][j]=0;
            for(k=1; k<=len; k++)
                c.p[i][j]=(a.p[i][k]*b.p[k][j]+c.p[i][j])%mod;
        }
    }
    return c;
}
struct node haha(struct node a,struct node b,int n){
    while(n) { //矩阵的快速幂
        if(n&1)
            b=suan(b,a);
        n>>=1;
        a=suan(a,a);
    }
    return b;
}
int main(){
    int i,j,n,k;
    struct node a,b,origin;
    while(scanf("%d%d%d",&n,&k,&mod)!=EOF) {
        len=n*2;
        for(i=1;i<=n;i++){
            for(j=1;j<=n;j++){
                a.p[i][j]=(i==j);
            }
        }
        for(i=1; i<=n; i++) { 
            for(j=n+1; j<=(n<<1); j++) {
                scanf("%d",&a.p[i][j]);
                a.p[i+n][j]=a.p[i][j];
                b.p[i][j-n]=a.p[i][j];
                b.p[i+n][j-n]=b.p[i][j-n];
            }
        }
        for(i=1; i<=n*2; i++) //把b变成单位矩阵
            for(j=1; j<=n*2; j++)
                 origin.p[i][j]=(i==j);
        a=haha(a,origin,k-1);
        b=suan(a,b);
        for(i=1;i<=n;i++){
            for(j=1;j<=n;j++){
                printf("%d ",b.p[i][j]);
            }
            printf("\n");
        }
    }
    return 0;
}