580-希尔排序算法的思想和性能分析

深藏阁楼爱情的钟 2022-09-12 00:55 142阅读 0赞

## 希尔排序算法的思想 ##

**希尔排序可以认为是插入排序的一个优化，升级。**  
如果数据序列从大的方向，从全局看，已经是趋于有序的，那么插入排序是所有排序算法中效率最高的。  
**希尔排序就是从插入排序的这句中总结优化的，它以自己最大的能力在全局中不断地把数据调整成趋于有序的，这样使得插入排序效率就越来越高。**

**插入排序**是按顺序从左到右，依次定位到元素，然后在前面已排序的序列中找到合适的位置插入。也就是说，随着插入排序的进行，只是前面那部分是有序的，从整体上表现出来，并不是越排越有序。  
**而希尔排序对插入排序的优化是，让全局数据序列越来越有序，尽最快的速度先变成趋于有序的序列，然后统一用插入排序进行处理。**

**希尔排序：对数据进行分组插入排序。**  
![在这里插入图片描述][0d0f32526a79427a8d9bc05d4d70faff.png]  
**我们进行第一次分组处理**  
![在这里插入图片描述][87857df1feb34f0395810741735cbd19.png]  
**每隔5个元素，把它们分到1个组里面。**  
25-87为一组， 进行插入排序。  
40-41为一组，进行插入排序。  
25-3为一组，进行插入排序。  
9-40为一组，进行插入排序。  
32-31为一组，进行插入排序。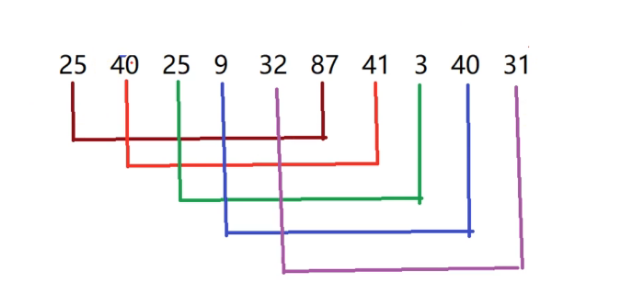  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16]  
**总共10个元素，每间隔5个位置的元素是一个组的，所以一组有2个元素，总共分为5组。**  
**这5组遍布了整个序列的前前后后。每一个组内进行插入排序。就是从全局尽快的把元素调整成趋于有序的。**

25和87是一组的，已经是有序的，40和41是一组的，已经是有序的。  
25和3是一组的，但是不是有序的，3和25进行交换，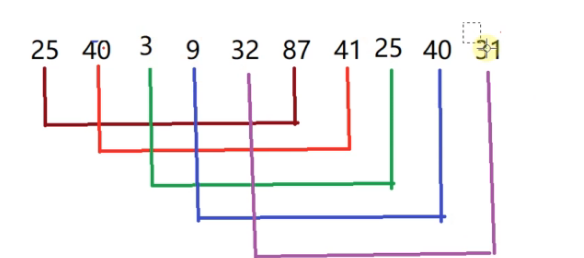  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 1]  
9和40是一组的，已经是有序的，不用进行交换  
32和31是一组的，但是不是有序的，我们把32和31交换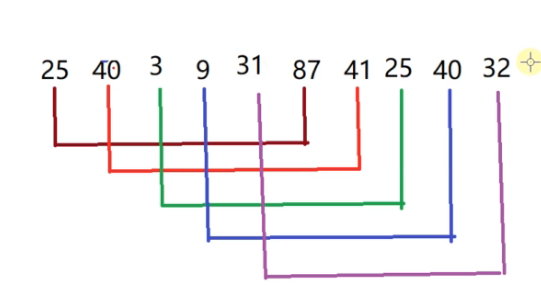  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 2]  
**从全局来看，数据已经趋于有序的了**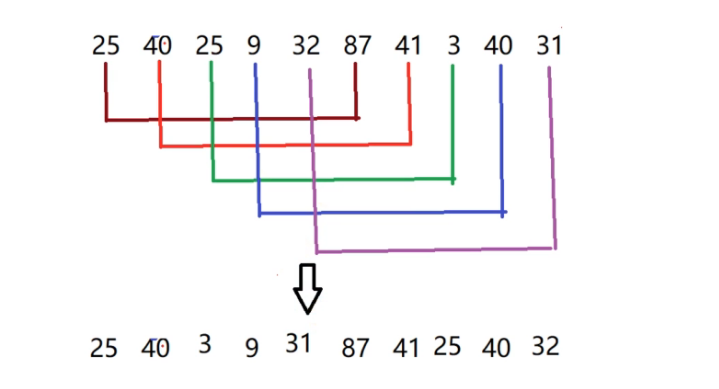  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 3]  
**然后进行第二次分组，gap继续缩小**  
每间隔2个位置的元素算是一个组 ，所以总共有2个组，1个组有5个元素，在同一组内进行插入排序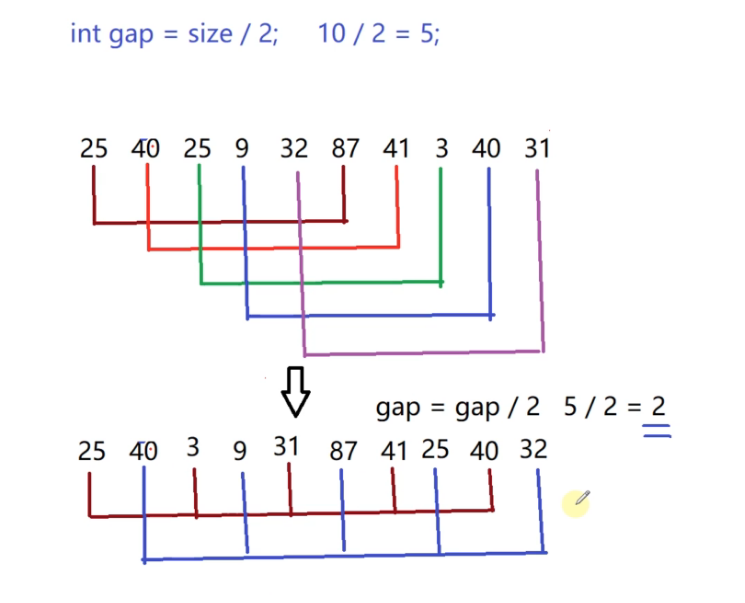  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 4]  
**25，3,31,41,40是一组的，但是不是有序的，进行插入排序。**  
![在这里插入图片描述][7d2cb75e3ce1404eb94cd19efd514631.png]  
**40,9，87,25,32是一组的，进行插入排序**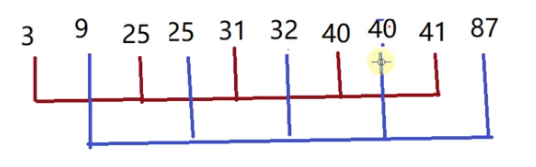  
![在这里插入图片描述][a07166b2466446fb9d776d67a85fce24.png]  
第二次分组，进行插入排序，已完成，整体更加趋于有序了。

**我们进行第三次分组处理**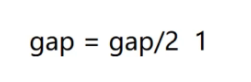  
![在这里插入图片描述][9a5a01d915c046bca97867e40de14e46.png]

这次就是每间隔1个位置的元素是一组，相当于是整个序列是一组的，进行插入排序。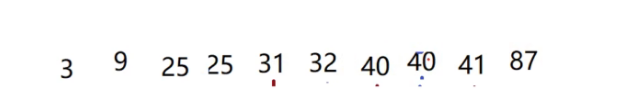  
![在这里插入图片描述][4abc385ec0aa4e838f5edcff798c79db.png]  
**处理完毕**  
**这一次处理完之后**  
gap=gap/2=1/2=0  
**希尔排序结束！**  
**注意**：对半分组不是一定要除以2的，除以3也可以，除以4也可以，我们要在实际情况中，根据实际的数据量进行分组的调整，测试一下性能是否达到最好的。

## 希尔排序算法的代码实现 ##

//希尔排序
    void ShellSort(int arr[], int size)
    {
        
    	for (int gap = size / 2; gap > 0; gap /= 2)//100W 19 1000W 24
    	{
        
    		for (int i = gap; i < size; i++)//O(n)i++:所有组都是要处理的 
    		{
        
    			int val = arr[i]; 
    			int j = i - gap;
    			for (; j >= 0; j-=gap)//O(n) 
    			{
        
    				if (arr[j] <= val)
    				{
        
    					break;
    				}
    				arr[j + gap] = arr[j];
    			}
    			arr[j + gap] = val;
    		}
    	}
    }

## 希尔排序算法的性能分析 ##

**最坏的时间复杂度：**  
O(n^2)  
**最外层的for循环相当于是二分搜索的概念，对于数据量的增长，这个for循环不用关注其性能的损耗了**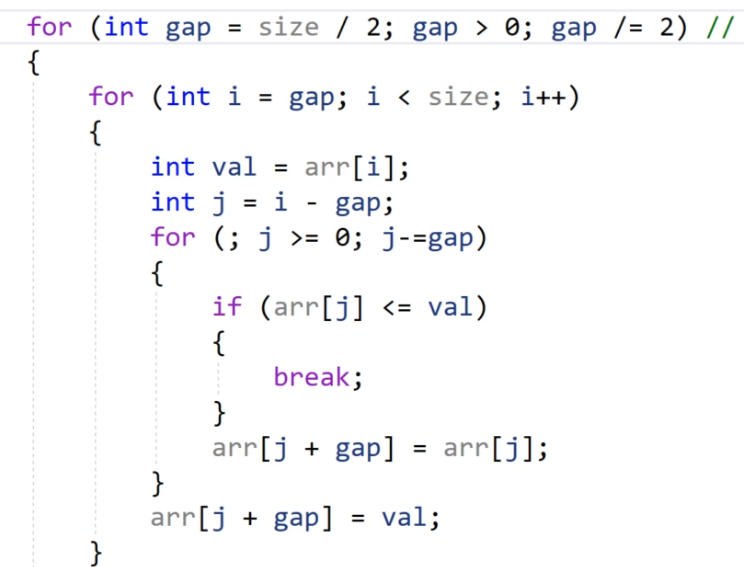  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 5]  
**最好的时间复杂度：O(n)  
相当于数据序列本身就是有序的，遍历了1遍而已**

**空间复杂度:O(1)**  
没有占用额外的空间，随着数据量的增长，我们在栈上申请的变量不会增多，空间的占用就是这两个变量

**不稳定：**  
因为它可能会把值相同的元素放在不同的组里面，然后就有可能发生相同元素的相对位置的变化。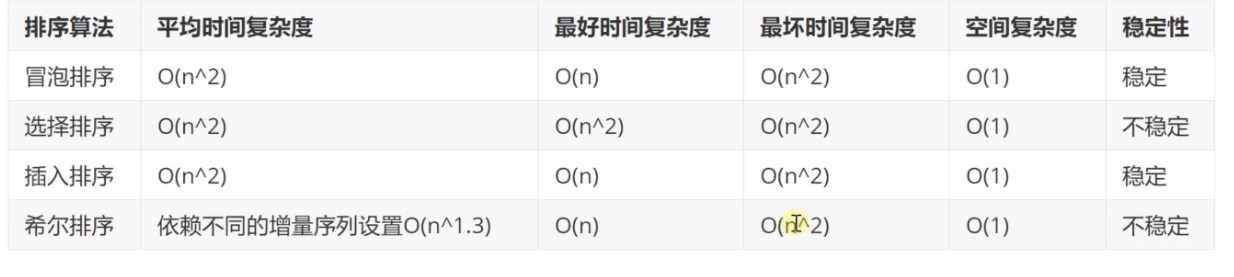  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 6]  
![在这里插入图片描述][cdb27355884241f0bfcad91705579a0b.png]  
**有时候我们要把快速排序和插入排序结合起来**

[0d0f32526a79427a8d9bc05d4d70faff.png]: /images/20220828/c31fdf30effd460689dbe31ad9a04f31.png
[87857df1feb34f0395810741735cbd19.png]: /images/20220828/5954954e75c54c48b76bb8e89a0be9da.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16]: /images/20220828/1d25e7b809394f06b0a535873f3ec603.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 1]: /images/20220828/2b901887af9e434f8c61f3df35665140.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 2]: /images/20220828/ff1e876d31db472b8755657eb8a67d5e.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 3]: /images/20220828/c82765ee8a7542bcb4278c453aa9b776.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 4]: /images/20220828/5caed6d9c9d845cd9d3d3c10b1296f6a.png
[7d2cb75e3ce1404eb94cd19efd514631.png]: /images/20220828/6494a5172bee4e0a890962118384c9d1.png
[a07166b2466446fb9d776d67a85fce24.png]: /images/20220828/65174d6cefa8494e8050e2587bcd99f5.png
[9a5a01d915c046bca97867e40de14e46.png]: /images/20220828/03e9414201414306a50b98c35cef9b9e.png
[4abc385ec0aa4e838f5edcff798c79db.png]: /images/20220828/5d35d260f7d44b00a09596fd9972df5c.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 5]: /images/20220828/9296ac9b69a544bab415a0f60cbc38fb.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBALeael-azveWuhw_size_20_color_FFFFFF_t_70_g_se_x_16 6]: /images/20220828/fb3043bb9de6450e8ef21b2a9e391f42.png
[cdb27355884241f0bfcad91705579a0b.png]: /images/20220828/372aca793dfb4fa490b50345b030a6e2.png