Java数据结构：归并排序/Merge sort（第三周）

ゞ浴缸里的玫瑰 2022-05-15 05:36 161阅读 0赞

题目来源：大工慕课 [链接][Link 1]  
作者：Caleb Sung

# 基本思想 #

**归并排序**（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的**分治**（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后**递归**求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即**分而治之**)。  
![这里写图片描述][70]  
可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

# 实现步骤 #

我们来看看治阶段。我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将\[4,5,7,8\]和\[1,2,3,6\]两个已经有序的子序列，合并为最终序列\[1,2,3,4,5,6,7,8\]，来看下实现步骤。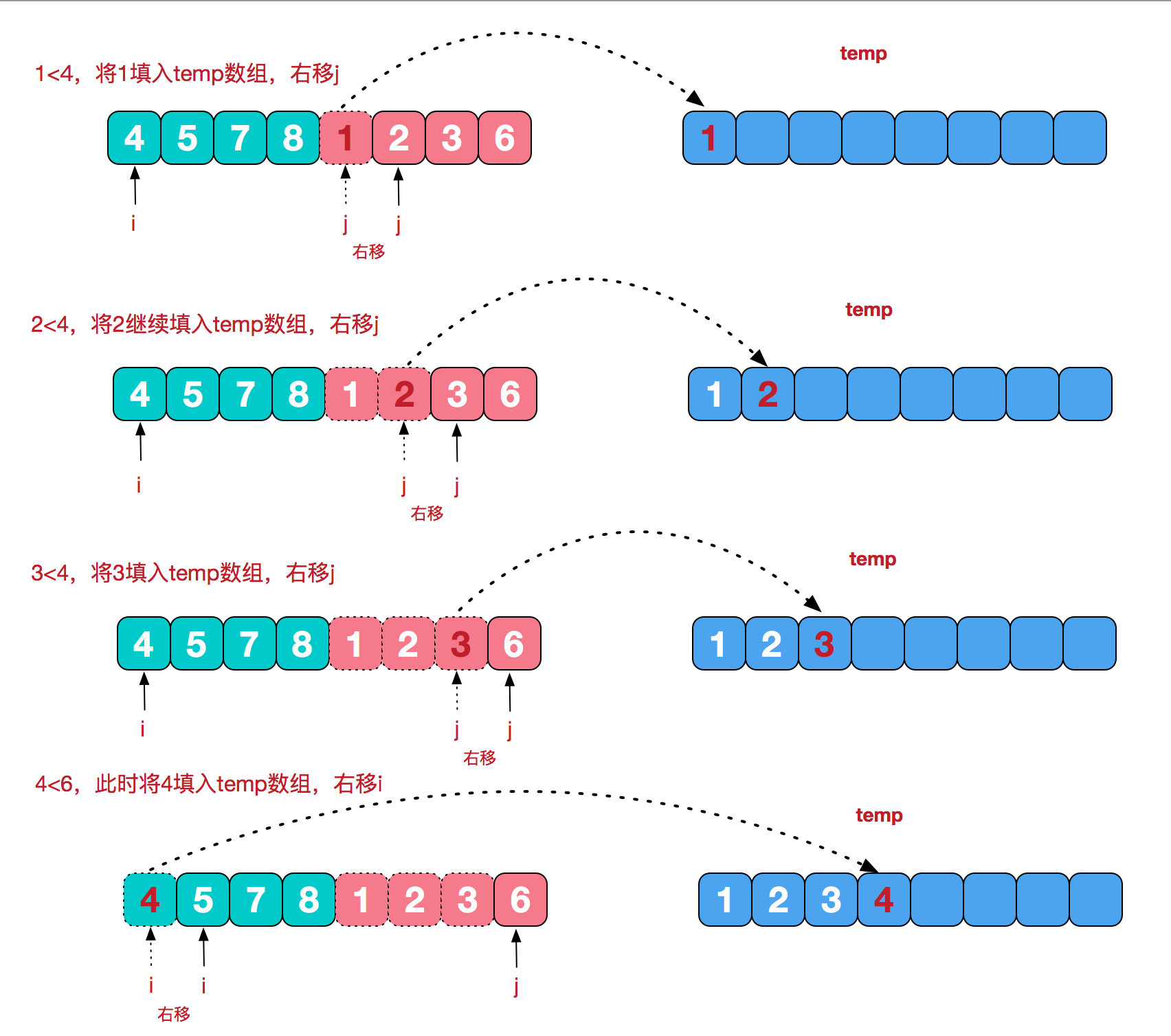  
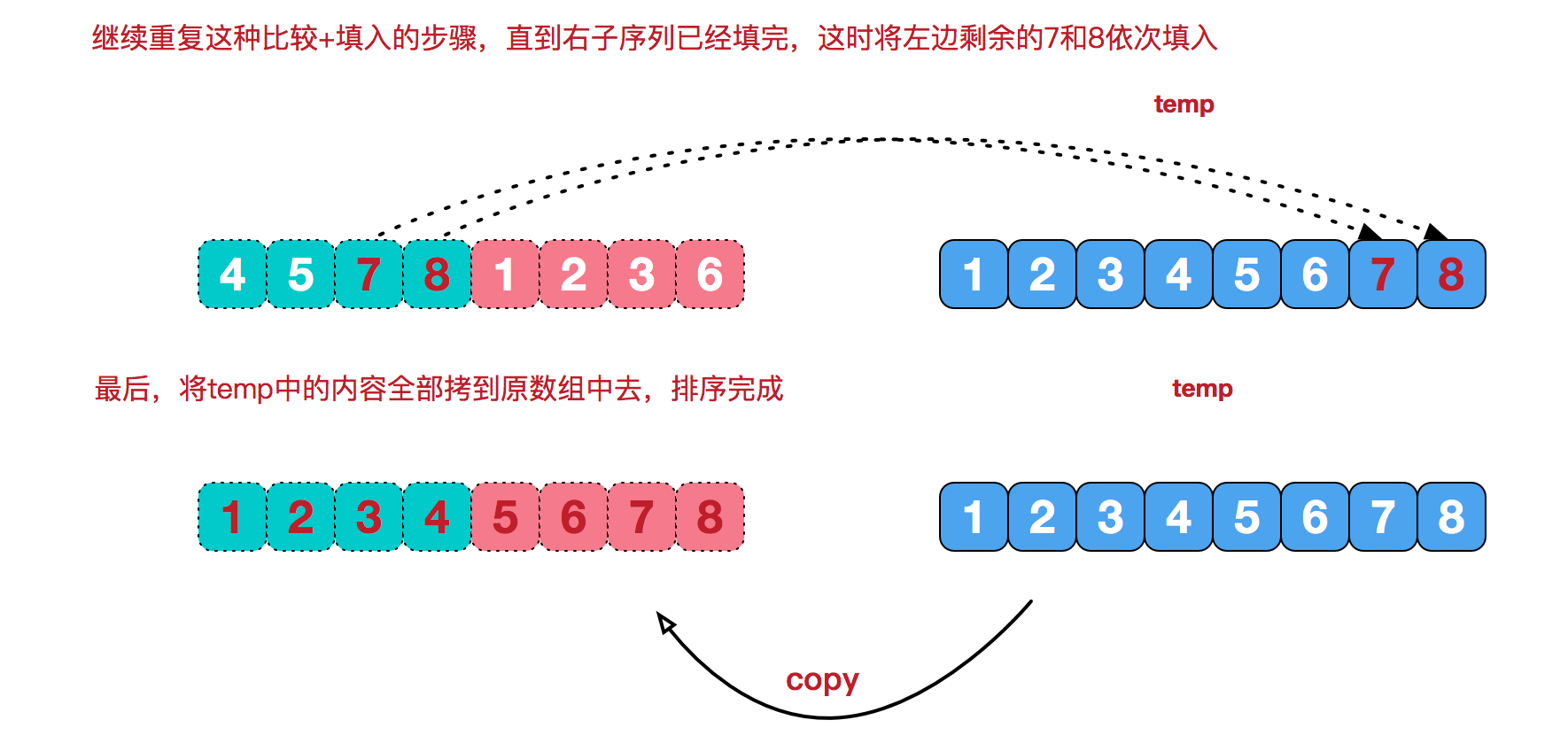
![这里写图片描述][70 1]  
![这里写图片描述][70 2]

--------------------

# 参考代码 #

## merge\_sort() ##

void merge_sort(int[] array, int p ,int r) {
        if(p < r) {
            int q = (p + r) / 2;
            merge_sort(array , p ,q);
            merge_sort(array , q+1 ,r);
            merge(array , p ,q , r);
        }
    }

# merge() #

void merge(int[] array , int p , int q ,int r) {
            int n1 = q-p+2;
            int n2 = r-q+1;
            int[] L = new int[n1];
            int[] R = new int[n2];
            for(int i = 0;i < n1-1; i++)
                L[i] = array[p + i];
            for(int j = 0 ; j < n2-1; j++)
                R[j] = array[q + j + 1];
            L[n1-1] = Integer.MAX_VALUE;
            R[n2-1] = Integer.MAX_VALUE;
            for(int k = p , i = 0 , j = 0; k <= r ;k++) {
                if(L[i] <= R[j]) {
                    array[k] = L[i];
                    i++;
                }
                else {
                    array[k] = R[j];
                    j++;
                }
            }
    
        }

# 主函数与测试用例 #

这里的测试用例需要手动输入若干个数字。并使用空格键隔开：

public static void main(String[] args) {
            int[] array = new int[8];
            Scanner in = new Scanner(System.in);
            for(int i = 0; i< array.length; i++)
                array[i] = in.nextInt();
            Homework_ds3 mergeSort = new Homework_ds3();
            mergeSort.merge_sort(array, 0, 7);
            for(int i : array)
                System.out.println(i);
        }

--------------------

# 归并排序算法的时间复杂度和稳定性 #

归并排序是**稳定排**序，它也是一种十分**高效的排序**，能利用**完全二叉树**特性的排序一般性能都不会太差。**Java**中`Arrays.sort()`采用了一种名为**TimSort**的排序算法，就是归并排序的优化版本。

## 归并排序时间复杂度 ##

归并排序的时间复杂度是O(N\*lgN)。  
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？  
归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的**时间复杂度是O(N\*lgN)**。

## 归并排序稳定性 ##

归并排序是稳定的算法，它满足稳定算法的定义。  
算法稳定性：假设在数列中存在a\[i\]=a\[j\]，若在排序之前，a\[i\]在a\[j\]前面；并且排序之后，a\[i\]仍然在a\[j\]前面。则**这个排序算法是稳定的**！

[Link 1]: https://mooc.dlut.edu.cn/
[70]: /images/20220515/b3c9a7b6fca74d4c8d80d5dc5f67e807.png
[70 1]: /images/20220515/e4da88f11124497d84ae567baef435a2.png
[70 2]: /images/20220515/6366bf6d81de4de0b9609bfe47aa7d17.png