排序——归并排序(Merge Sort)及应用
归并排序:是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
时间复杂度:O(nlgn)
空间复杂度:O(n)(用于存储有序子序列合并后有序序列)
稳定性:归并排序是稳定的排序
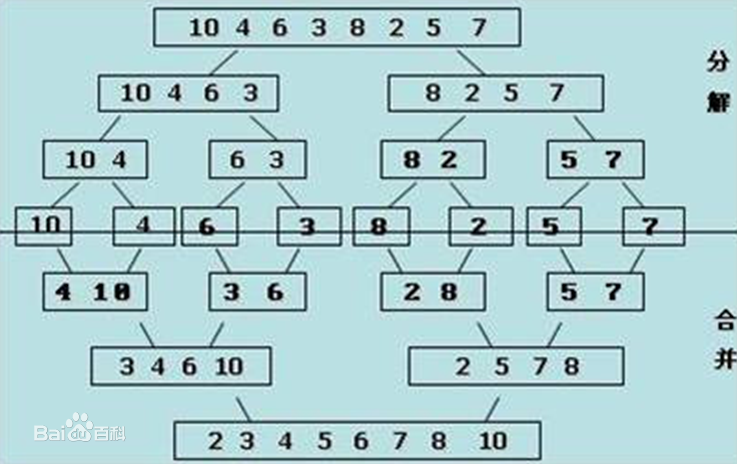
递归方法示意图(图来源网上)
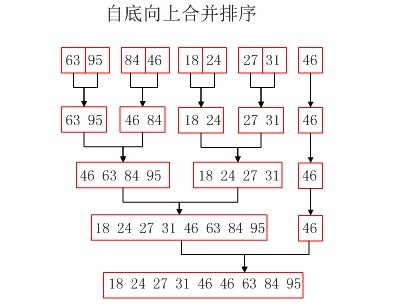
非递归方法示意图(图来源网上)
实例:
<pre name="code" class="cpp">//归并排序#include "stdafx.h"#include <iostream>using namespace std;//将有二个有序数列a[first...mid]和a[mid...last]合并。template<class T>void merge(T data[], int first, int mid, int last, T temp[]){int low1 = first, hight1 = mid;int low2 = mid + 1, hight2 = last;int k = first;while (low1 <= hight1 && low2 <= hight2){if (data[low1] < data[low2]){temp[k++] = data[low1++];}else{temp[k++] = data[low2++];}}while (low1 <= hight1){temp[k++] = data[low1++];}while (low2 <= hight2){temp[k++] = data[low2++];}for (int i = first; i <= last; i++){data[i] = temp[i];}}/*//递归template<class T>void mergesort(T data[], int first, int last, T temp[]){if (first < last){int mid = (first + last) / 2;mergesort(data, first, mid, temp); //左边有序mergesort(data, mid + 1, last, temp); //右边有序merge(data, first, mid, last, temp); //再将二个有序数列合并}}*///非递归template<class T>void mergesort(T data[], int first, int last, T temp[]){int length = 1;int arrsize = last - first + 1;while (length <= arrsize){for (int i = 0; i + 2 * length < arrsize; i += 2 * length){int mid = (i + (i + 2 * length - 1)) / 2;merge(data, i, mid, i + 2 * length - 1, temp);}length *= 2;}}template<class T>bool MergeSort(T data[], int n){T* temp = new T[n];if (NULL == temp)return false;mergesort(data, 0, n - 1, temp);delete[] temp;temp = NULL;return true;}template<class T>void Sprint(T data[], int n){for (int i = 0; i < n; i++){cout << data[i] << " ";}cout << endl;}int _tmain(int argc, _TCHAR* argv[]){int data[] = { 12, 0, 3, 5, 1, 4, 6, 2, 11 };int n = sizeof(data) / sizeof(int);MergeSort(data, n);Sprint(data, n);return 0;}
归并排序应用
题:在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序数对。一个排列中逆序的总数就称为这个排列的逆序数。如{2,4,3,1}中,2和1,4和3,4和1,3和1是逆序数对,因此整个数组的逆序数对个数为4,现在给定一数组,要求统计出该数组的逆序数对个数
代码实例
#include "stdafx.h"#include <iostream>using namespace std;int g_nCount = 0;//将有二个有序数列a[first...mid]和a[mid...last]合并。template<class T>void merge(T data[], int first, int mid, int last, T temp[]){int low1 = first, hight1 = mid;int low2 = mid + 1, hight2 = last;int k = first;while (low1 <= hight1 && low2 <= hight2){if (data[low1] < data[low2]){temp[k++] = data[low1++];}else{temp[k++] = data[low2++];g_nCount += hight1 - low1 + 1;}}while (low1 <= hight1){temp[k++] = data[low1++];}while (low2 <= hight2){temp[k++] = data[low2++];}for (int i = first; i <= last; i++){data[i] = temp[i];}}//递归template<class T>void mergesort(T data[], int first, int last, T temp[]){if (first < last){int mid = (first + last) / 2;mergesort(data, first, mid, temp); //左边有序mergesort(data, mid + 1, last, temp); //右边有序merge(data, first, mid, last, temp); //再将二个有序数列合并}}template<class T>bool MergeSort(T data[], int n){T* temp = new T[n];if (NULL == temp)return false;mergesort(data, 0, n - 1, temp);delete[] temp;temp = NULL;return true;}template<class T>void Sprint(T data[], int n){for (int i = 0; i < n; i++){cout << data[i] << " ";}cout << endl;}int _tmain(int argc, _TCHAR* argv[]){int data[] = { 2, 4, 3, 1 };int n = sizeof(data) / sizeof(int);MergeSort(data, n);//Sprint(data, n);cout << g_nCount << endl;return 0;}
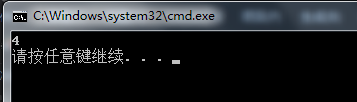
结果:


































还没有评论,来说两句吧...