最小生成树-Kruskal(克鲁斯卡尔)算法

﹏ヽ暗。殇╰゛Y 2022-05-15 06:42 268阅读 0赞

*  # 最小生成树-Kruskal(克鲁斯卡尔)算法 #

--------------------

*  ## 简述生成树： ##

### 生成树： ###

**给定一个无向图(顶点间连线不带方向)，如果它*任意两个顶点都联通并且是一棵树*，那么我们就称之为生成树(Spanning Tree)**

### 最小生成树： ###

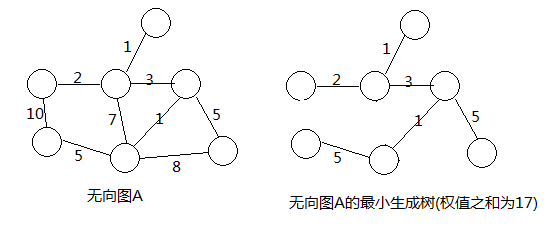
如果是带权值的无向图，那么**权值之和最小的生成树**，我们就称之为最小生成树(MST, Minimum Spanning Tree)

![Center][]

### 应用： ###

最小生成树广泛应用于城市间道路建设的优化，通信网络最优铺设等，将网络站点或者城市看成无向图中的顶点，把每条道路、网线的成本作为权值，从而计算出建设的最小成本

*  ## MST实现算法-Kruskal ##

### 算法思想： ###

**Kruskal 是基于贪心的最小生成树实现算法，通过将所有边的权值排序，按从小到大的顺序取出，如果边的端点不属于同一个集合（未联通，该道路需要建设），那么将这两个端点所属的两个集合合并（建设道路后，端点联通），直到所有点属于一个集合为止**

### 算法基础： ###

为了高效查取端点的集合归属，用到了并查集，可以说 Kruskal是基于并查集的贪心算法

**并查集传送门：[数据结构-并查集][-]**

### 算法流程： ###

**a.起始时每个顶点作为单元素集合**

**b.对所有边按权值（成本）进行排序**

**c.按小到大顺序，取出边（u，v），如果u v 不属于同一集合，将u，v 所属集合合并**

**d.重复c，直到所有边遍历完，或者所有顶点连通：假设有m个点，合并的边数n，最优连通的充要条件 n=m-1**

*  ## Kruskal模板 ##

#include<iostream>
    #include<algorithm>
    using namespace std;
    #define MAX_SIZE 105
    struct Road   //边
    {
        int Begin;
        int End;
        int Price;
        bool operator<(Road b)const
        {
            return this->Price<b.Price;
        }
    };
    
    Road Road_List[MAX_SIZE];
    int Village[MAX_SIZE];  //顶点
    int Rank[MAX_SIZE];   //记录高度
     
    void Init(int n)   //初始化
    {
        for(int i=1;i<=n;i++)
        {
            Rank[i]=0;
            Village[i]=-1;
        }
    }
     
    int Find(int x)   //查找根
    {
        int root=x;
        while(Village[root]!=-1)   
            root=Village[root];
        while(x!=root)    //将间接连在根上的结点改成直接连于根，提高查找效率
        {
            int temp=Village[x];
            Village[x]=root;
            x=temp;
        }
        return root;
    }
    
    int Combine(int a,int b)
    {
        int a_root=Find(a);
        int b_root=Find(b);
        if(a_root==b_root)    //属于同一集合，不做操作
            return 0;
        
        //合并 
        if(Rank[a_root]<Rank[b_root])   //树a_root 比b_root矮，放置在b下
            Village[a_root]=b_root;
        else
        {
            Village[b_root]=a_root;  //...
            if(Rank[a_root]==Rank[b_root]) //两树一样高时，合并后a树会变高
                Rank[a_root]++;
        }
        return 1;
    }
    
    int Kruskal(int n,int m)   //n为边总数，m为顶点总数
    {
        int Road_Num=0;   //已合并的边数
        int Min_Cost=0;   //最低总成本
        sort(Road_List+1,Road_List+n+1);
        for(int i=1;i<=n&&Road_Num!=m-1;i++)     
        {
            if(Combine(Road_List[i].Begin,Road_List[i].End))  //边两端顶点还未连通
            {
                Min_Cost+=Road_List[i].Price;
                Road_Num++;
            }
        }
        if(Road_Num<m-1)    //Road_Num<m-1 给定的边数无法满足将所有顶点连通
            return -1;
        else
            return Min_Cost;
    }

*  ## 基础题练手： ##

### [最小生成树(Kruskal)POJ 1258 Agri-Net][Kruskal_POJ 1258 Agri-Net] ###

### [最小生成树(Kruskal)HDU 1863-畅通工程][Kruskal_HDU 1863-] ###

*  ## 参考文章： ##

### [刻苦驴啊- 学习图论（五）——最小生成树][- 1] ###

### [Enstein\_Jun-最小生成树之Kruskal算法][Enstein_Jun-_Kruskal] ###

[Center]: /images/20220515/823c712c37af4985aaa94a746a894f50.png
[-]: https://blog.csdn.net/SZU_Crayon/article/details/81986258
[Kruskal_POJ 1258 Agri-Net]: https://blog.csdn.net/SZU_Crayon/article/details/82079203
[Kruskal_HDU 1863-]: https://blog.csdn.net/SZU_Crayon/article/details/82079306
[- 1]: https://blog.csdn.net/D5__J9/article/details/79950804
[Enstein_Jun-_Kruskal]: https://blog.csdn.net/luomingjun12315/article/details/47700237