最小生成树-kruskal算法（克鲁斯卡尔算法）
克鲁斯卡尔解决最小生成树的问题，克鲁斯卡尔算法的思想是将所有边按照权值，从小到大排列起来，然后依次从小到大选择边，如果选择的边会造成回路，那么放弃选择一个更大的边。
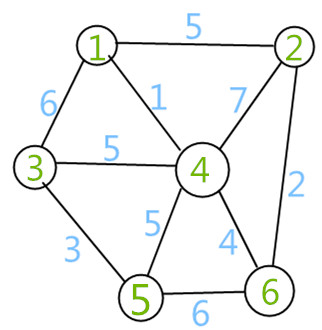
如图所示：首先获取<1,4>，边权值为1；
下一步获取<2,6>,权值为2；
下一步获取<3,5>，权值为3;
下一步获取<4,6>，权值为4;
最后获取<3,4>，权值为5;
这样最小生成树就完成了。
相关阅读
朱雀
快来打我*相关 克鲁斯卡尔算法(Kruskal)
应用场景-公交站问题 1. 某城市新增7个站点(A, B, C, D, E, F, G) ，现在需要修路把7个站点连通 2. 各个站点的距离用边线表示(权) ，比如 A
相关 最小生成树算法-克鲁斯卡尔（kruskal）算法
include <stdio.h> define MaxSize 100 define INF 32767 //INF表示∞ define MA
相关 645-Kruskal克鲁斯卡尔算法
Kruskal克鲁斯卡尔算法理论 Kruskal克鲁斯卡尔算法是处理边的，所以在稀疏的边比较少的连通网中，用Kruskal克鲁斯卡尔算法效率就比较高。 在边比较多的连
相关 数据结构——最小生成树之克鲁斯卡尔算法(Kruskal)
最小生成树算法 prime算法和克鲁斯卡尔算法 克鲁斯卡尔算法 思路 优先队列+并查集 Kuskal算法 【算法简介】：上一篇中的Prime算法是一种“加点式的算法
相关 C++ 最小生成树之kruskal（克鲁斯卡尔）算法
最小生成树之kruskal（克鲁斯卡尔）算法 kruskal算法：同样解决最小生成树的问题，和prim算法不同，kruskal算法采用了边贪心的策略，思想要比pri
相关 最小生成树--克鲁斯卡尔算法
算法描述： 假设连通网N=（V,\{ E \}），则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，\{ \}），图中每一个顶点自成
相关 最小生成树-kruskal算法（克鲁斯卡尔算法）
克鲁斯卡尔解决最小生成树的问题，克鲁斯卡尔算法的思想是将所有边按照权值，从小到大排列起来，然后依次从小到大选择边，如果选择的边会造成回路，那么放弃选择一个更大的边。 
左手的ㄟ右手相关 最小生成树-Kruskal(克鲁斯卡尔)算法
最小生成树-Kruskal(克鲁斯卡尔)算法 -------------------- 简述生成树： 生成树： 给定一个无向图(顶点间连线不带方
还没有评论，来说两句吧...