二叉树（三）——二叉树的遍历

约定不等于承诺〃 2022-05-25 08:25 208阅读 0赞

今天我来说一说二叉树的几种遍历。在我看来二叉树的遍历主要有四种：

（1）层次遍历

（2）前序遍历

（3）中序遍历

（4）后序遍历

下面我将具体地介绍一下这几种遍历方式

书接上回（数据结构——基本代码的实现），我已经建立了一个二叉树那么现在我就根据这棵已有的二叉树来进行讲解。

首先是层次遍历。层次遍历的思想主要是利用队列的特性——先进先出。

首先我将头结点进行判断，当然头结点为空时抛出异常。其次我将头结点的非空左右孩子入队。这个时候我们的队列就建立起来了。那么入队的顺序我将用一个图来简要解释

![70][]

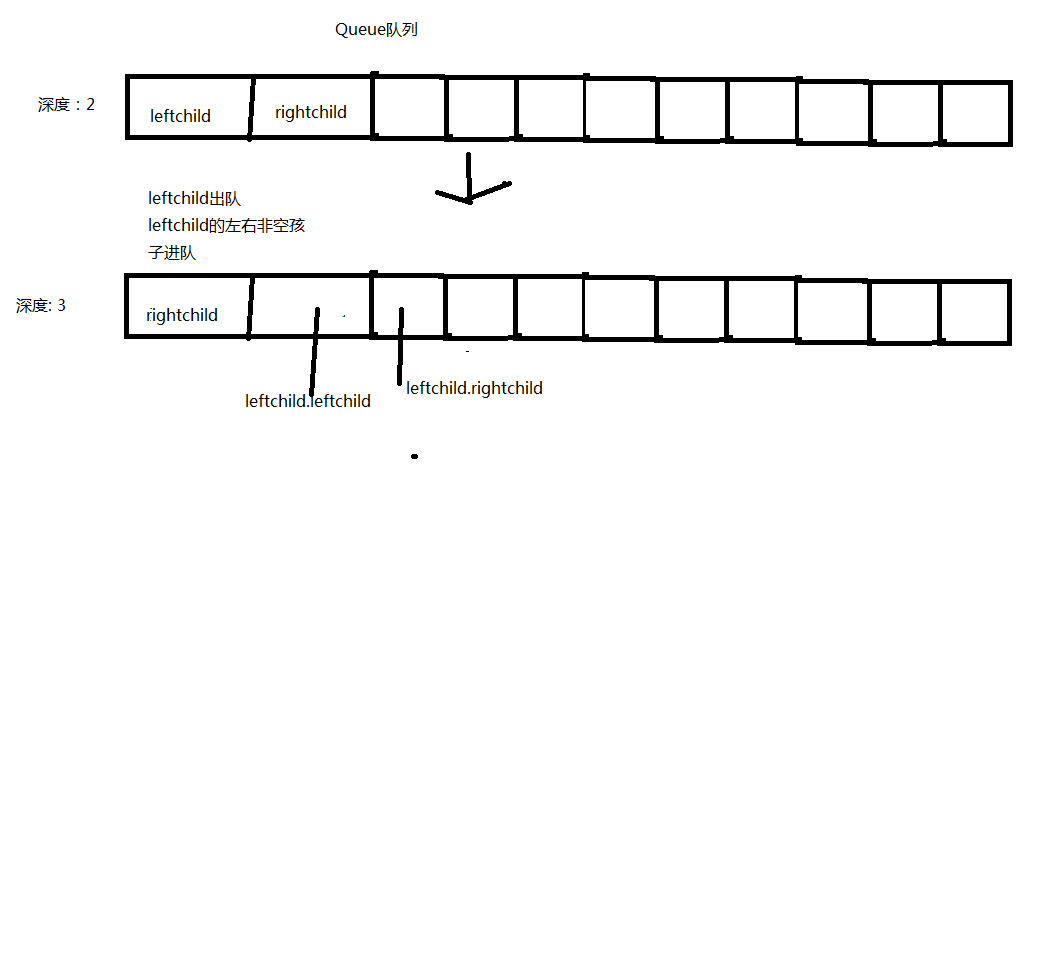
从这个图，我们可以看到。左右孩子按照顺序依次入队进行层次遍历。

下面是我的java代码。

private void levelOrder(TreeNode node) {
     if(node==null){
     try {
     throw new Exception("该树为空");
     } catch (Exception e) {
     // TODO Auto-generated catch block
     e.printStackTrace();
     }
     }
     System.out.println(node.data+" ");
     Queue<TreeNode> queue = new LinkedList<TreeNode>();
     if(node.leftChild!=null){
     queue.add(node.leftChild);
     System.out.println(node.leftChild.data+" ");
     }
     if(node.rightchild!=null){
     queue.add(node.rightchild);
     System.out.println(node.rightchild.data+" ");
     }
     while(!queue.isEmpty()){
     TreeNode n = queue.remove();
     if(n.leftChild!=null){
     queue.add(n.leftChild);
     System.out.println(n.leftChild.data+" ");
     }
     if(n.rightchild!=null){
     queue.add(n.rightchild);
     System.out.println(n.rightchild.data+" ");
     }
     }
     }

这是层次遍历也是最简单的一种

下面我们来说一说前序遍历。

前序遍历分为两种，一种是递归遍历，一种是非递归遍历。

递归遍历的代码非常简单。

private void preOrder(TreeNode node){
    			if(node==null){
    				return;
    			}
    			System.out.println("preOrder---->"+node.data);
    			preOrder(node.leftChild);
    			preOrder(node.rightchild);
    	}

它遵从的就是根  左  右 的遍历方式。先去遍历根节点，然后把根节点的左孩子当做新的根节点继续进行遍历操作。知道最后一个左孩子没有左孩子时，再去看它的右孩子，倘若它没有右孩子则关于这个结点的本次前序遍历结束。其他结点以此类推。以这个思想为基础。可以推出非递归的前序遍历方式。

private void nonPreOrder(TreeNode node) {
    		if(node == null){
    			return;
    		}
    		Stack<TreeNode> stack = new Stack<TreeNode>();
    		stack.push(node);
    		while(!stack.isEmpty()){
    			//进栈和出栈
    			TreeNode n = stack.pop();//出栈操作
    			System.out.println("nonPreOrder---->"+n.data);
    			if(n.rightchild!=null){
    				stack.push(n.rightchild);
    			}
    			if(n.leftChild!=null){
    				stack.push(n.leftChild);
    			}
    			
    		}
    	}

这个用到了栈的思想。首先我们将非空的根节点入栈。当栈不为空时。将栈的第一个元素的右孩子入栈，然后将左孩子入栈。

原因很简单，因为栈的特性是先入后出的。这个很像我们的层次遍历。不同的时以头结点先入栈，然后就开始了遍历。

这个我也可以用一副图来表示

![70 1][]

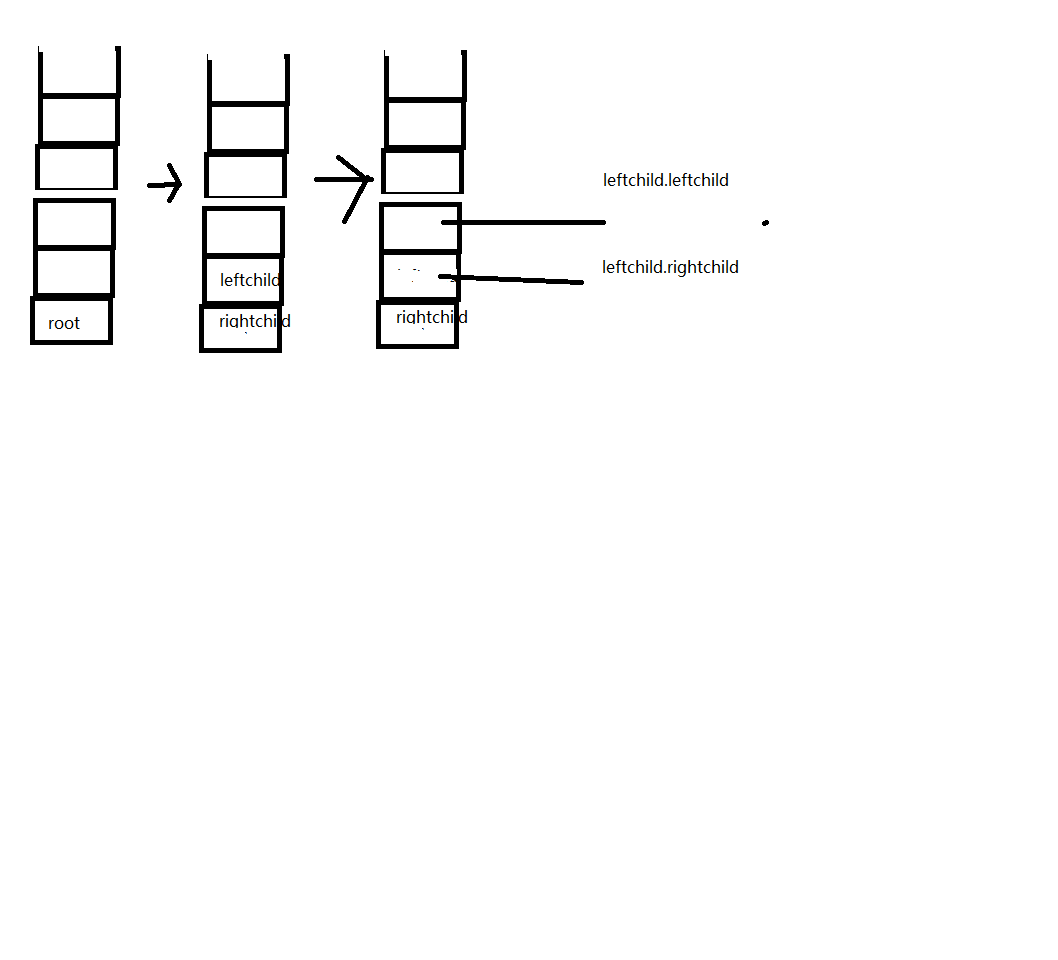
说完前序遍历，来看看中序遍历。中序遍历思想较为复杂。

依照的是左 根  右  同样是有递归和非递归的方式。先看看非递归的方式

private void middleOrder(TreeNode node) {
    		if(node==null){
    			return;
    		}
    		middleOrder(node.leftChild);
    		System.out.println("middleOrder---->"+node.data);
    		middleOrder(node.rightchild);
    		
    	}

这个代码阐述了中序遍历的思想，一直中序遍历左孩子，左孩子的左孩子......到最后的左孩子没有左孩子时，它就是根节点，将其输出。然后同样的中序遍历它的右孩子。

那么来看看非递归的算法。

public void nonMiddleOrder(TreeNode node){
    		if(node==null){
    			return ;
    		}
    		Stack<TreeNode> stack = new Stack<TreeNode>();
    		TreeNode n = node;
    		/**
    		 * 首先一个结点将所有的左子树进行入栈，当最后一个左子树没有左子树时，同样的方法中序遍历右子树
    		 */
    		while(!stack.isEmpty()||n!=null){
    			while(n!=null){
    				stack.push(n);
    				n=n.leftChild;
    			}
    			if(!stack.empty()){
    				n = stack.pop();
    				System.out.println("nonMiddle--->"+n.data);
    				n = n.rightchild;
    			}
    			
    		}
    		
    	}

如我们所说的那样，是首先去沿着树的左侧一直走到底然后再往上走去遍历。那么同样利用了栈。

把这棵树最左侧的所有子树都放进栈。所有左侧子树都入栈之后，将栈的头结点也就是我刚才所说的那个没有左子树的子树出栈，将其值进行输出。令n 指向它的右孩子。同样进行最外面的while循环，进入之后，如果右孩子 非空，那么把它的左孩子，左孩子的左孩子.........同样进行入栈操作。      依次类推进行剩下的操作。

最后一个是后序遍历，同样有递归和非递归算法。顺序是左  右  根

private void postOrder(TreeNode node) {
    			if(node ==null){
    				return ;
    			}
    			postOrder(node.leftChild);
    			postOrder(node.rightchild);
    			System.out.println("postOrder---->"+node.data);
    	}

先沿根节点的左孩子，左孩子的左孩子.........走到底,然后遍历最后一个孩子的左孩子和右孩子，当它的度为0时，将其进行遍历输出。由此我们引出了它的非递归算法。

private void nonPostOrder(TreeNode node) {
    		if(node ==null){
    			return ;
    		}
    		Stack<TreeNode> stack =new Stack<TreeNode>();
    		TreeNode current = node;//当前访问结点
    		TreeNode lastNode = null;//上一次访问结点
    		while(current!=null){//将当前访问结点一直已到最底侧，此时current为空
    			stack.push(current);
    			current = current.leftChild;
    		}
    		while(!stack.isEmpty()){
    			current = stack.pop();//由于current结点是空的，所以将栈顶结点赋给current，并出栈。
    			/**
    			 * 一个根节点被访问的前提是，它的右子树已经被访问过或者时它的右子树刚刚被访问过
    			 */
    			if(current.rightchild==null||current.rightchild ==lastNode){
    				System.out.println("nonPostOrder--->"+current.data);
    				lastNode = current;
    			}
    			else{
    				//根节点再次入栈
    				stack.push(current);
    				//进入右子树，此时右子树一定不为空
    				current = current.rightchild;
    				while(current!=null){
    					stack.push(current);
    					current = current.leftChild;
    				}
    			}
    		}
    	}

同样我们要利用栈的思想，首先我们先定义两个节点current,lastNode。用来表示当前访问结点和上一次循环访问的结点。

首先我们需要将根节点的左孩子，左孩子的左孩子........依次入栈。

当栈不为空时，令current指向栈顶元素。当我们要输出根节点的数值时。需要满足一些条件

就是它没有右子树或者它的右子树刚刚被访问过。

这时候将lastNode的引用指向当前访问结点current

否则，即当前结点具有右孩子

根节点再次入栈，进入右子树，将右子树的左孩子，左孩子的左孩子进行入栈操作。

这就是二叉树的几种遍历方式。下一次我将实现的是查找二叉树，也就是我们常说的红黑树。

[70]: /images/20220525/eaed13778b194d8f8f458ccbe11c0cfb.png
[70 1]: /images/20220525/31bd9ddb1eae443ea1051783a373a8e1.png