二叉树 二叉树遍历 通过二叉树遍历求得二叉树

偏执的太偏执、 2022-12-04 01:08 442阅读 0赞

什么是二叉树

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分 [1] 。
二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点

二叉树的遍历

前序遍历

遍历二叉树，先打印根节点的遍历方式

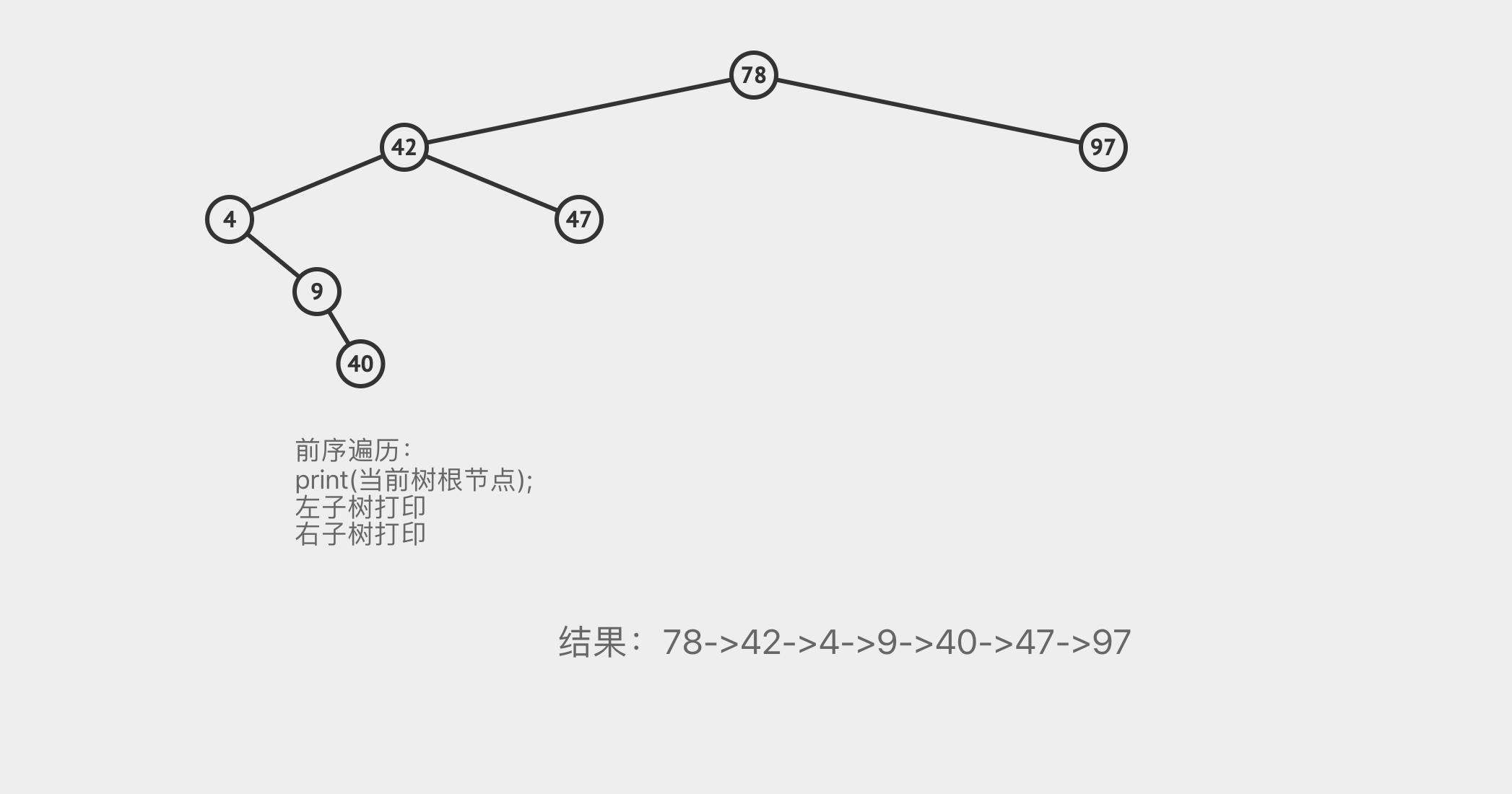
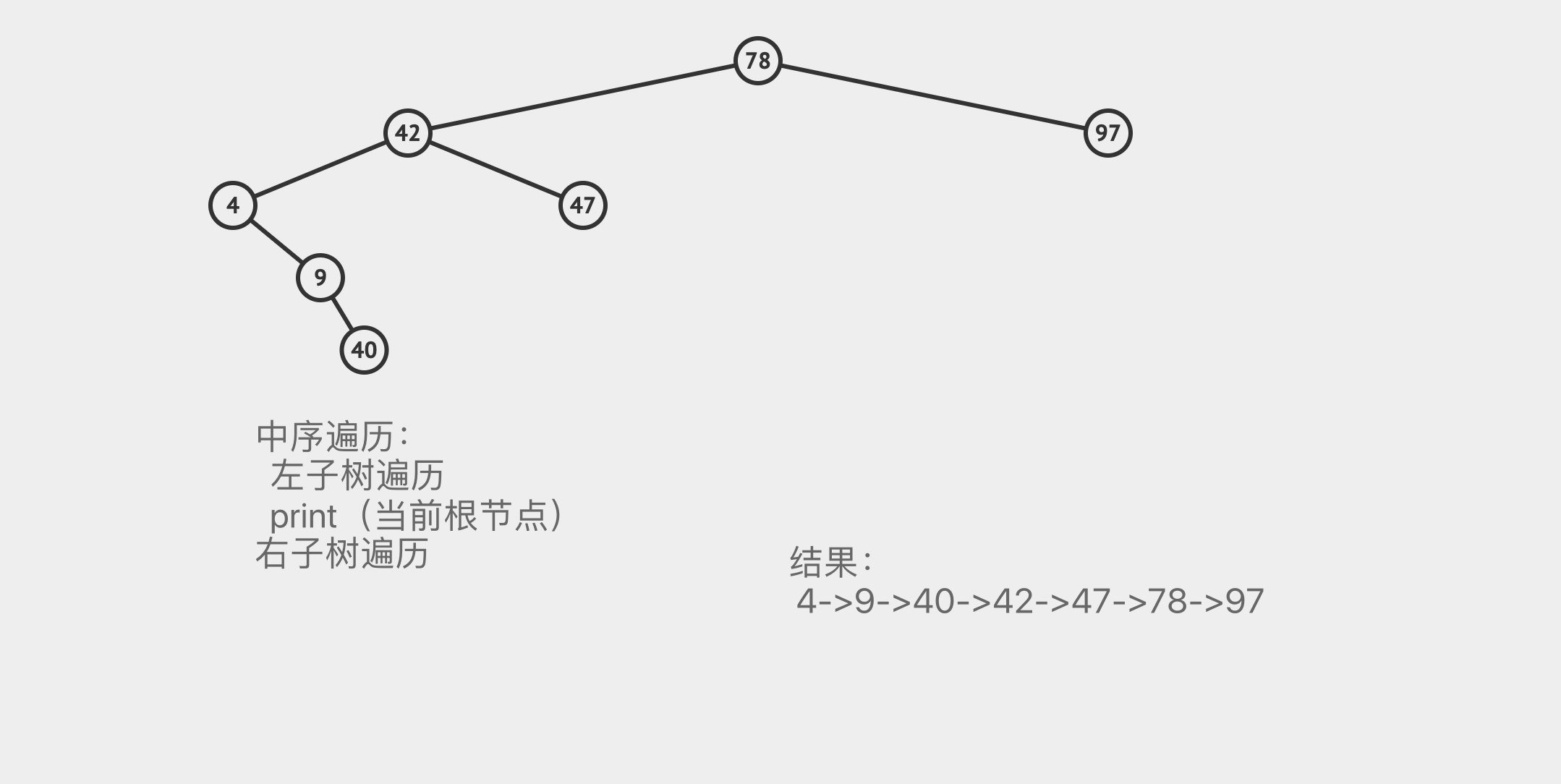
前序遍历输出

中序遍历

遍历二叉树，在中间打印根节点的遍历方式
前序遍历输出

后序遍历输出

遍历二叉树，最后打印根节点的遍历方式

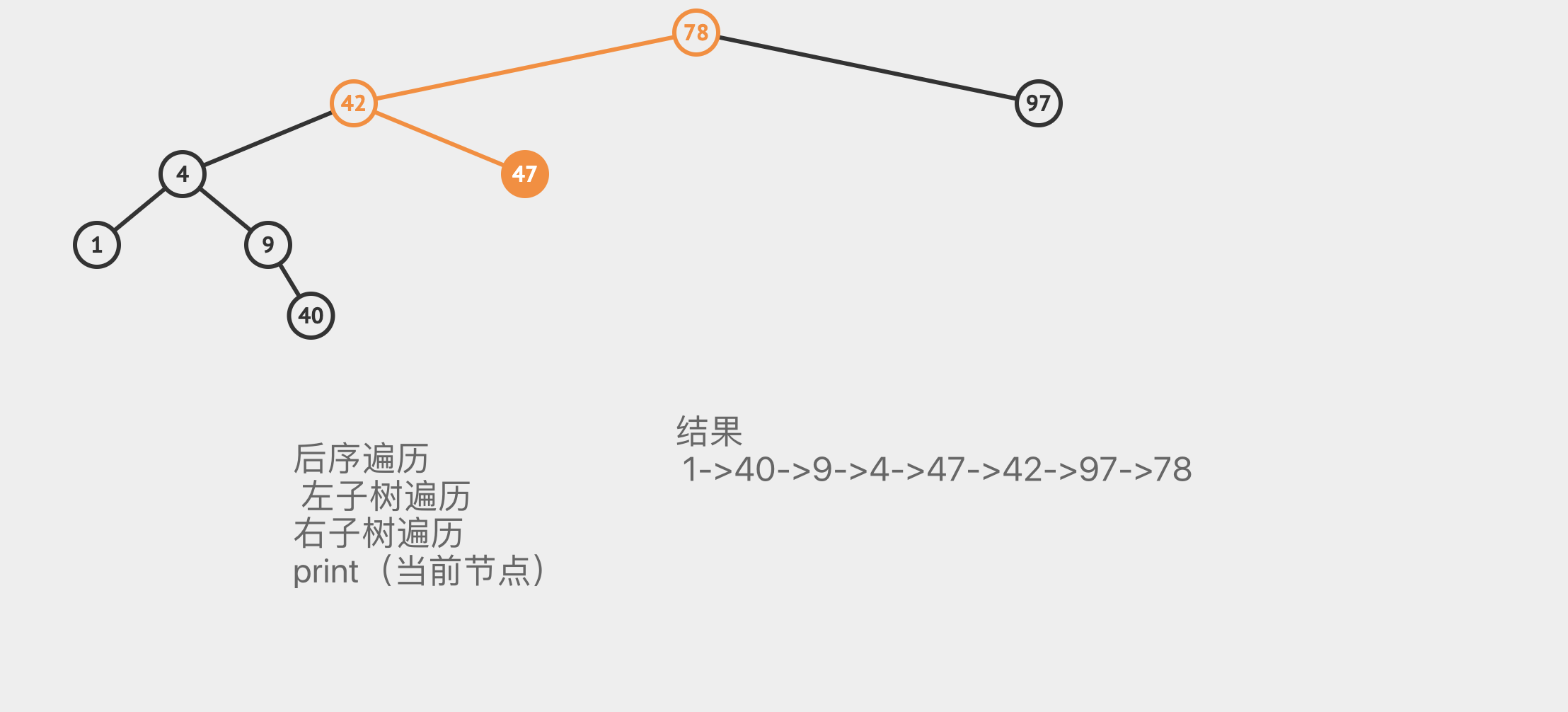
后序遍历输出

强烈推荐数据结构练习网站

https://visualgo.net/zh

通过两种遍历确定二叉树（其中一种必须为中序遍历）

举列
步骤

  1. 通过前序遍历 确定第一个根节点（当前序列第一个）
  2. 根据第一个根节点 在中序遍历中确定 左右子树
  3. 在确定的左树中 通过前序遍历找到它到根节点
  4. 在通过左树的根节点 在中序遍历中确定 左右子树
  5. 反复循环

发表评论

表情：
评论列表 （有 0 条评论，442人围观）

还没有评论，来说两句吧...

相关阅读

    相关 遍历二叉树

    遍历二叉树 今天我们学习了二叉树，现在我就基于二叉树的递归定义来说一说遍历二叉树的三种方法：先序、中序和后序。 根据二叉树的递归定义可知，二叉树是由3个基本单元组成：根结点

    傷城~傷城~/ 0 赞/ 468 阅读

    相关 二叉树遍历

    前序遍历（左中右）ABDGHCEIF ![前序遍历][70] 中序遍历（左根右）GDHBAEICF![中序遍历][70 1] 后序遍历（左右根）GHDBIEFCA![

    Bertha 。Bertha 。/ 0 赞/ 531 阅读

    相关 二叉树遍历

    二叉树是数据结构中很重要的一个章节，很多同学反应很难，今天我就把我平时的经验给大家讲解一下，今天讲一下二叉树的遍历 工具/原料 ● 数据结构知识 ● 了解树的定义

    爱被打了一巴掌爱被打了一巴掌/ 0 赞/ 417 阅读