TOJ 1705 Dining 最大流-蒲公英云

TOJ 1705 Dining 最大流

描述

Cows are such finicky eaters. Each cow has a preference for certain foods and drinks, and she will consume no others.

Farmer John has cooked fabulous meals for his cows, but he forgot to check his menu against their preferences. Although he might not be able to stuff everybody, he wants to give a complete meal of both food and drink to as many cows as possible.

Farmer John has cooked F (1 ≤ F ≤ 100) types of foods and prepared D (1 ≤ D ≤ 100) types of drinks. Each of his N (1 ≤ N ≤ 100) cows has decided whether she is willing to eat a particular food or drink a particular drink. Farmer John must assign a food type and a drink type to each cow to maximize the number of cows who get both.

Each dish or drink can only be consumed by one cow (i.e., once food type 2 is assigned to a cow, no other cow can be assigned food type 2).

输入

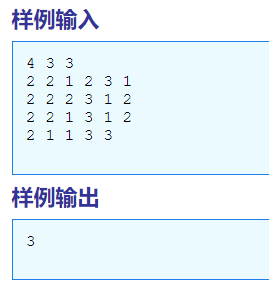
Line 1: Three space-separated integers: N, F, and D
Lines 2..N+1: Each line i starts with a two integers Fi and Di, the number of dishes that cow i likes and the number of drinks that cow i likes. The next Fi integers denote the dishes that cow i will eat, and the Di integers following that denote the drinks that cow i will drink.

输出

Line 1: A single integer that is the maximum number of cows that can be fed both food and drink that conform to their wishes

20180411210157616

提示

One way to satisfy three cows is:
Cow 1: no meal
Cow 2: Food #2, Drink #2
Cow 3: Food #1, Drink #1
Cow 4: Food #3, Drink #3
The pigeon-hole principle tells us we can do no better since there are only three kinds of food or drink. Other test data sets are more challenging, of course.

这道题建图需要思考一下的，我以我神乎其技的画技给大家画了这个模拟图….

大概就是设置一个S,T，然后要2个牛，左边的牛连吃的，右边的牛连喝的，然后让两头牛连一下。

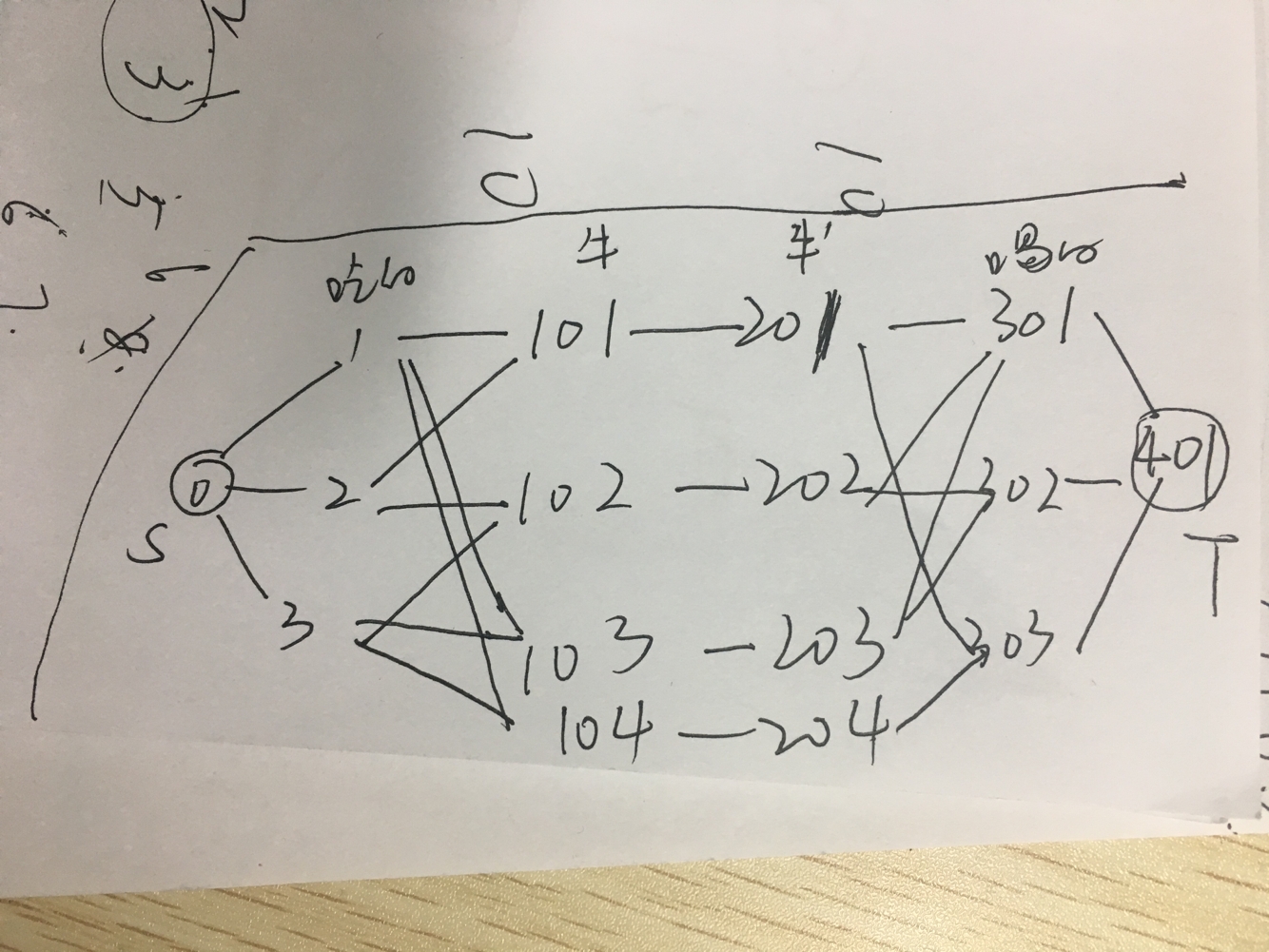
20180411210321958

注意坐标哦，N最大100，所以每次都要+100哦。

然后就用最大流求一下就好啦~~

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<string>
#include<algorithm>
#include<map>
#include<queue>
#include<vector>
using namespace std;
const int inf=0x7f7f7f7f;
int n,m,k,G[505][505],flow[505],pre[505];
queue<int> q;
int bfs(int s,int t)
{
    while(!q.empty())
    q.pop();
    memset(pre,-1,sizeof pre);
    pre[s]=0,flow[s]=inf;
    q.push(s);
    while(!q.empty())
    {
        int p=q.front();
        q.pop();
        if(p==t)break;
        for(int u=1;u<=n;u++)
        {
            if(u!=s&&G[p][u]>0&&pre[u]==-1)
            {
                pre[u]=p;
                flow[u]=min(flow[p],G[p][u]);
                q.push(u);
            }
        }
    }
    if(pre[t]==-1)return -1;
    return flow[t];
}
int EK(int s,int t)
{
    int delta=0,tot=0;
    while(1)
    {
        delta=bfs(s,t); 
        if(delta==-1)break;
        int p=t;
        while(p!=s)
        {
            G[pre[p]][p]-=delta;
            G[p][pre[p]]+=delta;
            p=pre[p];
        }
        tot+=delta;
    }
    return tot;
}
int main()
{
    int i,j,l,t,tt,x;
    while(scanf("%d%d%d",&n,&m,&k)!=EOF)
    {
        memset(G,0,sizeof G);
        memset(flow,0,sizeof flow);    
        //0为超级源点，401为超级汇点 
        for(i=1;i<=m;i++)
        G[0][i]=1;
        for(i=1;i<=k;i++)
        G[i+300][401]=1;
        for(i=1;i<=n;i++)
        G[i+100][i+200]=1;
        for(i=1;i<=n;i++)
        {
            scanf("%d%d",&t,&tt);
            for(j=0;j<t;j++)
            {
                scanf("%d",&x);
                G[x][i+100]=1;
            }
            for(l=0;l<tt;l++)
            {
                scanf("%d",&x);
                G[i+200][x+300]=1;
            }
        }
        n=401;
        printf("%d\n",EK(0,401));
    }
}