【深度学习】RNN循环神经网络Python简单实现-蒲公英云

前言

代码可在Github上下载:代码下载
循环神经网络是一种时间序列预测模型，多应用在自然语言处理上。
原理网上是有很多的，不展开解释，本文基于一个二进制加法，进行python实现。
其实python代码并非本人实现
具体参考两篇博客，第一篇是英语原文，第二篇是译文。
https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
http://blog.csdn.net/zzukun/article/details/49968129

原理

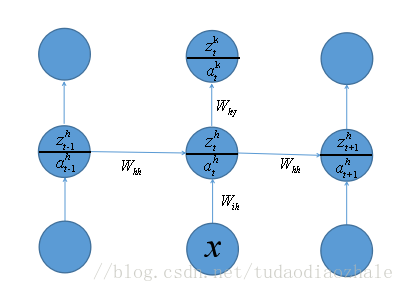
RNN结构图

前向传播
z h = w i h x + w h h a h − 1 a h = σ ( z h ) z k = w h y a h a k = σ ( z k ) \begin{array}{l} {z^h} = {w_{ih}}x + {w_{hh}}{a^{h - 1}}\\ {a^h} = \sigma \left( { {z^h}} \right)\\ {z^k} = {w_{hy}}{a^h}\\ {a^k} = \sigma \left( { {z^k}} \right) \end{array} zh=wihx+whhah−1ah=σ(zh)zk=whyahak=σ(zk)

反向传播
δ t k = ∂ E ∂ a k ∂ a k ∂ z k = ( y t − a t k ) × ( z k ) ′ = ( y t − a t k ) × ( z k × ( 1 − z k ) ) δ T h = ∂ E ∂ a T k ∂ a T k ∂ z T k ∂ z T k ∂ a T h ∂ a T h ∂ z T h = ( W h y ) T δ T k × ( a h ( 1 − a h ) ) δ t h = ∂ E ∂ a t k ∂ a t k ∂ z t k ∂ z t k ∂ a t h ∂ a t h ∂ z t h + ∂ E ∂ a t + 1 k ∂ a t + 1 k ∂ z t + 1 k ∂ z t + 1 k ∂ a t + 1 h ∂ a t + 1 h ∂ z t + 1 h ∂ z t + 1 h ∂ a t h ∂ a t h ∂ z t h = ( ( W h h ) T δ t + 1 h + ( W h y ) T δ t k ) ∂ a t h ∂ z t h = ( ( W h h ) T δ t + 1 h + ( W h y ) T δ t k ) × ( a h ( 1 − a h ) ) W i h = W i h − η δ t h ( x t ) T W h h = W h h − η δ t h ( a t − 1 h ) T W h y = W h y − η δ t k ( a t h ) T \begin{array}{l} \delta _t^k = \frac{ {\partial E}}{ {\partial {a^k}}}\frac{ {\partial {a^k}}}{ {\partial {z^k}}} = ({y_t} - a_t^k) \times \left( { {z^k}} \right)' = ({y_t} - a_t^k) \times \left( { {z^k} \times \left( {1 - {z^k}} \right)} \right)\\ \delta _T^h = \frac{ {\partial E}}{ {\partial a_T^k}}\frac{ {\partial a_T^k}}{ {\partial z_T^k}}\frac{ {\partial z_T^k}}{ {\partial a_{\rm{T}}^h}}\frac{ {\partial a_T^h}}{ {\partial z_{\rm{T}}^h}} = {\left( { {W_{hy}}} \right)^T}\delta _T^k \times \left( { {a^h}\left( {1 - {a^h}} \right)} \right)\\ {\delta _t^h = \frac{ {\partial E}}{ {\partial a_t^k}}\frac{ {\partial a_t^k}}{ {\partial z_t^k}}\frac{ {\partial z_t^k}}{ {\partial a_t^h}}\frac{ {\partial a_t^h}}{ {\partial z_t^h}} + \frac{ {\partial E}}{ {\partial a_{t + 1}^k}}\frac{ {\partial a_{t + 1}^k}}{ {\partial z_{t + 1}^k}}\frac{ {\partial z_{t + 1}^k}}{ {\partial a_{t{\rm{ + }}1}^h}}\frac{ {\partial a_{t{\rm{ + }}1}^h}}{ {\partial z_{t + 1}^h}}\frac{ {\partial z_{t + 1}^h}}{ {\partial a_t^h}}\frac{ {\partial a_t^h}}{ {\partial z_t^h}}}\\ {\rm{ }} = \left( { { {\left( { {W_{hh}}} \right)}^T}\delta _{t + 1}^h + { {\left( { {W_{hy}}} \right)}^T}\delta _t^k} \right)\frac{ {\partial a_t^h}}{ {\partial z_t^h}}\\ {\rm{ }} = \left( { { {\left( { {W_{hh}}} \right)}^T}\delta _{t + 1}^h + { {\left( { {W_{hy}}} \right)}^T}\delta _t^k} \right) \times \left( { {a^h}\left( {1 - {a^h}} \right)} \right)\\ {W_{ih}} = {W_{ih}} - \eta \delta _t^h{\left( { {x_t}} \right)^T}\\ {W_{hh}} = {W_{hh}} - \eta \delta _t^h{\left( {a_{t - 1}^h} \right)^T}\\ {W_{hy}} = {W_{hy}} - \eta \delta _t^k{\left( {a_t^h} \right)^T} \end{array} δtk=∂ak∂E∂zk∂ak=(yt−atk)×(zk)′=(yt−atk)×(zk×(1−zk))δTh=∂aTk∂E∂zTk∂aTk∂aTh∂zTk∂zTh∂aTh=(Why)TδTk×(ah(1−ah))δth=∂atk∂E∂ztk∂atk∂ath∂ztk∂zth∂ath+∂at+1k∂E∂zt+1k∂at+1k∂at+1h∂zt+1k∂zt+1h∂at+1h∂ath∂zt+1h∂zth∂ath=((Whh)Tδt+1h+(Why)Tδtk)∂zth∂ath=((Whh)Tδt+1h+(Why)Tδtk)×(ah(1−ah))Wih=Wih−ηδth(xt)TWhh=Whh−ηδth(at−1h)TWhy=Why−ηδtk(ath)T

有了前向传播和反向传播的公式，就可以根据这个公式将RNN实现。代码解释在上面的两篇博客中都有所解释，只是他们并没有给出相应的公式，故将公式奉上。

代码实现

import copy, numpy as np
np.random.seed(0)
# sigmoid函数
def sigmoid(x):
    output = 1 / (1 + np.exp(-x))
    return output
# sigmoid导数
def sigmoid_output_to_derivative(output):
    return output * (1 - output)
# 训练数据生成
int2binary = {}
binary_dim = 8
largest_number = pow(2, binary_dim)
binary = np.unpackbits(
    np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]
# 初始化一些变量
alpha = 0.1 #学习率
input_dim = 2   #输入的大小
hidden_dim = 8  #隐含层的大小
output_dim = 1  #输出层的大小
# 随机初始化权重
synapse_0 = 2 * np.random.random((hidden_dim, input_dim)) - 1   #(8, 2)
synapse_1 = 2 * np.random.random((output_dim, hidden_dim)) - 1  #(1, 8)
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1  #(8, 8)
synapse_0_update = np.zeros_like(synapse_0) #(8, 2)
synapse_1_update = np.zeros_like(synapse_1) #(1, 8)
synapse_h_update = np.zeros_like(synapse_h) #(8, 8)
# 开始训练
for j in range(100000):
    # 二进制相加
    a_int = np.random.randint(largest_number / 2)  # 随机生成相加的数
    a = int2binary[a_int]  # 映射成二进制值
    b_int = np.random.randint(largest_number / 2)  # 随机生成相加的数
    b = int2binary[b_int]  # 映射成二进制值
    # 真实的答案
    c_int = a_int + b_int   #结果
    c = int2binary[c_int]   #映射成二进制值
    # 待存放预测值
    d = np.zeros_like(c)
    overallError = 0
    layer_2_deltas = list() #输出层的误差
    layer_2_values = list() #第二层的值（输出的结果）
    layer_1_values = list() #第一层的值（隐含状态）
    layer_1_values.append(copy.deepcopy(np.zeros((hidden_dim, 1)))) #第一个隐含状态需要0作为它的上一个隐含状态
    #前向传播
    for i in range(binary_dim):
        X = np.array([[a[binary_dim - i - 1], b[binary_dim - i - 1]]]).T    #(2,1)
        y = np.array([[c[binary_dim - i - 1]]]).T   #(1,1)
        layer_1 = sigmoid(np.dot(synapse_h, layer_1_values[-1]) + np.dot(synapse_0, X)) #(1,1)
        layer_1_values.append(copy.deepcopy(layer_1))   #(8,1)
        layer_2 = sigmoid(np.dot(synapse_1, layer_1))   #(1,1)
        error = -(y-layer_2)    #使用平方差作为损失函数
        layer_delta2 = error * sigmoid_output_to_derivative(layer_2)    #(1,1)
        layer_2_deltas.append(copy.deepcopy(layer_delta2))
        d[binary_dim - i - 1] = np.round(layer_2[0][0])
    future_layer_1_delta = np.zeros((hidden_dim, 1))
    #反向传播
    for i in range(binary_dim):
        X = np.array([[a[i], b[i]]]).T
        prev_layer_1 = layer_1_values[-i-2]
        layer_1 = layer_1_values[-i-1]
        layer_delta2 = layer_2_deltas[-i-1]
        layer_delta1 = np.multiply(np.add(np.dot(synapse_h.T, future_layer_1_delta),np.dot(synapse_1.T, layer_delta2)), sigmoid_output_to_derivative(layer_1))
        synapse_0_update += np.dot(layer_delta1, X.T)
        synapse_h_update += np.dot(layer_delta1, prev_layer_1.T)
        synapse_1_update += np.dot(layer_delta2, layer_1.T)
        future_layer_1_delta = layer_delta1
    synapse_0 -= alpha * synapse_0_update
    synapse_h -= alpha * synapse_h_update
    synapse_1 -= alpha * synapse_1_update
    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0
    # 验证结果
    if (j % 100 == 0):
        print("Error:" + str(overallError))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")