LCS/最长公共子序列/最长公共子串实现 Python/Java-蒲公英云

LCS/最长公共子序列/最长公共子串实现 Python/Java

参考

http://blog.csdn.net/u012102306/article/details/53184446
http://blog.csdn.net/hrn1216/article/details/51534607

最长公共子序列LCS

动态规划状态转移方程式
这里写图片描述

Python

递归

def LCS(a, b):
    if a == '' or b == '':
        return ''
    elif a[-1] == b[-1]:
        return LCS(a[:-1], b[:-1]) + a[-1]
    else:
        sol_a = LCS(a[:-1], b)
        sol_b = LCS(a, b[:-1])
        if len(sol_a) > len(sol_b):
            return sol_a
        return sol_b
if __name__ == "__main__":
    a = 'abc'
    print(a[::-1])
    print(LCS(a,a[::-1]))

动态规划

DP矩阵，前面多一行一列0，因为第一排计算需要用到dp[i - 1][j], dp[i][j -1]

之前的代码是多出了直接填写第二行第二列为1，但是也可以没必要，添加的可以参考Java版本的。

def lcs_dp(input_x, input_y):
        # input_y as column, input_x as row
        dp = [([0] * (len(input_y)+1)) for i in range(len(input_x)+1)]
        for i in range(1, len(input_x)+1):
            for j in range(1, len(input_y)+1):
                if input_x[i-1] == input_y[j-1]:  # 相等就加一
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:  # 不相等
                    dp[i][j] = max(dp[i - 1][j], dp[i][j -1])
        for dp_line in dp:
            print(dp_line)
        return dp[-1][-1]
print(lcs_dp('saibh','sibh'))
[0, 0, 0, 0, 0]
[0, 1, 1, 1, 1]
[0, 1, 1, 1, 1]
[0, 1, 2, 2, 2]
[0, 1, 2, 3, 3]
[0, 1, 2, 3, 4]
4

Java

动态规划

public static int lcs(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                c[i][j] = c[i-1][j-1] + 1;  
            } else {  
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);  
            }  
        }  
    }  
    return c[len1][len2];  
}

最长公共回文子串

动态规划状态转移方程式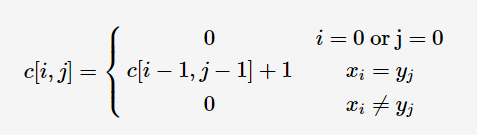
这里写图片描述

Python

动态规划
同上面相同：

if i == 0 or j == 0:  # 在边界上，自行+1
    dp[i][j] = 0

这句话可以省略，因为可以在循环钟推导出。

同时输出长度和字符串

class LCS3:
    def lcs3_dp(self, input_x, input_y):
        # input_y as column, input_x as row
        dp = [([0] * (len(input_y)+1)) for i in range(len(input_x)+1)]
        maxlen = maxindex = 0
        for i in range(1, len(input_x)+1):
            for j in range(1, len(input_y)+1):
                if input_x[i-1] == input_y[j-1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                    if dp[i][j] > maxlen:  # 随时更新最长长度和长度开始的位置
                        maxlen = dp[i][j]
                        maxindex = i - maxlen
                        # print('最长公共子串的长度是:%s' % maxlen)
                        # print('最长公共子串是:%s' % input_x[maxindex:maxindex + maxlen])
                else:
                    dp[i][j] = 0
        for dp_line in dp:
            print(dp_line)
        return maxlen, input_x[maxindex:maxindex + maxlen]
if __name__ == '__main__':
    lcs3 = LCS3()
    print(lcs3.lcs_dp('cabdec','cbdec'))

运行结果

[1, 0, 0, 0, 1]
[0, 0, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 0, 2, 0, 0]
[0, 0, 0, 3, 0]
[1, 0, 0, 0, 4]
bdec

Java

动态规划(懒得加上返回字符串了)

public static int lcs3(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int result = 0;     //记录最长公共子串长度  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                c[i][j] = c[i-1][j-1] + 1;  
                result = max(c[i][j], result);  
            } else {  
                c[i][j] = 0;  
            }  
        }  
    }  
    return result;  
    }