线性代数的中心问题是求解线性方程组。那什么是线性方程呢？所谓线性方程就是指未知量是一次幂的等式，它的一般形式是ax + by + … + cz = 0。也就是说线性方程组是由方程组成的，而这些方程的未知量都是一次幂。就如我们经常见到的y = ax + b就是线性方程，如果我们把y = ax + b画到二维的直角坐标系上，这个方程就是一条直线，这也就是为何叫做线性方程（这里的线性指的是直线，而非曲线）。
求解线性方程组我们主要讨论这样的问题：一个线性方程组是否有解，如果有解，有多少个解，如何求解；如果没有解的话，如何求近似解，以什么样的标准来求近似解；近似解是否唯一，如果不唯一的话，以什么样的标准选择近似解。
一个线性方程组是否可解等价于它的常数向量是否能够表示成各未知量系数向量的线性组合，举个例子：
一个线性方程组
它的常数向量是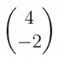
。
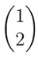
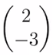
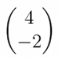
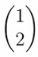
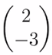
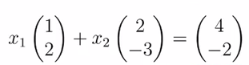第一节 行列式的基本概念和性质 一、基本概念 ①逆序 1,2和2,1是一对逆序 ②逆序数 1,2,3,5,4的逆序数为1;1,3,2,5,4逆序数为4; ③
线性代数 向量 物理向量 Prerequisite: 先决条件： [Defining a Vector using list][] [使用列表定义
线性代数 python Linear Algebra is a branch of mathematics that deals with large data by the
矩阵基础 矩阵是一个矩形排列的数表 最早人们为了解决方程组求解问题发明了矩阵 矩阵 由m x n个数aij(i、j都是从1到m、n的整数)排成的m行n列的数表
> 线性代数，基础知识，温故知新。 定义 向量： > 向量默认为列向量： x → = ( x 1 , x 2 , ⋯ , x n ) T = \[ x
线性代数的中心问题是求解线性方程组。那什么是线性方程呢？所谓线性方程就是指未知量是一次幂的等式，它的一般形式是ax + by + ... + cz = 0。也就是说线性方程组是
我会带着你远行
清疚
港控/mmm°
还没有评论，来说两句吧...