287. Find the Duplicate Number-蒲公英云

287. Find the Duplicate Number

Given an array nums containing n + 1 integers where each integer is
between 1 and n (inclusive), prove that at least one duplicate number
must exist. Assume that there is only one duplicate number, find the
duplicate one.

Note:
 - You must not modify the array (assume the array is read only). 
 - You must use only constant, O(1) extra space. 
 - Your runtime complexity should be less than O(n2). 
 - There is only one duplicate number in the array, but it could be repeated more than once.

题目描述：给一个n+1长度的数组，其中的数在1~n中，找到那个重复的元素

要求：不能修改数组
空间复杂度为O(1)
时间复杂度不能超过O(n^2)
数组中的元素可能不止重复一次

思路：其实这道题并不是多难，如果是使用之前的负数标记法，循环一遍数组，将每个元素值对应的数组元素取相反数，然后在之后的循环中进行判断，如果是相同元素值的话，那么所对应的数组元素应该是小于0的，但是这样不符合题目的要求

正是题目中的要求增加难度性，这里主要分析下最优解中的方法，空间复杂度为1，时间复杂度为n。这个方法叫做映射找环法

基本思想：将数组抽象为一条线和一个圆环，因为1～n 之间有n＋1个数，所以一定有重复数字出现，所以重复的数字即是圆环与线的交汇点。然后设置两个指针，一个快指针一次走两步，一个慢指针一次走一步。当两个指针第一次相遇时，令快指针回到原点（0）且也变成一次走一步，慢指针则继续前进，再次回合时即是线与圆环的交汇点。为什么一定会汇合？为什么汇合点就是重复数字？不要着急，我们先把Linked list circle问题弄明白。如图1所示，两个指针同时从直线起点开始，假设在x处第一次汇合，xo之间距离为x，那么快指针走过的路程为a+c+x,慢指针走过的路程为a+x，所以a+c+x=2(a+x),所以c＝a＋x，也就是SO之间的距离等于xo，所以令快指针从起点开始一次一步，慢指针从x开始，同时前进，则必会在O处相遇！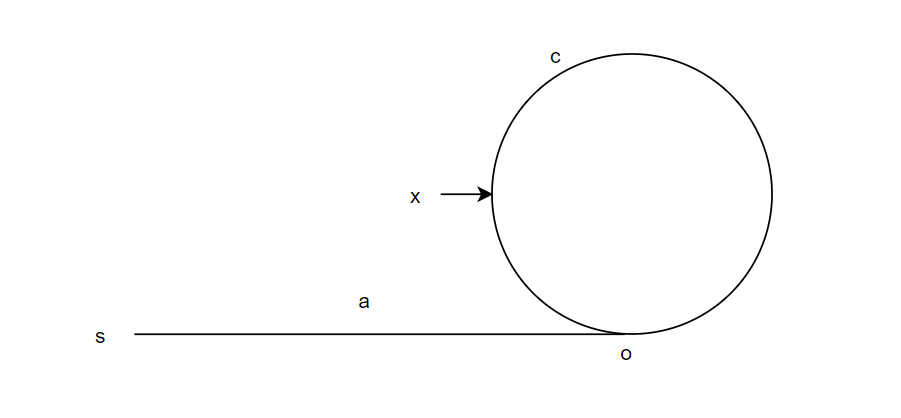
这里写图片描述

明白上面的之后，看下变型之后的，把数组抽象成线和圆环，举例来说，假设我们有一个数组是nums[]=[1，2，3，4，5，5，6，7]，pf代表快指针，ps代表慢指针，初始ps指向nums[0]，即1，pf指向nums[nums[0]]，即2,行动一次后，ps指向nums[1],即2，pf指向nums[nums[2]],即4，再动一次，ps指向nums[2],即3，pf则指向了nums[nums[4]],即5；可以发现pf一旦指向5后便不会再动，因为nums[5]一直为5，直到ps慢慢追上，然后令pf从头开始，ps一直在5处停留，最后定会相遇在这里，而这里就是重复数字。

换种说法，假设数组中没有重复，那我们可以做到这么一点，就是将数组的下标和1到n每一个数一对一的映射起来。比如数组是213,则映射关系为0->2, 1->1, 2->3。假设这个一对一映射关系是一个函数f(n)，其中n是下标，f(n)是映射到的数。如果我们从下标为0出发，根据这个函数计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推，直到下标超界。实际上可以产生一个类似链表一样的序列。比如在这个例子中有两个下标的序列，0->2->3。

但如果有重复的话，这中间就会产生多对一的映射，比如数组2131,则映射关系为0->2, {1，3}->1, 2->3。这样，我们推演的序列就一定会有环路了，这里下标的序列是0->2->3->1->1->1->1->…，而环的起点就是重复的数。

代码如下：

public int findDuplicate(int[] nums) {
        /*
        int rep = 0;
        for (int i = 0;i<nums.length; i++){
            int var = Math.abs(nums[i]) -1;
            if (nums[var] < 0){
                rep = Math.abs(var+1);
            }
            nums[var] = -nums[var];
        }
        return rep;
        */
        int slow = 0;
        int fast = 0;
        do{
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while(slow != fast);
        int find = 0;
        while(find != slow){
            slow = nums[slow];
            find = nums[find];
        }
        return find;
    }