Word Ladder

题目大意

给定一个起始字符串和一个目标字符串，现在将起始字符串按照特定的变换规则转换为目标字符串，求最少要进行多少次转换。转换规则为每次只能改变字符串中的一个字符，且每次转换后的字符串都要在给定的字符串集合中。

解题思路

参考：https://shenjie1993.gitbooks.io/leetcode-python/127%20Word%20Ladder.html
题目在2017年1月改动了，所以代码我也改动了。

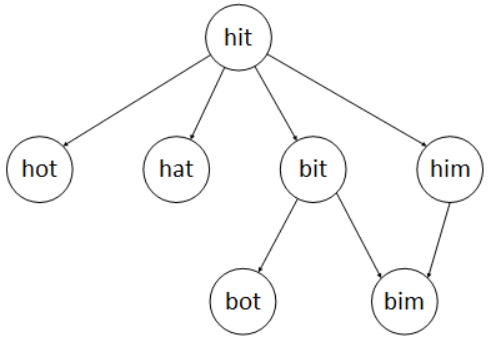
因为每次变换后的字符串都要在给定的字符串组中，所以每次变化的情况都是有限的。现在把变化过程做成一个树的结构，由某一个字符串变化而来的字符串就成为该字符串的子树。参看下图的例子，我们可以得到以下几点结论：

1.我们把起始字符串当成根节点，如果在变化过程中，某一个节点是目标字符串，那么就找到了一条变化路径。

2.节点所在的高度能够反映出变化到该节点时经历了几次变化，如hot在根节点的下一层，表示变化了一次，hut和bot在更下一层，表示变化了两次。
在树上层出现过的字符串没必要在下层再次出现，因为如果该字符串是转换过程中必须经过的中间字符串，那么应该挑选上层的该字符串继续进行变化，它的转换次数少。

3.如果上一层有多个字符串可以转换为下一层同一个字符串，那么只需要找到其中一个转换关系即可，如例子中的bit和him都可以转为bim，我们只需要知道有一条关系可以走到bim就可以了，没必要找到所有的转换关系，因为这样已经可以确定进行两次转换就能变为bim。

4.基于第3和第4点，当集合中的字符串在树中出现后，就可以把它从集合中删除。这样可以防止字符串不断地循环转化。

5.至此，这个问题就变为一个深度优先遍历问题，只需要依次遍历每一层的节点，如果在该层找到了目标字符串，只要返回相应的变化次数。如果到某一层树的节点无法继续向下延伸，且没有找到目标字符。

这里写图片描述

代码

wordList转换为set

不然LTE。最终668ms

class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordSet = set(wordList)
        cur_level = [beginWord]
        next_level = []
        depth = 1
        n = len(beginWord)  # 启示字符串长度
        while cur_level:
            for item in cur_level:
                if item == endWord:
                    return depth
                for i in range(n):
                    for c in 'abcdefghijklmnopqrstuvwxyz':
                        word = item[:i] + c + item[i + 1:]
                        if word in wordSet:
                            wordSet.remove(word)
                            next_level.append(word)
            # 树的下一层创建完毕
            depth += 1
            cur_level = next_level
            next_level = []
        return 0

cur_level也转换为set

按理说会更快一些，实际上并没有，但是再将next_level.append(word)变为next_level.append(str(word))后，却有提升至500ms。不甚理解。
PS:后经过试验，发现有时也会更差，看来leetcode时间果然不能信。

class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordSet = set(wordList)
        cur_level = set([beginWord])
        next_level = set()
        depth = 1
        n = len(beginWord)  # 启示字符串长度
        while cur_level:
            for item in cur_level:
                if item == endWord:
                    return depth
                for i in range(n):
                    for c in 'abcdefghijklmnopqrstuvwxyz':
                        word = item[:i] + c + item[i + 1:]
                        if word in wordSet:
                            print type(word), type(str(word))
                            wordSet.remove(word)
                            next_level.add(str(word))
            # 树的下一层创建完毕
            depth += 1
            cur_level = next_level
            next_level = set()
        return 0

Word Ladder II

题目大意

给定一个起始字符串和一个目标字符串，现在将起始字符串按照特定的变换规则转换为目标字符串，求所有转换次数最少的转换过程。转换规则为每次只能改变字符串中的一个字符，且每次转换后的字符串都要在给定的字符串集合中。

解题思路

为每次变换后的字符串都要在给定的字符串组中，所以每次变化的情况都是有限的。现在把变化过程做成一个树的结构，由某一个字符串变化而来的字符串就成为该字符串的子树。参看下图的例子，我们可以得到以下几点结论：

1.我们把起始字符串当成根节点，如果在变化过程中，某一个节点是目标字符串，那么就找到了一条变化路径。

2.节点所在的高度能够反映出变化到该节点时经历了几次变化，如hot在根节点的下一层，表示变化了一次，hut和bot在更下一层，表示变化了两次。

3.在树上层出现过的字符串没必要在下层再次出现，因为如果该字符串是转换过程中必须经过的中间字符串，那么应该挑选上层的该字符串继续进行变化，它的转换次数少。

4.如果上一层有多个字符串可以转换为下一层同一个字符串，那么只需要找到其中一个转换关系即可，如例子中的bit和him都可以转为bim，我们只需要知道有一条关系可以走到bim就可以了，没必要找到所有的转换关系，因为这样已经可以确定进行两次转换就能变为bim。

5.基于第3和第4点，当集合中的字符串在树中出现后，就可以把它从集合中删除。这样可以防止字符串不断地循环转化。

至此，这个问题就变为一个深度优先遍历问题，只需要依次遍历每一层的节点，如果在该层找到了目标字符串，只要返回相应的变化次数。如果到某一层树的节点无法继续向下延伸，且没有找到目标字符

代码

稍微有改动，应对改题目

class Solution(object):
    def findLadders(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: List[List[str]]
        """
        def bfs(front_level, end_level, is_forward, word_set, path_dic):
            if len(front_level) == 0:
                return False
            if len(front_level) > len(end_level):
                return bfs(end_level, front_level, not is_forward, word_set, path_dic)
            for word in (front_level | end_level):
                word_set.discard(word)
            next_level = set()
            done = False
            while front_level:
                word = front_level.pop()
                for c in 'abcdefghijklmnopqrstuvwxyz':
                    for i in range(len(word)):
                        new_word = word[:i] + c + word[i + 1:]
                        if new_word in end_level:
                            done = True
                            add_path(word, new_word, is_forward, path_dic)
                        else:
                            if new_word in word_set:
                                next_level.add(new_word)
                                add_path(word, new_word, is_forward, path_dic)
            return done or bfs(next_level, end_level, is_forward, word_set, path_dic)
        def add_path(word, new_word, is_forward, path_dic):
            if is_forward:
                path_dic[word] = path_dic.get(word, []) + [new_word]
            else:
                path_dic[new_word] = path_dic.get(new_word, []) + [word]
        def construct_path(word, end_word, path_dic, path, paths):
            if word == end_word:
                paths.append(path)
                return
            if word in path_dic:
                for item in path_dic[word]:
                    construct_path(item, end_word, path_dic, path + [item], paths)
        front_level, end_level = {beginWord}, {endWord}
        path_dic = {}
        wordSet = set(wordList)
        if endWord not in wordSet:
            return []
        bfs(front_level, end_level, True, wordSet, path_dic)
        path, paths = [beginWord], []
        # print path_dic
        construct_path(beginWord, endWord, path_dic, path, paths)
        return paths