【矩阵快速幂】Recurrences UVA

【矩阵快速幂】Recurrences UVA - 10870

Think:
1知识点：矩阵快速幂
2题意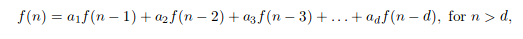：这里写图片描述
现输入d, n, m求解f(n)
注：f(i) = f(i) mod m;
3题意思考：
（１）：写出系数矩阵，矩阵快速幂求解
4反思：
（１）：注意系数矩阵与初始序列的对应关系
（２）：输入数据中每组测试数据换行相隔，而并不是要求在输出中每组测试数据以换行相隔，注意读题的严谨，注意细节

以下为Accepted代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL mod;
struct Matrix{
    LL v[24][24];
};
Matrix multiply(const Matrix &a, const Matrix &b, int Matrix_len);
Matrix matrix_pow(Matrix x, LL k, int Matrix_len);
LL rec[24];
int main(){
    int d, i;
    LL n;
    while(~scanf("%d %lld %lld", &d, &n, &mod) && (d || n || mod)){
        Matrix x;
        memset(x.v, 0, sizeof(x.v));
        for(i = 1; i <= d; i++){
            scanf("%lld", &x.v[1][i]);
            x.v[1][i] %= mod;
        }
        for(i = 1;i < d; i++){
            x.v[i+1][i] = 1;
        }
        for(i = d; i >= 1; i--){
   /*初始序列：[f(d)...f(1)]*/
            scanf("%lld", &rec[i]);
            rec[i] %= mod;
        }
        if(n <= d) printf("%lld\n", rec[d-n+1]%mod);
        else {
            Matrix y = matrix_pow(x, n-d, d);
            LL ans = 0;
            for(i = 1; i <= d; i++){
                ans += y.v[1][i]*rec[i]%mod;
                ans %= mod;
            }
            printf("%lld\n", ans);
        }
    }
    return 0;
}
Matrix multiply(const Matrix &a, const Matrix &b, int Matrix_len){
    Matrix tmp;
    memset(tmp.v, 0, sizeof(tmp.v));
    for(int i = 1; i <= Matrix_len; i++){
        for(int j = 1; j <= Matrix_len; j++){
            for(int k = 1; k <= Matrix_len; k++){
                tmp.v[i][j] += (a.v[i][k]*b.v[k][j]);
                tmp.v[i][j] %= mod;
            }
        }
    }
    return tmp;
}
Matrix matrix_pow(Matrix x, LL k, int Matrix_len){
    Matrix tmp;
    memset(tmp.v, 0, sizeof(tmp.v));
    for(int i = 1; i <= Matrix_len; i++)
        tmp.v[i][i] = 1;
    while(k){
        if(k & 1)
            tmp = multiply(tmp, x, Matrix_len);
        x = multiply(x, x, Matrix_len);
        k >>= 1;
    }
    return tmp;
}