leetcode 84. Largest Rectangle in Histogram 最大直方图 + DP +stack-蒲公英云

leetcode 84. Largest Rectangle in Histogram 最大直方图 + DP +stack

- 日理万妓 2022-06-08 02:26 218阅读 0赞

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

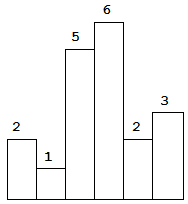
这里写图片描述
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

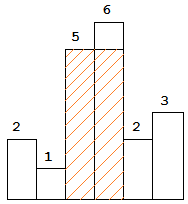
这里写图片描述
For example,
Given heights = [2,1,5,6,2,3],
return 10.

这道题和 leetcode 32. Longest Valid Parentheses 最长有效括号长度很类似，可以放到一起学习。

这道题最直接的方法就是暴力搜索了，从第一个方块开始，向前向后一直搜索到比它高度小的方块为止，然后更新最大面积，这种方法的时间复杂度是O(n^2)。

借助于stack这一数据结构，可以实现一个O(n)的算法，具体思路如下：stack中存储的是方块的下标索引号，如果当前方块的高度大于等于栈顶元素对应方块的高度，那么就将该方块的索引号进栈。否则（即当前方块高度更小时），则说明继续划分下去会产生镂空区域，因此我们将栈顶元素一次出栈，每次出栈时都计算一下以该栈顶元素为高度基准时，划分出的面积大小。

建议和leetcode 85. Maximal Rectangle 最大子矩阵一起学习，这道题是对本体做的一个很不错的拓展，很值得学习

代码如下：

import java.util.Stack;
/*
 * stack中存储的是方块的下标索引号，如果当前方块的高度大于等于栈顶元素对应方块的高度，
 * 那么就将该方块的索引号进栈。否则（即当前方块高度更小时），则说明继续划分下去会产生镂空区域，
 * 因此我们将栈顶元素一次出栈，每次出栈时都计算一下以该栈顶元素为高度基准时，划分出的面积大小。
 * 这样这个算法复杂度就降低到了O(n)，具体请看代码。
 * */
public class Solution 
{
    public int largestRectangleArea(int[] height) 
    {
        if(height==null || height.length<=0)
            return 0;
        int maxArea=0,i=0;
        Stack<Integer> stack=new Stack<>();
        while(i<height.length)
        {
            //要是可以保证升序序列就直接进栈
            if(stack.isEmpty() || height[stack.peek()] <= height[i])
                stack.push(i++);
            else 
            {
                /*
                 * 否者的话直接计算以height[pre]为高度的面积，为什么呢？
                 * 因为假如pre之前有比height[pre]要小的元素，那么pre早就出栈了，
                 * 所以可以计算以height[pre]为高度的面积，那么宽度是哪里呢？
                 * 首先起点是stack的top+1，因为height[pre]要比现在的top的height要大，
                 * 同时重点是i-1，因为height[pre]>height[i]
                 * */
                int pre=stack.pop();
                int width=stack.isEmpty()?(i-1)-0+1 : (i-1)-(stack.peek()+1)+1;
                maxArea=Math.max(maxArea, width * height[pre]);
            }
        }
        //其实到了这里i就是height.length
        while(stack.isEmpty()==false)
        {
            int pre=stack.pop();
            int width=stack.isEmpty()?(height.length-1)-0+1 : (height.length-1)-(stack.peek()+1)+1;
            maxArea=Math.max(maxArea, width * height[pre]);
        }
        return maxArea;
    }
}

下面是C++的做法，这道题很值得学习

代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
using namespace std;
class Solution 
{
public:
    int largestRectangleArea(vector<int>& hei) 
    {
        if (hei.size() <= 0)
            return 0;
        stack<int> index;
        int i = 0, maxArea = -1;
        while (i < hei.size())
        {
            if (index.empty() || hei[i] >= hei[index.top()])
                index.push(i++);
            else
            {
                int pre = index.top();
                index.pop();
                int width = index.empty() ? (i - 1) - 0 + 1 : (i - 1) - (index.top()+1) + 1;
                maxArea = max(maxArea, width*hei[pre]);
            }
        }
        while (index.empty() == false)
        {
            int pre = index.top();
            index.pop();
            int width = index.empty() ? (hei.size() - 1) - 0 + 1 : (hei.size() - 1) - (index.top() + 1) + 1;
            maxArea = max(maxArea, width*hei[pre]);
        }
        return maxArea;
    }
};